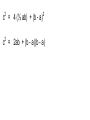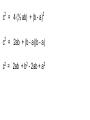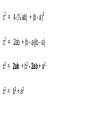* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Unit 2B Parallelograms - Clark Magnet High School
Survey
Document related concepts
Transcript
Unit 2B Parallelograms Day 5 Tuesday, Nov 8, 2016 Agenda 11/8/2016 1) Bulletin 2) Pythagorean Problems - what did you come up with? 3) Unit 2B Review Part 1 4) Unit 2B Review Part 2 5) Thursday Unit 2B test (45mins). Pythagorean theorem problem A. We know that x + y + z = 180° since they form a straight angle (line). We know that the four right triangles are congruent so they can be labelled with the angles x and y and the right angle. So since the sum of the 3 angles in a triangle is always 180°, we know that x + y = 90° And so by substitution (90°) + y = 180°, or y= 90° A. continued. So the inside quadrilateral has 4 congruent sides and 4 right angles, so it must be a square. B. 1) Determine the area of the large square using the length of its sides. Area = length x width A = (a + b)(a + b) A = a2 + 2ab + b2 B. 2) Determine the area of the large square as the sum of the areas of the four triangles and the inside square. Area = 4 (½ ab) + c(c) A = 2ab + c2 C. Use results of Parts A and B to demonstrate that the Pythagorean theorem is true. From 1 and 2 above we have 2 equations for the area of the same large square. A = 2ab + c2 A = a2 + 2ab + b2 So by substitution 2ab + c2 = a2 + 2ab + b2 C. Use results of Parts A and B to demonstrate that the Pythagorean theorem is true. So by substitution 2ab + c2 = a2 + 2ab + b2 If we Subtract 2ab from both sides of this equation We get: c 2 = a2 + b2 C. We get: c 2 = a2 + b2 c b a Which is how we write the Pythagorean theorem for a right triangle labelled as in the original diagram. Possible extension for class activity. How did you finish labelling the diagram to help you write an alternative proof of the Pythagorean theorem? White board c2 = 4 (½ ab) + (b - a)2 c2 = 2ab + (b - a)(b - a) c2 = 4 (½ ab) + (b - a)2 c2 = 2ab + (b - a)(b - a) c2 = 2ab + b2 - 2ab + a2 c2 = 4 (½ ab) + (b - a)2 c2 = 2ab + (b - a)(b - a) c2 = 2ab + b2 - 2ab + a2 c2 = b2 + a2 Fill in the blanks with sometimes, always or never. State your reasons. 1. A square is always a rhombus. Reasons: A rhombus is a quadrilateral with four congruent sides and diagonals that are perpendicular and bisect each other (and bisect a pair of opposite angles). A square has all these same properties, so it can always be classified as a rhombus. (pg 351) Fill in the blanks with sometimes, always or never. State your reasons. 2. The diagonals of a parallelogram are sometimes congruent. Reasons: Fill in the blanks with sometimes, always or never. State your reasons. 2. The diagonals of a parallelogram are sometimes congruent. Reasons: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. If a parallelogram is a rectangle then the diagonals are congruent. Parallelograms are only rectangles sometimes. Fill in the blanks with sometimes, always or never. State your reasons. 3. A quadrilateral with (only) one pair of congruent sides and (different) one pair of parallel sides is never a parallelogram. Reasons: Would be an isosceles trapezoid. However, it might be a parallelogram if one pair of opposites sides was parallel and that pair were also congruent. If one pair of opposite sides of a quadrilateral is both parallel and congruent, then the quadrilateral is a parallelogram. P 334 Fill in the blanks with sometimes, always or never. State your reasons. 4. The diagonals of a parallelogram always bisect each other. p 335 Reasons: This is one of the theorems we use when we want to prove a quadrilateral is a parallelogram. Fill in the blanks with sometimes, always or never. State your reasons. 5. A quadrilateral with 4 congruent sides is sometimes a square. Reasons: A rhombus is also a quadrilateral with 4 congruent sides. 6. Give 2 facts about a rectangle that are not true for all parallelograms. a) b) HINT: USE THE TABLE ON PAGE 62 OF YOUR WORKBOOK TO WRITE SOME CORRECT RESPONSES THAT YOU WILL BE ABLE TO REMEMBER. 7. Give 2 facts about a rhombus that are not true for all parallelograms. a) b) Use the table on page 62 to help you find facts that are true for rhombi but not for all parallelograms. Complete these theorems: 8. If one pair of opposite sides of a quadrilateral are both ___________ and ___________, then it is a parallelogram. 9. Each pair of base angles of a(n) ____________ are congruent. Complete these theorems: 8. If one pair of opposite sides of a quadrilateral are both parallel and congruent, then it is a parallelogram. 9. Each pair of base angles of a(n) isosceles trapezoid are congruent. 10. Quadrilaterals with diagonals that are perpendicular. 10. Quadrilaterals with diagonals that are perpendicular. kite rhombus square 11. Given WXYZ is a parallelogram, and angle XWZ is congruent to angle YRZ Prove: Line segment YR is congruent to line segment XW. Draw the given information on the diagram first. Unit 2B Review Part 2 For Additional practice see the Mid-Chapter Quiz on page 347 of your textbook Questions 6, 7, 8, 10, 11, 14, 15. Homework Continue to Practice for the 2B test on Thursday. I will post some worked answers in the google classroom tomorrow after school.