* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download hilgrove-segment-lengths-and-chord-properties
Euler angles wikipedia , lookup
History of geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Multilateration wikipedia , lookup
Euclidean geometry wikipedia , lookup
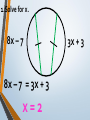
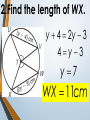
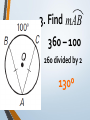
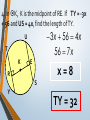
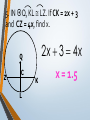
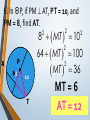
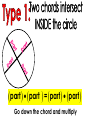
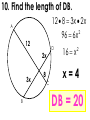
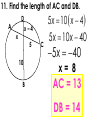
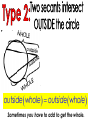
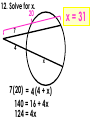
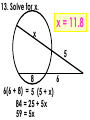
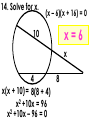
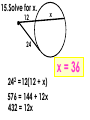
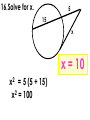
An Affirmation Please read the following and consider yourself in it. I am capable of learning. I can accomplish mathematical tasks. I am ultimately responsible for my learning. GSE Geometry: Arc, Angles, and Area. Objectives SWBAT understand that ALL circles are similar IOT find circumference and areas of circles SWBAT apply the relationship between central, inscribed, and circumscribed angles IOT solve for unknown quantities in a circle. SWBAT apply relationships among inscribed angles, radii, chords, tangents and secants IOT solve for unknown quantities in a circle. SWBAT define radian measure and derive the formula for area of a sector IOT solve circle problems. Chord Properties and Segments Lengths in Circles If two chords are congruent, then their corresponding arcs are congruent. 1.Solve for x. 8x – 7 8x – 7 = 3x + 3 x=2 3x + 3 2.Find the length of WX. y 4 2y 3 4y3 y 7 WX 11cm 3. Find mAB 360 – 100 260 divided by 2 130º If two chords are congruent, then they are equidistant from the center. 4. In K, K is the midpoint of RE. If TY = -3x + 56 and US = 4x, find the length of TY. 3 x 56 4 x 56 7x U T K E x=8 R S Y TY = 32 If a diameter is perpendicular to a chord, then it also bisects the chord. This results in congruent arcs too. Sometimes, this creates a right triangle & you’ll use Pythagorean Theorem. 5. IN Q, KL LZ. If CK = 2x + 3 and CZ = 4x, find x. 2x 3 4x Q Z C L K x = 1.5 6. In P, if PM AT, PT = 10, and PM = 8, find AT. 8 MT 10 2 2 2 64 MT 100 2 MT 36 2 P A M8 10 T MT = 6 AT = 12 7. Find the length of CE BD is a radius. CB is a radius. What is the length of the radius? 25 2 2 20 x 25 x 15 Now double it to find CE. 25 x 2 30 8.Find the length of LN. MK and KL are radii. 2 2 14 x 50 2 x 48 x 50 Now double it to find LN. LN = 96 Segment Lengths in Circles part part = part part Go down the chord and multiply 9. Solve for x. 9 2 6x 18 6x x=3 9 x 6 2 10. Find the length of DB. 12 8 3 x 2 x 2 96 6x A 12 D 2x 3x B 8 C 16 x 2 x=4 DB = 20 11. Find the length of AC and DB. A x 5 x 10 x 4 D x–4 5 10 B C 5 x 10 x 40 5 x 40 x= 8 AC = 13 DB = 14 outside whole outside whole Sometimes you have to add to get the whole. 12. Solve for x. x = 31 20 7 4 x 7(20) = 4 (4 + x) 140 = 16 + 4x 124 = 4x 13. Solve for x. x x = 11.8 5 8 6 6(6 + 8) = 5 (5 + x) 84 = 25 + 5x 59 = 5x 14. Solve for x. (x – 6)(x + 16) = 0 x=6 10 x 4 x(x + 10) = 8(8 + 4) 2 x +10x = 96 x2 +10x – 96 = 0 8 tan = outside whole 2 15.Solve for x. 12 x 24 242 =12(12 + x) 576 = 144 + 12x 432 = 12x x = 36 16.Solve for x. 5 15 x x = 10 x2 = 5 (5 + 15) x2 = 100