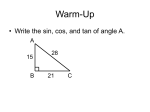
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download MATH 120-04 - CSUSB Math Department
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Analytic geometry wikipedia , lookup
Conic section wikipedia , lookup
Metric tensor wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Signed graph wikipedia , lookup
Line (geometry) wikipedia , lookup
CR manifold wikipedia , lookup
120.htm MATH 120-04: Pre-Calculus Mathematics (43416) JB-138, TuTh 4 - 5:50 PM SYLLABUS Spring 2013 John Sarli JB-326 [email protected] 909-537-5374 Office Hours: TuTh 11-1 PM, or by appt. Text: Swokowski/Cole custom edition for CSUSB College Algebra & Trig Math Prerequisites: MATH 110 or satisfactory score on the ELM This a course in the fundamentals of pre-calculus mathematics. The main emphasis is on the theory and applications of trigonometric functions, but we will also cover topics in analytic geometry, mathematical induction and the binomial theorem. In particular, we will cover the following sections of the text in this order: Chapters 6,7,8; Chapter 10, sections 4 and 5. We may cover material from Chapters 11, sections 1,2,3 if time permits. Grading will be based on two midterm exams, a cumulative final exam, four graded assignments, and a project, weighted as follows: First Midterm (10%), Second Midterm (20%), Final Exam (40%), Graded Assignments (20%), Project (10%). To reinforce written communication skills the Graded Assignment solutions should be clearly presented, either in a "bluebook" or sent to me as a .pdf file (do not scan in handwritten work). The graded assignments will be chosen to encourage understanding of a variety of applications, often within social and historical contexts, of developments within and related to the natural sciences. To reinforce the importance of clear presentation I will occasionally take some class time for you to complete an MDTP Written Response item, which I will score on a to scale and return to you by the next class. These scores do not affect your course grade; they serve to provide you with some feedback on your presentation skills. The Project must be on some aspect of the mathematics of conic sections, the basics of which are covered in Chapter 11. Details will be given as we progress but the purpose of the project is to have you present, in your own words, a topic that uses conic sections in some context. Although there is no attendance requirement for this class, you must complete the CSU/UC Mathematics Diagnostic Testing Project CR test within the first two weeks of the course (by April 16). Go to mdtp.ucsd.edu and scroll down to MDTP Web Based Tests. Select the CR test. The items will appear one at a time. You can either print the results or send them to me electronically. The results do not affect your course grade in any way, but failure to complete this requirement will subject you to disenrollment. Although you are encouraged to learn the use of a calculator with graphing capability, exams are conducted in class without calculators. A list of Suggested Exercises will be provided prior to the start of each chapter and the exams will be closely modeled on these. After computing your total scores weighted according to the percentages above, course grades will be assigned as follows: 120.htm[6/6/2013 1:02:31 PM] 120.htm Notes 1) Some important dates: April 2 - First day of class April 22 - Last day to submit adds/drops/audits/CBE April 18 - First exam May 16 - Second Exam June 6 - Last day of class Tuesday, June 11- Final Exam 2) Notes for the lectures and associated topics will appear on my website www.math.csusb.edu/faculty/sarli/ along with this syllabus. 3) Mid-term exam dates are subject to change. Due dates for the graded exercises will be set as we approach the end of each chapter of the text. The Project is due on June 6 - no exceptions. 4) This course satisfies the requirement of Basic Skills Category A.3 in the CSUSB General Education Program. Please refer to the Academic Regulations and Policies section of your current bulletin for information regarding add/drop procedures and consequences of academic dishonesty. 5) If you are in need of an accommodation for a disability in order to participate in this class, please let me know ASAP and also contact Services to Students with Disabilities at UH-183, (909)537-5238. MATH 120-04: Chapter 6 (Swokowski/Cole, CSUSB edition) . The following Suggested Exercises are not to be handed in but are a representative sample of techniques required for basic mastery. 120.htm[6/6/2013 1:02:31 PM] 120.htm 6.1 (pages 375-377): 6.2 (pages 390-393): 6.3 (pages 407-410): 6.4 (pages 416-417): 6.5 (pages 426-429): 6.6 (pages 435-437): 6.7 (pages 443-449): First Graded Assignment To reinforce written communication skills the Graded Assignment solutions should be clearly presented in a "bluebook" or provided in .pdf format. The assignments are chosen to encourage understanding of a variety of applications, often within social and historical contexts, of developments within and related to the natural sciences. Late papers will not be graded. First Graded Assignment. Do any one of the following: Due Tuesday, April 30. 6.1: (Note: "reading of the data occurs at a constant rate" means linear speed remains constant) 6.3: 6.4: 6.5: 6.6: 6.7: or or Review Exercises (pages 449-455): or or Notes on Chapter 6 Central angles Central angles An angle whose vertex is at the center of a circle is called central. The angle is often referred to by its measure circle at points and then the circle is divided into two arcs. Normally, when we refer to the arc along the circle in the counterclockwise direction from subtends Let to . If the rays of intersect the we mean the arc determined by moving , but context often determines which of the two arcs we mean. We say that the arc . be the radius of the circle. If the length of arc 120.htm[6/6/2013 1:02:31 PM] is equal to then the measure of is one radian. Since the circumference of the 120.htm circle is it follows that which allows us to convert easily between radian and degree measure. Note that the degree symbol must always follow degree measure, but, by convention, we normally suppress the word "radian" when using radian measure. If it is not suppressed, it is often denoted by . Thus Arc length and sectors We will use radian measure unless degree measure is specifically indicated. Again, since the circumference of the circle is proportionality that if is the length of an arc that subtends the central angle By similar reasoning, since the area of the circle is determined by , it follows by then , it follows by proportionality that if is the area of the circular sector then Angular and linear speed The formula for arc length allows us to relate the linear speed of a point on the circumference of a circular object that is rotating at a constant rate about its center to the angular speed of the object itself. The linear speed is the distance that so it must be measured in units of distance/time, for example, cm/sec. The angular speed time by a ray from the center through travels per unit of time of the object is the angle generated in one unit of , thus The letter is used generically for angular speed though other letters may be used in various contexts. Note that it is measured in units of angle-measure/time, for example, rad/sec. Angular speed does not depend on the radius of the object but linear speed does; in particular, note that because . Angles in standard position in the plane An angle with vertex in the Cartesian plane is in standard position if one of its rays is the positive -axis (horizontal axis). We adopt an orientation on such angles by designating the positive -axis ray as the initial ray and the other ray as the terminal ray. (What does it mean if these rays coincide?) Thus we adopt a dynamic viewpoint: the measure of this angle is determined by how we move from the initial ray to the terminal ray. By convention, if the movement is counterclockwise the measure is a positive number, whereas it is a negative number if we move clockwise. We can measure either in degrees or radians, but we will find radians easier to use when we work with functions. Note that neither the positive nor negative measure of an angle is unique. For example, the angle whose terminal ray is the positive -axis could have measure , etc., or it could have measure 120.htm[6/6/2013 1:02:31 PM] , etc., but any measure for this angle is of the form 120.htm where is an integer. Fundamental trigonometric functions The equation describes the circle of radius circle. Then we can define real-valued functions of trigonometric functions. For example, let centered at in the Cartesian plane. Let be a point on this that are useful in a wide variety of applications. These are known as the fundamental Since the functions and satisfy a special property called the Pythagorean identity. We will give them special names once we interpret their definitions in the more familiar context of functions on the real number line. To accomplish this, first note that if then and real number to the point let . Thus it simplifies our work if the circle we use is the unit circle. The functions . We can associate a real number to as follows. Given as the odometer reading on a car as it drives from to each assign a , determine the terminal ray that passes through be the radian measure of this standard angle. Note, from the formula for arc length, that unit circle. Think of and is just the distance from to along the , where the reading is positive if the car drives counterclockwise around the circle and negative if it drives clockwise. For example, if the smallest positive measure of the standard angle is . We have and now we can write . Similarly, . Apparently, the functions and measuring the oriented horizontal and vertical distances from the center of the circular track as the car drives along it. Note also that for any integer . Thus the functions and . Now are just are not one-to-one; in fact, infinitely many inputs produce the same output. We now have two equivalent ways of describing the functions and . We originally defined them as functions whose inputs are points in the plane, and then noted that these functions are constant on the terminal ray through . This allowed us to define and as functions on the entire real line by associating that terminal ray with its radian measure. These functions are of fundamental importance. We will see that they generalize the trigonometry of right triangles. Thus we give them familiar names and use them to define the other four fundamental trigonometric functions In practice, we determine the values of the functions for a particular value of point on the unit circle by travelling from 120.htm[6/6/2013 1:02:31 PM] through the distance . Then by the following thought process: Given , locate the unique 120.htm Domains, ranges, and periods Since we now have special names and designations for the fundamental trigonometric functions (cosine, sine, tangent, cotangent, secant, or if then the input cosecant) we can use a generic letter, such as , to stand for any of them in context. Note that if for can be any real number, and the output can be any number in the closed interval sine functions is and the range is . Thus the domain of the fundamental cosine or . These functions are periodic, that is, there is a number such that ; in fact, the smallest positive with this property is , so we say that the period of these functions is . With just these few observations we can visualize the graphs of these functions, at least qualitatively. Our goal is to analyze their behavior in more detail, which will then allow us to analyze the other four functions in detail. Now suppose or . Since the secant function is the reciprocal of the cosine function it is defined everywhere except where the cosine function is zero. Thus the domain of the secant function is and its range is because . Similarly, the range of the cosecant function is also for any integer . Qualitatively we can now visualize the graphs of , whereas its domain is and vertical asymptotes at the values missing from their domains, and by noting that these functions are also periodic with period by picturing . Finally, suppose or . These two functions are reciprocals of each other. Since the domain of the tangent function will be the same as the domain of the secant function, whereas the domain of the cotangent function will be the same as the domain of the cosecant function. Since the sine and cosine functions cannot simultaneously be zero and their ranges are bounded, we conclude that the range of the tangent function is , as is the range of the cotangent function. Again we have a qualitative picture of their graphs, with vertical asymptotes at the values missing from their domains. These two functions are also periodic, with the same period, but that period is not . As the terminal ray determined by sequence moves through the four quadrants of the plane the signs for the outputs of the cosine function follow the whereas the signs for the outputs of the sine function follow the sequence Consequently and so Thus (being the smallest positive number for which periodicity happens) is the period of these two functions. The shape of their graphs repeats twice as frequently as does the shape of the graphs of the other four fundamental trigonometric functions. 120.htm[6/6/2013 1:02:31 PM] 120.htm Pythagorean identities We have seen that the ordered pair where, as usual, the symbol is a point on the unit circle . This fact gives us the first Pythagorean identity means that the equation is true for all values of for which the functions can be evaluated. Since the domain of the cosine function is , as is the domain of the sine function, this equation is an identity for all values of . Two other Pythagorean identities are obtained for the other fundamental trigonometric functions Note that the first equation is an identity for all values of except multiples of except odd multiples of and the second equation is an identity for all values of . Using the Pythagorean identities we can derive most other identities that are useful in calculus. Even and odd functions In a prior course you may have seen the following definitions: A function is called even provided for all in its domain. A function is called odd provided for all in its domain. Using generic Cartesian variables, note then that the functions symmetric about the -axis), whereas , and , are even functions (their graphs are , and are odd functions (their graphs are symmetric about the origin). To see that these functions are even or odd as claimed, choose any value in the domain and locate the point on the unit circle corresponding to this value. Now locate the point corresponding to , which is antipodal to the first point. If the value of the function is the same for both points then the function is even, but if the values have opposite signs then the function is odd. As we consider trigonometric functions that are not fundamental it is important to realize that, in general, they will be neither even nor odd. At this point you should evaluate your understanding by working Suggested Exercises from sections 6.1 through 6.4. Functions of the form and In practice, trigonometric functions are rarely used in just their fundamental forms. In order to understand general trigonometric functions, we begin with alterations of the fundamental functions obtained from linear changes to the independent and dependent variables. We illustrate these for the sine and cosine functions, but the same principles apply to any of the fundamental functions. Alterations of fundamental functions are easily described in terms of graphs. Linear changes to the dependent variable result in vertical . we can changes to the graph. We examine these first since they do not change the domain of the original function. Consider a graph create a new function by adding a constant If to the output of this function, resulting in the graph this graph is obtained by translating the graph translating the graph downward by units. If units. This is the simplest of the linear alterations. The other linear change to the dependent variable is of the form 120.htm[6/6/2013 1:02:31 PM] upward by the graph is obtained by 120.htm where, again, is a constant. The graph ) vertically. In addition, if follows. Start with the graph Next, produce the graph and then the graph and finally the graph 120.htm[6/6/2013 1:02:31 PM] is obtained by stretching the graph the graph is reflected in the (if ) or compressing it (if -axis. As an example, we construct the graph as 120.htm Note that the domain of is still , but the range of this function is . Now consider linear changes to the independent variable. These will result in horizontal changes to the graph. For any constant the graph Since we have added if to the input variable this graph is obtained from the graph and to the right if . A good way to remember this is to imagine a particular , so the graph if by translating it horizontally has an -intercept at -intercept for , which is to the left of , consider units: to the left . We have if and to the right of . For example, This graph has its smallest positive -intercept at because has its smallest positive -intercept at . The other linear change to the dependent variable is of the form for some constant , and this results in a horizontal stretch or compression of the graph graph is compressed, whereas the graph is stretched if 120.htm[6/6/2013 1:02:31 PM] . Note, however, that if . A good way to remember this is to think of the function the , whose graph 120.htm is a straight line of slope . The function is a straight line of slope horizontally. Similarly, the graph of is reflected in the , which can be thought of as the line of slope can be thought of as the line of slope compressed stretched horizontally. (Note that if -axis. For the trigonometric functions we will see that we can always work with the case the graph . For example, , because the fundamental sine function is odd, so its graph is just the reflection of in the -axis.) It is important to remember that stretch and compression are in relation to the vertical axis, which is different from dilation about a point. Thus, the point where a horizontal line intersects is twice as far from the -axis as the point where this line intersects . from the graph How do we obtain the graph . Note that the graph graph is obtained by translating the graph is obtained from the graph illustration, we construct the graph and then, since ? We have , where , as described above. Then the by stretching or compressing as determined by , compress this graph to obtain see what happens to the graph , when the input variable was unaltered. We let . To do this, we first undo the translation part and then undo the stretch/compression part 120.htm[6/6/2013 1:02:31 PM] . As an as follows. First obtain the graph A good way to remember this procedure is to remind yourself that you are making changes to the input variable: is, we invert the function and and proceed to find . We want to in terms of , that 120.htm The actions we take to invert by are precisely the actions we apply to , horizontally: translate by and then multiply . that is useful in applications. Since There is another approach to obtaining the graph so now we have , but this time with and obtained from by stretching or compressing as determined by the graph by translating as determined by . Now the graph . Then the graph . Again, we construct the graph First obtain the graph which has an -intercept at which has an -intercept at 120.htm[6/6/2013 1:02:31 PM] , and then translate this graph . Again, units to the left to obtain we can write is is obtained from . 120.htm the actions we take to invert translate by are precisely the actions we apply to , horizontally: multiply by and then . Amplitude, frequency and phase shift The second procedure, above, for obtaining the graph introduces an important parameter, called phase shift, used in the description of harmonic motion. Before we define it precisely we introduce some terminology useful in the description of wave phenomena. The fundamental sine and cosine functions, as well as their linear alterations, have ranges that are closed intervals. This allows us to define the amplitude of the wave shapes defined by their graphs. For the functions we define the amplitude to be the non-negative number . Note that the amplitude is not the same thing as the range of the function, though it is related to it. The actual range of the above functions is the closed interval For example, the range of the function is the interval whereas its amplitude is . The amplitude measures the height of the wave above (or the depth of the wave below) its horizontal center line. For the function above, note that the period is of the function , that is, for all . For any fundamental trigonometric function with period , we define the period to be the positive number (This definition agrees with the behavior of the graphs of these functions, and obviously generalizes our use of the word in the case of the fundamental trigonometric functions.) We define the phase shift of this function to be 120.htm[6/6/2013 1:02:31 PM] 120.htm which you can remember as the final step in isolating the input variable when we write For the graph above, note that . At this point you should evaluate your understanding by working Suggested Exercises from sections 6.1 through 6.6. For the first exam, focus in particular on the following: Geometric relations among central angle, radius, arc length, and area of sector. Angular speed and linear speed, in correct units. Determining values of the fundamental trigonometric functions given a terminal ray in standard position or a point on that ray. Expressing fundamental trigonometric functions in terms of each other. Constructing graphs of linear alterations to the dependent variable of fundamental trigonometric functions, and determining: Domain Range Amplitude Period Intercepts Asymptotes Background for the project: Conics A circle is an example of a conic. Conics were described in detail prior to Euclid's work (primarily by Menaechmus), but the development was based on their properties as sections of cones in three dimensions. This approach was reconciled with their descriptions as plane curves (loci) by later mathematicians such as Apollonius of Perga and, about 600 years after Euclid, by Pappus of Alexandria, who created the foundations of what would eventually become analytic geometry. Euclid understood the importance of conic curves and asserts the existence of circles in his postulates as loci of points equidistant from a given point. Numerous manifestations of conics occur throughout history since they are essential to the understanding of many physical phenomena. Most of these derive from the following locus description that dates from antiquity. A conic is the locus of a points whose distance from a given point is constant. times its distance from a given line, where is a non-negative The given point and line are called a focus and its corresponding directrix. The constant is called the eccentricity of the conic. Without coordinate geometry, mathematicians such as Apollonius used synthetic techniques to describe the conics that would correspond to various values of . In pre-calculus our approach uses analytic geometry, the geometry of the coordinate plane. Using analytic geometry we can reduce the lengthy synthetic development to a few basic equations. This shows the power of modern notation. You should make your own drawing to represent the following argument. First, let to be the given focus and let , so the condition for . For any point let be the point on the directrix closest to be on the conic is Now consider the line through 120.htm[6/6/2013 1:02:31 PM] be the point on the directrix closest to parallel to the directrix. Since this line is perpendicular to the line , by symmetry there must be two 120.htm points, and , on this line that are also on the conic. Let directrix closest to be the length of segment (hence also of ). Then, if is the point on the we have Next, for any point on the conic let Let be the measure of angle But so . Then . Then We conclude that an equation that offers a lot of information. For example, we required that the focus is constant and so the conic is the circle centered at . If then , that is, the distance between with radius . Where is the directrix in this case? Since and the only way for to hold is for to be infinitely large. We say that the directrix is the "line at infinity" and use projective geometry to make this idea precise. Circles, then, are conics with zero eccentricity, and any line through the center is a line of symmetry. The angle locates symmetric about the line relative to the line . When , and we can assume we have . Since , whereas, if it follows that the conic is , this line intersects the conic again when , whereby . When the conic is called a parabola. A point where the conic intersects its line of symmetry is called a vertex. Thus, a parabola has a single vertex and all other conics, except circles, have exactly two vertices. Since a circle does not have a unique line of symmetry we generally do not think of its points as vertices. Because of this extra symmetry, it was believed for centuries that the motions of celestial bodies must be perfect circles in all cases. If note that is finite and positive for all values of is therefore a type of ellipse. If note that is positive if is on the ray through that is opposite the ray determined by that such a conic has two separate branches. Exercise. Let be such that is produced by , so the conic is a closed oval-shaped curve, which we call an ellipse. The circle . If . A conic with . Show that If we obtain 120.htm[6/6/2013 1:02:31 PM] is a negative number; this means that is called a hyperbola. The fact that changes sign means produces one branch of the hyperbola and that the other branch . . Let We can obtain Cartesian equations for conics from the relation we have then and is the -coordinate of . Thus and let be on the positive -axis. With 120.htm as the equation for the parabola. Exercise. How does the value of let If and let affect the shape of the parabola? . Exercise. Show that the Cartesian equation for the conic is Application: Harmonic Motion Functions of the form describe many physical measurements that vary with time . When such functions describe harmonic motion by giving the position of a point moving on a coordinate line relative to the origin. In this context it is common to write with , so the amplitude of the motion is , the period is , and the phase shift is . Since the motion is along a coordinate line it is also common in practical applications to set the origin so that , and in case the phenomenon is referred to as simple harmonic motion (SHM). The amplitude, then, is the maximum distance from the origin that the point reaches, the period is the time required for one complete oscillation, and the frequency , being the reciprocal of the period, is the number of oscillations per unit time. (Note the analogy with our use of for angular speed.) SHM applies to many physical systems, such as a mass attached to a spring that is set to move horizontally or vertically only by the force from an initial stretch or compression of the spring. Generally, the resting position of the mass in the absence of any stretch or compression of the spring is taken as the origin of the line along which the mass will move. That is, the values of such that are the times when the mass is at this origin position. Note that origin refers to the physical position of the mass, not the beginning of the motion. is not necessarily . In fact it will often be some other number: typically positive if the clock starts with the spring in a stretched That is, position, negative if it starts in a compressed position. As an example, consider a mass hanging vertically on a spring attached overhead. Designate the rest position (equilibrium) of the hanging mass as on the vertical line. Now compress the mass upward through cm and then release it at time . Assume the future positions of the mass are described by SHM and measure the time it takes for the mass to return to its initial compress position. Model this position as a function of assuming the time measured to complete one oscillation is To find the function we interpret the given information: In order to apply the first condition we must have The second condition yields 120.htm[6/6/2013 1:02:31 PM] seconds. . So the assumption of SHM yields , for otherwise . The implies . 120.htm With this function we can predict the motion of the mass. In particular, the frequency is as cycles/second, and the amplitude is occurs at times of a full oscillation per second, sometimes written cm. If we want to know when the mass will be at the equilibrium position we set . This such that that is, where because time is moving forward from . In particular, the first time the mass reaches the equilibrium position is seconds after it is released, when the mass is descending. It next reaches this position the length of time between two successive equilibrium positions is after it is released, when it is ascending. So, in general, seconds, precisely half the period. Since SHM does not model phase shift we need a slightly more sophisticated model to take this phenomenon into account. We now want to consider functions of the form We will see that phase shift can be analyzed using some basic identities that we will derive, as usual, from the geometry of the unit circle. This analysis will explain how phase shift occurs in simple physical systems. The presence of a non-zero phase shift means that the input to the . Thus it would help to understand how trigonometric functions behave in general trigonometric function involves a sum of terms, say when the input is of this form. A natural question is whether the output can be expressed in terms of fundamental trigonometric functions of the terms individually. This question is the key to the analysis of oscillatory phenomena, from springs to signal analysis. To answer it we return to the unit circle to develop identities for unit circle and find the length of the chord and . Locate the points and on the . Using the distance formula, the square of this length is However, the chord subtends the central angle Pythagorean Theorem we find that , and is the base of the isosceles triangle , with legs of length . Using the Equating these two expressions we find since is an even function. Since Note also that the graph of the function Therefore, and so 120.htm[6/6/2013 1:02:31 PM] is an odd function, replacing is obtained by translating the graph of with in the above identity yields to the right by . However, . Thus 120.htm These identities allow us to interpret phase shift in harmonic motion as follows: In other words, harmonic motion with amplitude motions, of equal frequencies, with amplitudes that exhibits phase shift can be interpreted as the superposition of two simple harmonic and such that This observation has practical applications when we consider the superposition of two SHMs with equal frequencies. For example, let a sum of two SHMs with different amplitudes but equal frequency Then and . Let . Since a single sine wave with phase shift . Alternatively, let Then again , so we can write the function as but now we can rewrite this function as a single cosine wave with phase shift . The superposition of two fundamental functions has produced a single wave that exhibits phase shift. The graph below shows this function as a sum of the two fundamental waves (dashed). 120.htm[6/6/2013 1:02:31 PM] 120.htm Theorem. Let and , with . Then . Alternatively, , where , where and . Note that the choice of in the above theorem is determined by . In applications, the value of is called an initial condition. As a corollary to this theorem, we can also obtain a general superposition law that allows us to add phase-shifted waves. , let and . Then Corollary. If Alternatively, Exercise. Suppose and . What relation between produces the smallest possible amplitude for and produces the largest possible amplitude for ? What relation between ? Give an example of each case. The following Suggested Exercises are not to be handed in but are a representative sample of techniques required for basic mastery. Chapter 7 Suggested Exercises (Swokowski/Cole, CSUSB edition) 120.htm[6/6/2013 1:02:31 PM] 120.htm 7.1 (pages 464-466): 7.2 (pages 476-479): 7.3 (pages 487-490): 7.4 (pages 496-499): 7.5 (pages 503-504): 7.6 (pages 515-519): Second Graded Assignment: Due May 16 To reinforce written communication skills the Graded Assignment solutions should be clearly presented in a "bluebook" or provided in .pdf format. Do not send electronic scan of handwritten work. The assignments are chosen to encourage understanding of a variety of applications, often within social and historical contexts, of developments within and related to the natural sciences. Late papers will not be graded. Second Graded Assignment. Do any one of the following: (considered one problem) Page 489: Page 490: (considered one problem) Page 498: Page 504: Page 518: Page 520: Trigonometric Equations and Identities An identity is a mathematical equation which is satisfied by all values in the domains of the functions that appear in the equation. For example, is an identity for all values of for which and values of the variables does equality hold? For example, is not an identity, so we ask which values of are defined. Equations that are not identities are actually questions: For what satisfy this equations. In this example we must have , and therefore Finding the solutions of a trigonometric equation usually involves recognizing identities in order to obtain a workable form of the equation. For example, can be rewritten 120.htm[6/6/2013 1:02:31 PM] 120.htm Thus must be either or , with . We then conclude is the complete solution to the original equation. As with solving any equation, factoring is an important technique. For example, the equation can be written and, since Therefore , we must have because has no real solution. is the complete solution. In practice, we often look for solutions on a restricted domain. For example, if we want the solution to this equation with then we have Most identities that we will need can be derived from the basic ones we have already verified along with the fundamental definitions. For example, suppose we want to expand We have by definition and so However, it might be useful in context to express this identity entirely in terms of the tangent function. One way to do this would be to divide to obtain numerator and denominator by As an exercise, you should use this approach to obtain identities for , , and entirely in terms of each function, respectively. You can now verify the cotrig identities, which generalize right-triangle trigonometry for the trigonometric functions: This strategy also works for the so-called half-angle identities. Consider, for example, the function (We have seen that the period of this function is 120.htm[6/6/2013 1:02:31 PM] .) Suppose we want to write this function entirely in terms of the input instead of . 120.htm We reason as follows: Since this is an identity we deduce Now we can solve for in terms of This identity, however, introduce certain difficulties. For example, if then the LHS is clearly ; but we cannot evaluate the RHS without some theorems from calculus. Also, the sign ambiguity in the numerator must be resolved by determining in which quadrants of the unit circle the angles and are located. (Which sign would you choose if ? What about ?) It is possible to write the halfangle identity for the tangent without the sign ambiguity. First, we obtain half-angle identities for sine and cosine, using Using the same reasoning as for the tangent we obtain Each of these has a sign ambiguity that must be resolved by locating the quadrants for and . But now Notice that the LHS is defined precisely when the RHS is defined, so we can now work with the fraction It follows that because . Finally, if is in the second or fourth quadrant and so which we can also write as 120.htm[6/6/2013 1:02:31 PM] then because is in the first or third quadrant. But if . Thus, in either case, we can write then 120.htm It follows that we can write our function as With just the basic identities you can also verify conversions between sums and products, such as Inverse Trigonometric Functions If a function is one-to-one on its domain ( the property that for all in the domain of . We say that for all in the domain of unless and ) then there is a function . Since each of the fundamental trigonometric functions is many-to-one on its whole domain, it is necessary to and the full range of we can find a unique This function function by has is defined by then one-to-one on the is attained on this interval, so it is a good candidate for a restricted domain. Given any real number such that as its domain and However, because , in other words, as its range. Borrowing the generic inverse function notation we often denote this this notation can be confusing, so we will generally use This notation reminds us that the trigonometric functions are defined on the unit circle: For example, is the radian measure in the interval of an arc on the unit circle whose tangent is reflecting the graph : 120.htm[6/6/2013 1:02:31 PM] with are inverse functions of each other because it is also true that restrict the domain in order to define an inverse function. For example, if the function interval whose domain is the range of in the line . The graph means that is obtained by 120.htm Notice that the vertical asymptotes for have become horizontal asymptotes after reflection in . The function is extremely useful in mathematics and its applications. Note that we can restate the superposition theorem for harmonic motion in terms of this function. Theorem. Let , with . Then . Alternatively, . Inverse functions for the other fundamental trigonometric functions can be defined similarly. The domains are usually restricted so that because of the identities Thus, 120.htm[6/6/2013 1:02:31 PM] 120.htm , with (dashed) which means that we restrict the domain of on to , since that is the range of , whose graph is reflection of . , with (dashed) The restricted domains for the other four functions are then obtained so that compositions among the trigonometric functions and their inverses agree with the properties of right-triangle trigonometry. For restricted domain is 120.htm[6/6/2013 1:02:31 PM] : the restricted domain is , and for the 120.htm , with , with Then 120.htm[6/6/2013 1:02:31 PM] (dashed) (dashed) has as its range, which is also the restricted domain for . 120.htm , with (dashed) has Finally, , with 120.htm[6/6/2013 1:02:31 PM] (dashed) as its range, which is also the restricted domain for . 120.htm Composition of Trigonometric and Inverse Trigonometric Functions By definition, the composition of with that it is consistent with the definition of , in either direction, is the identity function, provided we restrict the domain of so . This will be important when we form the compositions of the fundamental trigonometric functions with the inverse functions of the others. Here is a summary of those domains, which are the ranges of the inverse functions :: A common source of error, particularly when using calculators for applied problems, is failure to observe these domains, particularly because but the choice of restricted domain can vary in applications as well as in software design. As a simple example, ; however, for all . As we derive formulations for other compositions we will assume the domains of the trigonometric functions have been declared as in the table above. Note, however, that the choice of restricted domains can vary from text to text, and, more importantly, from one type of software to another. In particular, if you have a graphing calculator try graphing . there is a good chance it will display in the range instead of To continue, consider Thus composition. Let . and . Then because of the fundamental cotrig identity. However, we can be more explicit about this , which we have seen is in . Then and so and so The sign ambiguity can be resolved by our precise definition of the functions involved. In fact, since We can now begin to construct a composition table, where we list the function intersection of row and column records the function 120.htm[6/6/2013 1:02:31 PM] : it follows that in the left column and the function in the top row; the 120.htm Note that if is the inverse function of then . For example, if and This is the result we would expect from right-triangle trigonometry, but now we see that it is true when when, for example, is any real number. To evaluate and Here again the sign ambiguity is resolved by the fact that sine is an odd function and that the sign of two more entries in the table because Exercise. Show that the remaining entries in the table are as follows. Explain, for example, why 120.htm[6/6/2013 1:02:31 PM] we have matches the sign of . We now have is always positive. 120.htm Special Topic: What about ? Not all of these compositions are possible. For example, if composition is only defined at the isolated points where domain of range of . Which of the other is and is . Similarly, is also then the is only defined when the range of compositions are not possible? On the other hand, if and the domain of Note, however, that the range of , because is only within the and then the , so the composition is possible. To evaluate it, note that so this evaluation is only valid for in , which is precisely the restricted domain of , and, by the same reasoning, and . The other compositions are not so easily obtained. The attempt to understand them was an important development in calculus. For example, is there any way to simplify range of is 120.htm[6/6/2013 1:02:31 PM] and the graph on the interval ? Since the range of looks like is the 120.htm with tangent line for Further, with and in terms of related angles Let and . Here is such a construction using the unit circle: and suppose the terminal ray corresponding to horizontal line through intersect the tangent line to the circle at , that is, changes from to changing at a constant rate from 120.htm[6/6/2013 1:02:31 PM] , and let be the angle . Let be the point where the . Then and to . How would we describe the rate at which the angle ? It is certainly not a constant rate of change. In fact, it can be shown with basic calculus that its rate of change is given by the function on the interval intersects the unit circle at . This is a geometric definition of the function graphed above. One way to understand its properties is to imagine the angle The graph of . Mathematicians constructed geometric figures to express this equation looks like 120.htm gives the slope of the tangent line at the point on the graph and the slope of the tangent line is . For example, if then . What is the slope of the tangent line to the graph at the origin? The following eight compositions are obtained similarly, and their graphs are constructed from their rates of change as given by each in the domain. 120.htm[6/6/2013 1:02:31 PM] for 120.htm , , 120.htm[6/6/2013 1:02:31 PM] ; ; , , 120.htm 120.htm[6/6/2013 1:02:31 PM] , ; , ; , , 120.htm Eight more compositions are possible and can be obtained from those graphed above. For example, . The function that gives the rate of change of a function for all values of If is the derivative of and is the derivative of then the derivative of the function then , and the slope when is a straight line with slope then , that is, the function has a constant rate of change. The derivative has the following important property: For example, if is is called the derivative of . If the graph of is is . , so the slope of the tangent line to the graph of when . Use these properties together with the above graphs in the following assignment: Extra Credit Assignment: Due June 11 A point on the unit circle moves at a constant rate of and point ,where is the foot of the perpendicular through to the tangent line to the circle at to . Let . At time be the angle is the origin. a) Make a precise sketch that shows the relation between b) Determine radian per second, counterclockwise from when and when c) The graph below shows the rate of change Express the function 120.htm[6/6/2013 1:02:31 PM] explicitly in terms of . . Express of and . Express as a trigonometric function of . explicitly in terms of at each time . The range of and sketch the graph of this function. is negative because decreases as increases. 120.htm d) Find the rate of change of e) For what value of in radians per second when will the rate of change of be . radians per second? Second Midterm Exam: Areas of Focus Trigonometric equations: Finding all solutions Finding solutions within a specific interval Fundamental identities - be able to apply these when solving equations and when evaluating trig functions given values of other trig functions: Pythagorean Cofunction Addition 120.htm[6/6/2013 1:02:31 PM] 120.htm Half-Angle Harmonic motion: Given , rewrite as or as Determine amplitude, period, frequency, phase shift Find values of such that Inverse trigonometric functions: Domains and ranges Algebraic form of compositions Cofunction identities , where is an inverse trigonometric function and is a fundamental trigonometric function Chapter 8 Suggested Exercises (Swokowski/Cole, CSUSB edition) 8.1 (pages 532-534): 8.2 (pages 541-544): 8.3 (pages 554-557): 8.4 (pages 565--567): 8.5 (pages 572-574): 8.6 (page 579): Third Graded Assignment: Due May 30 To reinforce written communication skills the Graded Assignment solutions should be clearly presented in a "bluebook" or provided in .pdf format. Do not send electronic scan of handwritten work. The assignments are chosen to encourage understanding of a variety of applications, often within social and historical contexts, of developments within and related to the natural sciences. Late papers will not be graded. 120.htm[6/6/2013 1:02:31 PM] 120.htm Do any one of the following: page 533: page 543: page 544 page 555: page 567: page 574: page 579: page 582: Law of Sines Let be any triangle. In the Euclidean plane there is a unique circle through the vertices, called the circumcircle of the triangle. Let the interior angle at Then where where Sines. and let be the length of side is a right triangle and the angle at is also . Choosing either or be , let the diameter through this vertex intersect the circle at since it is subtended by arc , which also subtends the angle at . . Thus is the radius of the circle. Similarly, is the angle at Corollary. Let with opposite side be the area of triangle and is the angle at with opposite side . This is the proper statement of the Law of . Then Law of Cosines The Law of Cosines computes the length of a side of a triangle in terms of the other two sides and the opposite angle. Euclid realized this as a generalization of the Pythagorean Theorem and provides its proof in Book II of the Elements, Propositions 12 and 13. The sine and cosine functions were not explicitly defined by Euclid, but the fact that two propositions were used to state this law (one for the case where the opposite angle is obtuse and the other for the case where the opposite angle is acute) is a geometric interpretation of the fact that the cosine of an acute angle is positive whereas the cosine of an obtuse angle is negative (Note that the sine of any angle in a triangle is positive.) Here is Euclid's proof of Proposition 12, the obtuse angle case, using modern algebraic notation: Let be the obtuse angle and let outside the triangle. Let 120.htm[6/6/2013 1:02:31 PM] be the altitude from be the length of segment to side . Since is obtuse this altitude meets the line . By the Pythagorean Theorem we have at point , 120.htm Thus, Euclid concludes that the square on the side opposite the obtuse angle is greater than the sum of squares on the other two sides by the area of the rectangle on the side to which the altitude is drawn whose height is equal to the extension of that side to the foot of the altitude. The awkward language is typical of the more technical results from ancient mathematics. In modern language we would say that Then because and we have the Law of Cosines: Proposition 13 is proved similarly, but this time Euclid shows that the square on the side opposite an acute angle is less than the sum of squares on the other two sides by the area of a rectangle. Using the cosine notation we do not need a separate law, because now so and . This is an example of how modern mathematics simplifies cases by introducing the language of functions. Heron's Formula for the Area of a Triangle: Since we have and from the Law of Sines thus Now, using the Law of Cosines where , the semi-perimeter of the triangle. The square of the area of the triangle can now be written as a simple formula using only the lengths of the sides: 120.htm[6/6/2013 1:02:31 PM] 120.htm Corollary: Radius of the circumcircle. Vectors Representations and complex numbers A vector is a quantity that is characterized by magnitude and direction. Vectors are defined in any dimension but we will only study them here in the plane. The segment has a length determined by the distance formula, but no in two dimensions. Consider two points and direction. If we can specify a direction, for example, from represents a vector. (If . The directed line segment , sometimes called an arrow, the segment reduces to a single point and represents the zero vector, whose magnitude is undefined.) Any directed line segment parallel to , direction. For example, if or complex numbers represents the same vector, as long as the arrow points in the same and , then and and represent the same vector. We say that . We will interchangeably represent points in the plane by either ordered pairs . Thus, every vector can be represented by an arrow from , for unique values of and whose direction is with length the arrows are equivalent; in particular, both arrows have length complex number to to , equivalently by a . Unit vectors and the unit circle The magnitude of a vector is easy to compute as a non-negative number. Since the vector can be represented by corresponds to the ray with vertex The arrow has length that contains . This ray intersects the unit circle at . A vector whose magnitude is elementary texts this complex number is abbreviated by the acronym where is the natural log base ( is denoted The unit vectors corresponding to is . In many ), so we will use this notation. In the abstract, it is common to notate vectors with bold letters. and are often denoted and direction . If it follows that the direction of is the unit vector and , respectively. As complex numbers we have . It follows that the vector is represented by the complex number which is called the polar form. In the polar form of a complex number, the angle 120.htm[6/6/2013 1:02:31 PM] . . However, it is shown in calculus that , which in context may be abbreviated to In general, suppose a vector has magnitude Addition and scalar multiplication for some is called a unit vector. Thus, the direction of any non-zero vector can be described by a unit vector; equivalently, by a point on the unit circle. As a complex number, the point The magnitude of vector its direction is called its argument. 120.htm Vectors were developed historically in two related contexts: physics and geometry. These two contexts are naturally related by the need to represent translation through a distance and physical quantities that depend on translations, such as velocity and force. For example, to describe the velocity of an object it is necessary to represent both its speed (distance/time) and its direction of motion. Even before the invention of calculus it was discovered that translations, forces and velocities add according to vector rules: If and are represented by arrows and then is represented by the arrow , where is the fourth vertex of the parallelogram parallelogram law of addition. Notice that this law is equivalent to the coordinate addition law: If and For example, if then , where and . This was known as the . then , using are the complex number representation. To summarize, the other standard representations of where and The representation is sometimes called the component form of the vector. Another notation for the . This notation is used to avoid confusion between the point and the vector representation is . Thus where . Context determines . which of these equivalent notations is used. Note that There is a natural way to change the magnitude of a vector. If is a real number then The multiplication of a vector by a real number is called scalar multiplication and it is applied to any of the standard representations, above, by multiplying each component or coordinate by . Consequently, . If then is the zero vector. If then the direction of is opposite the direction of . In particular, is the vector whose unit vector is parallelogram law says that if and if the unit vector for then is . Also, since is represented by the arrow the in the parallelogram. Dot product, Angles and Law of Cosines While complex numbers can be used to represent vectors in the plane (because the real and imaginary parts are the coordinates of a point) they also behave like the real numbers that they generalize: they can be added multiplied and divided. The addition of complex numbers corresponds to their addition as vectors, and the multiplication of a complex number by a real number corresponds to scalar multiplication. However, the multiplication of two complex numbers generally does not directly correspond to a vector operation (physically, the multiplication of two forces or two velocities is not a natural phenomenon). There is another operation with two vectors that does have important applications: the scalar product, sometimes called the dot product: where is the angle between and , measured by representing the vectors as arrows not matter which angle we use. From the definition, the dot product is commutative Suppose we use the component representation and and . Since it does . Then . By the Law of Cosines, since and so 120.htm[6/6/2013 1:02:31 PM] is the length of side in the triangle , we have 120.htm Therefore, when and are written in component form, from which it is easy to see that and For example, if and are represented by the complex numbers and as above, then , and the angle between these vectors is found by Now , so Normally we state the angle , as expected. between two vectors so that . The dot product offers a lot of flexibility in describing the geometry of vectors. Note that and that (Be careful to distinguish between the vector and the scalar .) Whenever we say that the two vectors are orthogonal. If neither is the zero vector then they are orthogonal precisely when the angle between them is . If or we say the vectors are parallel; these two cases maximize and minimize the scalar product. Projection and Reflection Consider a vector written in component form . We say that is the component in the direction and is the component in the direction . Note that where non-zero vector is the unit vector for . Let 120.htm[6/6/2013 1:02:31 PM] . We can generalize this idea by defining the component of any vector relative to a given 120.htm the dot product of and the unit vector for If then is parallel to directions. Note that that is sometimes denoted Exercise. If and if if and . If this unit vector is and and the unit vector for have the same direction whereas are orthogonal. When is if then and is multiplied against the unit vector for are a pair of non-zero vectors that are orthogonal, and have opposite we obtain a vector is any vector, then A vector transformation that is important in many applications is the reflection of a vector in a given line through the origin. For example, the in the horizontal axis results in the vector . Any line through the origin has Cartesian equation reflection of for a unique . One of the two unit vectors perpendicular to this line is parallel to the line. Now let The vector because the vector is and define has the same magnitude as but its arrow is in the opposite half-plane relative to the line. Specifically, Exercise. Use the dot product to show that the angle from to the line of reflection is the same as the angle from the line to . Force, velocity Even without calculus some basic applications can be described with vectors. One of the earliest discoveries described the resultant force acting on an object as the result of multiple constant forces acting on that object. Each of these forces is represented by a vector whose magnitude measures the amount of force and whose direction specifies the direction in which the force is applied. The resultant force is just the vector sum of the individual forces. Force is defined by Newton's Second Law in terms of mass, distance, and time: If mass is in kilograms, distance in meters, and time in seconds then force is in where the symbol A force of stands for Newtons. Example: acts on a body on a planar surface in the direction body in the direction The resultant force is 120.htm[6/6/2013 1:02:31 PM] . Simultaneously, as second force of acts on the . What is the resultant force? If no other forces act on the body, in what direction will it move? . The magnitude of this force is 120.htm , which is . The direction the body will move is the direction of the resultant force, which is given by the unit vector , where . . Thus Velocity also has both magnitude and direction. The magnitude of a velocity is the speed. Velocities add as vectors, which is why aircraft need to adjust velocity for the velocity of the wind so that the sum of the two results in the intended velocity. The dot product has a natural interpretation as the work done by a force acting on a body. If a force through a given distance in a given direction then where is the vector representing the displacement. Thus, if the force straight line from the origin to the point The total distance the body moves is acts on a body so as to displace it in the above example acts on a body that is constrained to move in a the work done is and the work done by the force is Note that in this case , a negative number. This means that the force vector and the displacement vector is obtuse ( , where the symbol stands for Joules. , equivalently, the angle between in this case). Note that Complex Number Arithmetic DeMoivre's Theorem We have seen that complex numbers add and subtract like vectors. This is because they have a real part and an imaginary part: We write and . Since we can also multiply complex numbers: Any complex number other than Thus we can perform division: 120.htm[6/6/2013 1:02:31 PM] has a reciprocal: 120.htm It helps to introduce the notation where if . The number is called the complex conjugate of , the reflection of in the horizontal axis. Note that The multiplicative arithmetic of complex numbers is simplified when we use the polar representation where and . If and then This allows us to interpret multiplication of complex numbers geometrically: The product of two complex numbers is the complex number whose magnitude is the product of the two magnitudes and whose argument is the sum of the two arguments. Since , it follows that This observation provides a simple method for computing integer powers. If for any integer . Let To evaluate with then, just as for non-zero real numbers, and . Thus, for any integer we first notice that and that . We then make a conjecture: We cannot prove this conjecture by simply verifying it for larger and larger values of . Instead, we use a principle from mathematical logic called the Principle of Mathematical Induction, which states that if a conjecture has been verified for some integer such as hypothesis that it is true for arbitrary allows us to deduce that it is true for have already shown that our conjecture is trivially true for where non-zero: , and the , then the conjecture is true for all positive integers. We (and we even established it for ), so now take as our hypothesis is arbitrarily chosen but unspecified. Since our hypothesis takes the form of an equation we can multiply both sides by anything The LHS is just 120.htm[6/6/2013 1:02:31 PM] whereas the RHS expands to 120.htm Therefore, we have deduced from the hypothesis This establishes De Moivre's Theorem: , If , then for every integer , Note that De Moivre's Theorem holds for negative integers without further proof because if Powers and roots then with . We now have a convenient theorem for computing integer powers of complex numbers that also allows us to solve equations of the form where is a given complex number. Apparently the solutions just is a square root of so if . For example, the solutions of are let . Then , that is, we have We conclude that and and in the interval does solutions are is chosen so that . Certainly since then Since works (it is the smallest value of . The next largest value of would be the two solutions are square roots are number roots of , but we need to be clear what we mean by the square root of a complex number. We use De Moivre's Theorem to clarify this concept. If with are all possible . The radical notation . There is no convention for non-real 120.htm[6/6/2013 1:02:31 PM] but this is not in . For example, if then . So the two , , and the two was originally defined to be the non-negative square root of the non-negative real which of the two roots we call The procedure for finding square roots works for that solves the equation), but so as opposed to roots in general: First determine . , the unique non-negative root of the real 120.htm number of ; then divide all representations of the argument of by , until the quotient is no longer in . Example: Find the cube roots . Here we want to solve Since and the roots are We can summarize this procedure in a theorem that is actually a special case of the Fundamental Theorem of Algebra: If there are exactly solutions of the equation , Mathematical Induction The proof of De Moivre's Theorem was a typical application of the Principle of Mathematical Induction. This principle is used frequently in calculus to simplify sums that depend on an integer index, such as those that occur in the theory of integration. One such sum is probably familiar The sum on the LHS depends on the index . It has been reduced to a closed formula on the RHS which only requires substitution of the index itself to evaluate. To prove that this formula is valid for any we must first establish that it is true for at least one value of the Basis Step of the induction proof. We try to find the smallest value of for which the claim is true. Here, . This is called works because Although the Basis Step is often trivial to verify, it must be carried out in precise form. Next is the Induction Step, where we hypothesize that the formula holds for an arbitrary but unspecified value of the index, and then deduce from the hypothesis that the formula holds for the next value of the index. Thus, from we want to deduce If the conjecture takes the form of an equation, as this one does, the deduction is usually carried out by altering each side of the equation to produce an equivalent equation. Here we make the LHS of the hypothesis look like the LHS of what we want to deduce by adding must add . So we to the RHS of the hypothesis as well: If our conjecture is valid it should now be possible to rewrite the LHS of this equation so that it looks exactly like the RHS of what we want to deduce: 120.htm[6/6/2013 1:02:31 PM] 120.htm We have deduced the equation when the index is theorem. from the hypothesis, when the index is . Therefore, the closed formula is actually a Binomial Theorem Historically, one of the first applications of mathematical induction was the expansion of binomials raised to integer powers. (This is the idea behind Pascal's Triangle. Newton generalized these binomial expansions to the case when the power is any real number by using infinite series techniques.) If is a non-negative integer the expansion of can be collected into terms of the form Here we assume that any expression raised to the power is formally equal to , the idea being that no expansion would be necessary if any term were zero to start with. The content of the Binomial Theorem is the determination of the coefficients coefficients, but only by construction from the previous value of . Pascal's Triangle provides these . The Binomial Theorem provides them in closed form: The symbol denotes the number of subsets of size in a set of size , that is, the number of ways to select objects from distinct objects. With this interpretation it is reasonable that the Binomial Theorem should take this form: Expanding by the distributive law involves choosing of the terms (and thus of the terms) from the factors in order to create the term . Summation notation is used for expressions of the type that occur in the Binomial Theorem: This notation represents a sum of terms indexed by , indicating there will be one term for each value of prove the Binomial Theorem we need a way to evaluate where , for any positive integer exactly one way to choose no objects from (there is exactly one subset of size objects unchosen. The formula for Basis Step. Let 120.htm[6/6/2013 1:02:31 PM] up to and including . To explicitly. We claim that . We define based on the set selection interpretation of objects, that is, there is exactly one empty subset. It follows that ). More generally, from , since choosing ; there is , and also of the objects is equivalent to leaving of the makes this symmetry obvious. We can establish this formula by Mathematical Induction: be any non-negative integer. Then because there is exactly one empty subset of the set of objects. But 120.htm , so the formula holds for Induction Step. Assume . for an arbitrary but unspecified value of . We want to deduce from this hypothesis that We need to do something to to change it to . Remember that new member to each subset. There are collections of size , and then do the same thing to is the number of subsets of size . We can make all subsets of size objects to choose from for each subset of size . But we have counted each of these collections exactly members it was counted when we augmented the resulting collection of size we need to divide by . Thus . Pascal's Lemma. Proof. The Binomial Theorem can now be stated as follows: For any non-negative integer , 120.htm[6/6/2013 1:02:31 PM] , so there are now . So to get the exact number of subsets of size This completes the induction step, so Pascal's Triangle displays the binomial coefficients by adding one times, because if we remove each of its From our hypothesis we have the equation holds for every and show this changes it into because of the following result: 120.htm Example. Find the terms in the expansion of Let and that contains the factors . We want the terms and and and . . Since these terms are . The Binomial Theorem shows how Pascal's Triangle works. If we assume for some particular but unspecified value of right side by , then we would obtain after multiplying both sides by produces whereas multiplying the right side by produces Then, after adding like terms, we have The right side is now plus terms of the form However, as we saw by Pascal's Lemma. Since thus establishing the Binomial Theorem by mathematical induction. Chapter 10 Suggested Exercises 10.4 (pages 715-716): 10.5 (pages 723-724): 120.htm[6/6/2013 1:02:31 PM] we have . Multiplying the 120.htm Fourth Graded Assignment: Due June 6 Do any one of the following: page 715: page 724: Final Exam: Areas of Focus The exam is cumulative but some material from the first two exams will be worked in. Review in particular the following ideas from those exams: Geometric relations among central angle, radius, arc length, and area of sector; Angular speed and linear speed, in correct units. Constructing graphs of linear alterations of fundamental trigonometric functions: asymptotes) Trigonometric equations: Finding all solutions or only solutions within a specific interval Use of factoring and fundamental identities Harmonic motion: Given (domain, range, intercepts, , rewrite as or as Determine amplitude, period, frequency, phase shift (in terms of Inverse trigonometric functions, particularly compositions trigonometric function ) , where is an inverse trigonometric function and Material since the first two exams covers the following ideas: Law of Cosines Vectors Representation by arrows Component form and vector addition Unit vectors and scalar multiplication Dot product and angle between vectors Force, displacement, work Complex numbers Rectangular and Polar form Arithmetic: De Moivre's Theorem and roots 120.htm[6/6/2013 1:02:31 PM] is a fundamental 120.htm Mathematical Induction Study the suggested exercises from this section Binomial Theorem Find terms in expansion of with given characteristics Conics in Polar Form Curves in the plane that are described by Cartesian equations of degree two correspond to conic sections and so are often called conics. A polynomial in and of degree two takes the form where are constant coefficients with the conic. For example, not all zero. The pairs which is just the unit circle. The affine type of the conic is determined by following theorem: Let Examples. The curve 120.htm[6/6/2013 1:02:31 PM] that make this polynomial zero are the points on gives , the coefficients of the quadratic terms, according to the . Then the conic is has , so 120.htm Figure 1. Parabola: The curve has , so Figure 2. Hyperbola: The curve 120.htm[6/6/2013 1:02:31 PM] has , so 120.htm Figure 3. Ellipse: The three affine types correspond to the ways a cone can intersect a plane. Each type has degenerate cases associated with it: If the plane intersects the cone only at its vertex we get a single point, a degenerate ellipse; if the plane is tangent to the cone we get a single line, a degenerate parabola; if the plane passes through the vertex but is not tangent we get two lines, a degenerate hyperbola. Exercise. Find coefficients that produce degenerate conics of all three types. It is often preferable to express conics in polar form by using the representation Note that this representation is equivalent to viewing each point as the complex number often simplifies the description of the conic. For example, the unit circle which we can simply write as equation In general, since . In other words, the unit circle consists of all complex numbers such that satisfy the becomes This expression suggests a "standard form" for conics: The conic passes through the origin if and only if removes the constant term. Then . This becomes satisfies the equation, and if , so apply a rigid motion that then For example, is the ellipse in Figure 3. It is easy to show that the denominator in this expression can be zero only if hyperbola. The values of such that intersect the curve a second time. For example, consider the conic 120.htm[6/6/2013 1:02:31 PM] , that is, only when the conic is a parabola or correspond to directions of lines through the origin that do not 120.htm Figure 4. Since this is a hyperbola. The denominator is zero for . The lines through the origin for these directions are and , as shown in Figure 4. It also appears that the line , the -axis, does not intersect the curve a second time. But this line is tangent to the curve at the origin. In analytic geometry we say the tangent intersects the curve twice at the point of tangency. By the same reasoning, the parabola Figure 5. 120.htm[6/6/2013 1:02:31 PM] 120.htm is intersected by the (corresponding to -axis exactly once. Every other line through the origin intersects the curve a second time, including the line , which makes ), the tangent to the curve at the origin, as shown in Figure 5. is not degenerate then the tangent line at the origin is Theorem. If the conic where . For example, the tangent line at the origin to the ellipse in Figure 3 is the ? Here -axis because yields . What about the conic . What is the Cartesian equation of the tangent at the origin, shown in Figure 6? Figure 6. The ellipse If the conic is degenerate the it is possible for the numerator and denominator of is undefined for degenerate conic is because Note, however, that cancelling the common factor 120.htm[6/6/2013 1:02:31 PM] to be zero for the same value of . For example, . The Cartesian form of this in the polar form results in , which eliminates the line 120.htm and obscures the fact that this conic is a degenerate hyperbola. Figure 7. Degenerate hyperbola Special Topic: Polar Conics and Inverse Trigonometric Functions Polar representation of curves is best understood in terms of vectors. A given input is , equivalently, the complex number the point on the curve. As direction; if produces a value , and the resulting point on the curve . Now consider the vector represented by the arrow with tail at the origin and tip at changes we can picture the length of this arrow changing. The length is the arrow points in the calculus we compute the derivative of direction; if as a function of the arrow represents the zero vector. How is in order to find the this rate of change, assuming that we introduced this idea when we studied the inverse trigonometric functions. For example, if we noted that the derivative is The polar curve 120.htm[6/6/2013 1:02:31 PM] , so if is an ellipse. Its Cartesian form is the arrow points in the changing as changes? In changes at a constant rate. Recall with , 120.htm Figure 8. The vertical axis is the tangent to this curve at the origin. We can generalize this idea to produce a standard polar form for any non-degenerate conic: We want the curve to pass through the origin and have its tangent at the origin be the vertical axis. These conditions imply that ; in particular, there is no term in the denominator. Suppose, now, that the conic is a non-degenerate ellipse, so we can represent it as with and . Then after setting and (since ). Note that this ellipse is similar to the ellipse because multiplication by is a dilation about the origin. We say that the two ellipses have the same eccentricity, which we define to be In Figure 8 we have , so and they have the same eccentricity, so we can assume eccentricity is a circle. Writing . Then the ellipse becomes and its eccentricity is 120.htm[6/6/2013 1:02:31 PM] . Thus the eccentricity of this ellipse is . Two ellipses are similar if and only if to represent all possible eccentricities. Then , let where and an ellipse with since we are assuming 120.htm Using calculus we can show that Thus, setting is the derivative of we obtain the ellipse with eccentricity Question: For the ellipse in standard form, horizontal axis? as the rate of change of this inverse trigonometric function. locates the point furthest from the vertical axis. Which points are furthest from the By symmetry, these are the two points whose -coordinate is . Since we want to solve equivalently Since the two points are , and so the maximum vertical width of the ellipse is . (The intersection of the line through these two points with the horizontal axis is called the center of the ellipse.)Note that, for , where Exercise. Let be its distance to , is the eccentricity. and . For any point on the hyperbola let be its distance to and let . Use the Law of Cosines to show Then show that . Thus: There are two points (foci) inside any ellipse, the sum of whose distances to any point on the ellipse is constant. If the ellipse is a circle then the two foci coincide (at the center of the circle). The origin and the point are called the vertices of the ellipse. This verifies the general principle that the eccentricity is the distance between the foci divided by the distance between the vertices. Hyperbolas can also be described in terms of inverse trigonometric functions. Using it is possible to express 120.htm[6/6/2013 1:02:31 PM] as the logarithmic function 120.htm from which it follows, by substituting Thus, , that is actually a real-valued function of which describes a hyperbola provided Figure 9. Setting for and the same methods from calculus show that its derivative is . For example, if with asymptotes for we can write and the eccentricity of the hyperbola is The vertices of the hyperbola are the intersections with the horizontal axis so, as with the ellipse, the distance between the vertices is . We can determine foci for the hyperbola by finding two points on the horizontal axis symmetric about the vertical line in Figure 9 that is half way between the vertices. The intersection of this vertical line and the horizontal axis is called the center of the hyperbola. Again, the eccentricity is the distance between the foci divided by the distance between the vertices: 120.htm[6/6/2013 1:02:31 PM] 120.htm so the foci are the points Exercise. Let and let and be its distance to . For any point on the hyperbola let be its distance to . Show that Thus: There are two foci for any hyperbola, the absolute difference of whose distances to any point on the hyperbola is constant. and are functions of The distances hyperbola with directions given by that have in their denominators. The two lines through the center of the are called the asymptotes of the hyperbola. These are shown in Figure 9 for the hyperbola with . Parabolas The horizontal line Consider the triangle hypotenuse , and so in polar form is with right angle at . The rate of change of , on the horizontal line, and measures how fast the hypotenuse is changing assuming parabola, with the horizontal axis as a line of symmetry. A larger value of 120.htm[6/6/2013 1:02:31 PM] as a function of is given by . Then measures the changes at a constant rate. As a polar curve results in a "wider" parabola, as in Figure 10. is a 120.htm Figure 10. and However, all of these parabolas are similar as figures in the plane since every parabola to have the same eccentricity, single focus, on the line of symmetry. Let distance between and and, since is just a dilation constant relative to the origin. Thus we expect , which agrees with the formula be the point and let since be any point on the parabola. By the Law of Cosines, if is the then , However, the distance between and the vertical axis is and Thus the distance between and is always equal to the distance between and the vertical line parabola and this vertical line its directrix. For any parabola there is a focus and a directrix with this property. 120.htm[6/6/2013 1:02:31 PM] . A parabola has a . We call the focus of the 120.htm Figure 11. Distance to focus equals distance to directrix Exercise. Let triangle be the vertex of a parabola and let be its focus. Let be a point on the parabola such that is equilateral. Project: Conics Suggested project items: Page 768: Page 780: Page 781: Page 792: Page 827: Page 827: (refer to on page 768) Due date: June 6 Format: Any standard word or math processing system may be used, but the following format must be observed. Title Page: Page 1 should contain only the following information: 120.htm[6/6/2013 1:02:31 PM] . Show that 120.htm Introduction: Starting on Page 2, explain in your own words (using complete sentences) the context of the problem you will solve. Define any terms you use and explain how the mathematics of conics is involved. Keep this introduction to a single page. Solution: Starting on Page 3, present your solution. Be clear and complete, and use your notation consistently. Separate out equations from the text. For example, most word processing software allows you to equations. If you cite references other than the course textbook then list them at the end of your solution. For example: Hermann Bondi, Relativity and Common Sense, Dover, 1986. 120.htm[6/6/2013 1:02:31 PM]