Download KIRCHHOF`S LAW KIRCHOOF`S CURRENT LAW

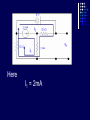
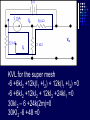
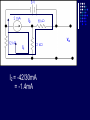
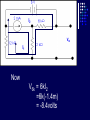
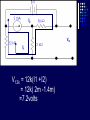
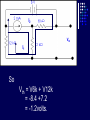
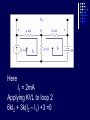
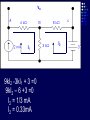
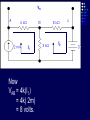
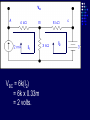
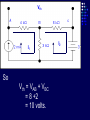
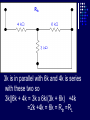
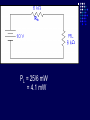
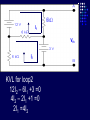
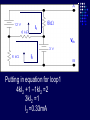
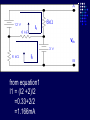
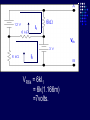
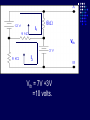
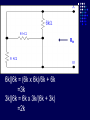
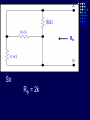
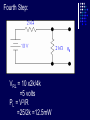
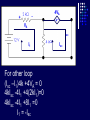
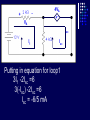
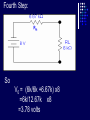
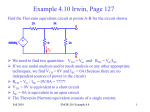
Example
We want to calculate the voltage Vo .We
will the same four steps.
First Step:
We have removed RL to calculate Vth .
Second Step:
Vth
We want to calculate Vth . Apply KVL in two
loops to calculate the individual loop
currents.
Here
I1 = 2mA
I2
Vth
I1
KVL for the super mesh
-6 +6kI2 +12k(I1 +I2) + 12k(I1 +I2) =0
-6 +6kI2 +12kI2 + 12kI2 +24kI1 =0
30kI2 – 6 +24k(2m)=0
30KI2 -6 +48 =0
I2
Vth
I1
I2 = -42/30mA
= -1.4mA
I2
Vth
I1
Now
V6k = 6kI2
=6k(-1.4m)
= -8.4volts
I2
Vth
I1
V12k = 12k(I1 +I2)
= 12k( 2m -1.4m)
=7.2volts
I2
Vth
I1
So
Vth = V6k + V12k
= -8.4 +7.2
= -1.2volts.
Third Step:
6k is in series with 12k .The resultant of
these two is in parallel with 12k.
(6k+12k)||12k = 18k x12k/(12k+18k)
=7.2k
Fourth Step:
V0 = -1.2 x4k/(7.2k + 4k)
= - 0 .4285 volts.
Example
We want to calculate the value of RL and
the maximum power dissipation across it
by Thevenin’s Theorem.
First Step:
To remove RL to calculate Vth .In this case
our Rth is our RL.
Second Step:
Vth
A
c
We want to calculate Vth . Apply KVL in two
loops to calculate the individual loop
currents.
Here
I1 = 2mA
Applying KVL to loop 2
6kI2 + 3k(I2 – I1) +3 =0
Vth
c
A
I1
9kI2 -3kI1 + 3 =0
9kI2 – 6 +3 =0
I2 = 1/3 mA
I2 = 0.33mA
I2
Vth
c
A
I1
Now
VAB = 4k(I1)
= 4k( 2m)
= 8 volts.
I2
Vth
c
A
I1
VBC = 6k(I2)
= 6k x 0.33m
= 2 volts.
I2
Vth
c
A
I1
So
Vth = VAB + VBC
= 8 +2
= 10 volts.
I2
Third Step:
To calculate Rth .Short circuiting the voltage
source and open circuiting the current
source.
V
Rth
Rth
th
c
A
I1
I2
3k is in parallel with 6k and 4k is series
with these two so
3k||6k + 4k = 3k x 6k/(3k + 6k) +4k
=2k +4k = 6k = Rth =RL
Fourth Step:
For maximum power dissipation
RL =Rth = 6k
PL = I2R
=(10/12k)2 (6k)
Rth
PL = 25/6 mW
= 4.1 mW
Example
We want to calculate the value of RL and
the maximum power dissipation across it
by Thevenin’s Theorem.
First Step:
To remove RL to calculate Vth .In this case
our Rth is our RL.
Second Step:
KVL for loop1
-12 +12I1 – 6I2 = 0
2I1 – I2 =2
6k
I1
Vth
I2
KVL for loop2
12I2 – 6I1 +3 =0
4I2 – 2I1 +1 =0
2I1 =4I2
I1
6k
Vth
I2
Putting in equation for loop1
4kI2 +1 –1kI2 =2
3kI2 =1
I2 =0.33mA
I1
6k
Vth
I2
from equation1
I1 = (I2 +2)/2
=0.33+2/2
=1.166mA
I1
6k
Vth
I2
VR6k = 6kI1
= 6k(1.166m)
=7volts.
I1
6k
Vth
I2
Vth = 7V +3V
=10 volts.
Third Step:
We want to calculate Rth
6k is in parallel with 6k .The resultant is
again parallel with third 6k resistor.
6k
Rth
6k||6k = (6k x 6k)/6k + 6k
=3k
3k||6k = 6k x 3k/(6k + 3k)
=2k
6k
Rth
So
Rth = 2k
Fourth Step:
VRL = 10 x2k/4k
=5 volts
PL = V2/R
=25/2k =12.5mW
THEVENIN’S THEOREM and
DEPENDENT SOURCES.
Working with dependent sources is
different from working with
independent sources while applying
Thevenin’s theorem .
 While calculating Rth we can simply
open circuit current sources and short
circuit voltage sources.

THEVENIN’S THEOREM and
DEPENDENT SOURCES.

Because the voltage or current of the
dependent sources is dependent on
the voltage or current of these
independent spources.
THEVENIN’S THEOREM and
DEPENDENT SOURCES.

While calculating Rth we will short
circuit the open terminals of the
Thevenin circuit and will calculate the
Isc and then divide Vth with Isc to
calculate Rth.
Example
We want to calculate the voltage Vo by
Thevenin’s theorem.
First Step:
To remove RL to calculate Vth .
Second Step:
++
VV
A
A
--
++- 4V
A
4V
A
VV
0
th
Voltage across 4k resistor
V4k = (4k/6k) 12
=8volts
Voltage across 2k resistor
V2k= (2k/6k) 12 = 4volts.
++
VV
A
A
--
++- 4V
A
4V
A
Vth = 8 – 4VA
= 8 – 4(4)
= 8 – 16
= -8 volts.
VV
0
th
Third Step:
We will first find Isc to calculate Rth.
Here
VA = 2kI1
-
+
4VA
+-
VA
Isc
I1
Applying KVL to loop 1
-12 +2kI1 +(I1 – Isc)4k=0
-12 +2kI1 +4kI1 – 4kIsc=0
6kI1 -4kIsc =12
Isc
-
+
4VA
+-
VA
Isc
I1
For other loop
(Isc –I1)4k +4VA = 0
4kIsc -4I1 +4(2kI1)=0
4kIsc -4I1 +8I1 =0
I1 = -Isc
Isc
-
+
4VA
+-
VA
Isc
I1
Isc
Putting in equation for loop1
3I1 -2Isc =6
3(-Isc) -2Isc =6
Isc = -6/5 mA
-
+
4VA
+-
VA
Isc
I1
So
Rth = Vth/Isc
= -8/(-6/5 m)
=6.67k
Isc
Fourth Step:
So
V0 = (6k/6k +6.67k) x8
=6k/12.67k x8
=3.78 volts