Download Induced Electromotive Force (Faraday`s Law)

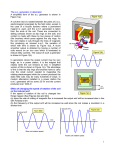
Physics 102
Lab Brief
Induced Electromotive Force
Faraday’s Law
March 11, 2010
Ch-ch-ch-ch-changes
This week’s installment is a survey of Faraday’s Law. Because Faraday’s Law involves dynamic
fields and responses, we use a system with two coils. The primary coil produces a magnetic field
which we are free to change while the secondary coil responds to these changes.
So what is Faraday’s Law? In words, nature is not cool with changes in magnetic flux. In fact,
it opposes changes in magnetic flux by inducing a potential that would produce a current that
generates a magnetic field counteracting the initial change in flux. Mathematically,
ε=−
dΦ
,
dt
(1)
where the electromotive force1 (or EMF), ε, is a system’s response to a temporally varying flux, Φ.
What’s flux? In this case, the flux is of the magnetic field, and it’s how much of the field passes
through2 some surface:
Φ = B · A = BA cos θB,A
(2)
The area vector A has a magnitude equal to the area of the surface and its direction is defined by
a vector perpendicular to the surface, and θB,A is the angle between the vectors. So what’s this
surface anyway? It depends on the system, but it’s the region of space through which the changing
flux permeates. In our case, this region is defined by the plane of the secondary (or search) coil.
How can Φ change? Looking at Equation (2), we see that we have three choices: A, B, and
cos θB,A . If A or B depend on time, then so does the flux. Even with a constant A and B, however,
we get a time-dependent flux if θB,A changes with time (as in electric generators, for instance).
Because it’s hard to train a large conducting amoeba to assume the shape we want at any given
time, this lab only considers time varying fields. The angle θB,A is also varied, but not as an explicit
function of time.
Here’s how we plan to observe induction. We need a source of B(t) and something to gauge
the response. This is precisely what the primary and secondary coils are, respectively. Given some
time varying current I(t), the functional form of the field produced by the primary coil is
B(t) =
µ0 N I(t)
,
D
(3)
where D is the diameter of the coil and N is the number of turns. Our secondary coil has a diameter
d defining an area πd2 /4. Using Equation (2), the flux of the primary’s field through the n turn
secondary is
Φ = nBprim · Asec = nB(t)A cos θB,A = n
µ0 N I(t) πd2
cos θB,A = k cos θB,A I(t),
D
4
(4)
where k just absorbs all the constants. Now we can get at the EMF. It results from Faraday’s Law:
ε=−
dΦ
dI(t)
= −k cos θB,A
.
dt
dt
(5)
1
This is a misnomer, as it’s not really a force. In fact, it has units of electric potential.
To use an example we can all relate to, consider a butterfly net. Furthermore, assume a friend has a butterfly
cannon that shoots a constant stream of butterflies. How do you collect the most butterflies? You maximize the flux
by holding the net face-on (from the cannon’s perspective) in the stream. If you hold it edge on, you’re just going to
end up with a mess.
2
1
The experiment boils down to this last equation. Our task is to plot the EMF as a function of
dI(t)/dt. We end up evaluating the derivative at some time t0 , therefore plot
dI(t) ε = −k cos θB,A
.
(6)
dt t=t0
To go any further, we have to know the details of I(t) and coil orientations. We use two different
functional forms for I(t): a triangular wave and a sinusoidal wave. In view of Equation (6),
what distinguishes the two is the derivative term. As for orientations, we’ll initially have the coils
coplanar, then vary the angle between them. Let’s examine these cases individually.
For the triangular wave, the current ramps up at a constant rate until it reaches a maximum
value. It then descends in the same manner until reaching a minimum value. Therefore, the
derivative is a square wave: it attains a positive value when the current is increasing and a negative
value when it decreases. We work with individual rising and falling intervals of the cycle to avoid
complications. The size of the intervals, how long it takes to reach it’s extremum values, depends
on the frequency of the input signal set on the waveform generator. Because the derivative is
constant,3 we get that dI(t)/dt → ∆I/∆t and don’t have to evaluate it at a particular time. Keep
in mind, however, when the current is rising and falling. Substituting this into Equation (6), we
get that
∆I
ε = −k cos θB,A
,
(7)
∆t
where the sign of ε depends on the sign of the derivative, and that depends on whether the current
is rising or falling. The important part, however, is that if we change how fast the current changes
(that is, if we change the frequency of the input current waveform) we get a different EMF, and it
is this very dependence that we aim to plot. The final simplification is setting θB,A = 0, since the
coils are coplanar in this case. This leaves us with
ε = −k
∆I
.
∆t
(8)
The relationship is linear in the current derivative and predicts a slope k, which we know a priori.
We get a more interesting term when the current varies sinusoidally. Supposing a frequency f
and amplitude I0 , we have that I(t) = I0 sin(2πf t). The derivative is
dI(t)
= 2πf I0 cos(2πf t).
dt
(9)
This, and consequently the EMF, has its maximum value at t = 0. For simplicity, we’ll just say
t0 = 0, and so ε = ε0 , in Equation (6):
ε0 = −k cos θB,A [2πf I0 cos(2πf · 0)] = −2πkf I0 cos θB,A
(10)
Again, the coils are coplanar:
ε0 = −2πkI0 f .
(11)
This is another linear relation with a slope related to a slew of things that we measure, set, or
otherwise know.
3
Technically, that’s a lie since it changes sign. But that’s all it does. It is indeed constant within rising or falling
intervals.
2
CH2
primary
secondary
coil
coil
R
CH1
Figure 1: Depicted here is the circuit for the induction lab. The coils are represented as inductors. The oscilloscope
channels are shown separately for convenience (they are indeed both on the same apparatus). Channel 1 measures
the voltage across the resistor while channel two measures the induced EMF across the secondary coil. The scope
shares a common ground with the circuit (not shown explicitly).
The last variation we investigate is spatial. We want to study the EMF as a function of cos θB,A .
As such, we leave the frequency at some nominal value f0 . We expect the EMF to be
ε = −2πkf0 I0 cos(2πf0 t) cos θB,A .
(12)
This and the EMF, again, are maximum at t = 0:
ε0 = −2πkf0 I0 cos θB,A .
(13)
Now’s the time where linearization should come to mind.
Phew, that was a lot of background. With all that under our belts, we’ll segue into comments
about the measurement procedure.
Our Friend, the Oscilloscope
The setup (Figure 1) is fairly straight forward. We have two coils. The primary coil is connected to
a resistor and function generator. The function generator is the device that produces the waveforms
we need. The resistor (connected to the primary coil) and the secondary coil are hooked up to the
oscilloscope. Remember that oscilloscopes only yield two types of information: voltages and times.4
We’ll see two signals (Figure 2) on the scope: the signal across the resistor (top red input curves in
figure), from which we deduce the one in the primary coil, and the one induced on the secondary
coil (bottom blue output curves). How are they related? A glance at Equation (6) suggests that the
secondary coil signal is the derivative of the primary coil signal. The quantitative measurements
(also depicted in the figure) come in three flavors which we’ll taste separately.
Equation (8) requires that we determine ∆V /∆t for the input signal.5 Since the scope shows
the voltage as a function of time, we just read a pair of voltages and times off the screen to calculate
∆V and ∆t as in the top curve in Figure 2(a) (mind the scales). Use larger intervals for better
results, but avoid the rounded peaks of the signal. Now compare the slope with the amplitude
(peak-to-peak/2) for the signal in the secondary coil (labeled ε in the bottom curve of the figure).
Recall that in Equation (11), we set t0 = 0. What ramification does that have on our measurements? At that time, the induced EMF is maximum, so we just measure the maximum EMF
(ε0 in Figure 2(b)). In addition, for the right hand side of that equation, we need the frequency.
Measure this. Do not trust what the function generator claims.
4
Looking back at the boxed equations in the last section, you’ll notice that one of the measurements requires that
we get ∆I. Do any useful laws involving currents and, I don’t know, resistors come to mind?
5
See the footnote right above this one.
3
V1
V1
T →f
∆V
t1
t1
∆t
V2
V2
ε0
ε
t2
(a) Triangular waveform input
t2
(b) Sinusoidal waveform input
Figure 2: The signals portrayed above correspond to what you might observe on the oscilloscope with an ideal
system. The first part of the experiment concerns (a) while the next two deal with (b). The relevant measurements
for each are noted on the plots. Note further that the inputs and outputs have different axes labels, emphasizing that
there is a difference in scales between the plots. Typically inputs are in the V range while the EMF registers in the
mV ballpark. Furthermore, the amplitude of the input and output signals is different for both waveform inputs.
Equation (13) introduces the angle variations. Aside from measuring angles, we end up making
the same measurement for the other part using a sinusoidal input. Namely, we read the maximum
EMF off the scope. What is different is that we do not vary the frequency of the input signal for
this part. Set some initial value, measure it, and leave it be. The only other thing of concern is the
linearization, which I’m sure you’re all experts at now.
So what’s the point of all these plots anyway? Remember we’re trying to assess Faraday’s Law.
All three equations were derived from it and predict values for k. Notice that it appears in all
the relations. Furthermore, we know k independently of the plots (since it’s just given by some
constants and the geometry of the system). Bam! We have a way to quantitatively assess the
predictions of Faraday’s Law. Percent errors ahoy!
Uncertainties
Thankfully, the uncertainty propagation for this lab is nowhere near as obscene as the recent ones
we’ve dealt with. Unfortunately, it is still quite tedious to calculate. We have three relations to
plot (the boxed equations from two sections ago) and need the error bars for both axes of each
plot. Let’s tackle these one at a time.
Three quantities have an associated uncertainty in Equation (8): ε, ∆I, and ∆t. But we don’t
actually measure ∆I, we get ∆V , but let’s postpone discussing that for a while. Another subtlety
is that we don’t actually measure ∆V and ∆t, we calculate them from two pairs of points: V1 , V2
and t1 , t2 . Each of these pairs has an uncertainty determined by how well you can read off the
values from the scope. Assuming these are δV1 , δV2 , δt1 and δt2 , the uncertainties in ∆V and ∆t
are
q
q
2
2
δ(∆V ) = δV1 + δV2 and δ(∆t) = δt21 + δt22
(14)
We can simplify this by assuming that δV1 = δV2 = δV and δt1 = δt2 = δt:
√
√
δ(∆V ) = 2δV ; δ(∆t) = 2δt.
(15)
4
Since we’re dividing ∆V and ∆t, we have to add their fractional uncertainties in quadrature:
s
s
2
∆V
δ(∆V ) 2
δ(∆t) 2 √
δV 2
δt
∆V
+
= 2
+
.
(16)
δ
=
∆t
∆t
∆V
∆t
∆V
∆t
So what about ∆I/∆t? That’s what we’re after right? Remember Ohm’s Law? Of course you do:
∆I
1 ∆V
=
.
∆t
R ∆t
(17)
Recall that when multiplying quantities with uncertainties, the fractional uncertainty in the product is the quadrature sum of the fractional uncertainties of the factors. That gives us our final
expression,
v
"
u 2
2 #
δR
∆I
1 ∆V u
δV 2
δt
t
δ
=
+2
+
,
(18)
∆t
R ∆t
R
∆V
∆t
which is just aching to be evaluated in Excel.
The uncertainty in ε is estimated just as δV .6 The same quantity appears in the other plots,
so this applies to all.
A subtlety similar to the aforementioned one applies for Equation (11). The frequency is not
directly measured. Rather, it is calculated from the period. The period, in turn, is calculated from
two times. Thus, the uncertainty in the period is similar to the uncertainty δ(∆t) from above. The
fractional uncertainty is
√
√
δT
δt
δT = 2δt ⇒
= 2
,
(19)
T
T
where δt is defined in the same way as before. The fractional uncertainties of the period and
frequency are the same, yielding
√
δf
δt
= 2
.
(20)
f
T
The other thing we calculate is I0 via the measurement of V0 . The fractional uncertainty in I0 is
s δI0
δR 2
δV 2
=
+
(21)
I0
R
V0
Adding these last two in quadrature results in the fractional uncertainty of their product:
s s
2 2 √
V0
δf 2
δI0 2 V0
δt
δR
δV 2
δ(I0 f ) =
f
+
=
f
2
+
+
R
f
I0
R
T
R
V0
s 2 V0
δt 2
δR
δV 2
⇒ δ(I0 f ) =
f 2
+
+
R
T
R
V0
(22)
(23)
Onto the last plot.
6
What I mean is that it’s just the uncertainty from reading it off the scope. However, it’s not the same size as
δV . Why? I warned you about minding your scales.
5
From Equation (13), notice that we need δI0 /I0 , δf0 /f0 , and δ(cos θ)/ cos θ (I’ve dropped the
subscript for convenience). The first two we already know from the previous calculation:
s δt
δf0 √
δI0
δR 2
δV 2
= 2
;
=
+
.
(24)
f0
T0
I0
R
V0
The last man standing is δ(cos θ). What are we measuring? We measure the angle θ with some
uncertainty δθ. This time we need derivatives:
δ(cos θ)
1 d(cos θ) 1
sin θ
=
δθ =
|− sin θδθ| =
δθ = tan θδθ
(25)
cos θ
cos θ
dθ
cos θ
cos θ
Once again, we add in quadrature:
V0
δ(f0 I0 cos θ) = f0 cos θ
R
s 2 δt 2
δR
δV 2
2
+
+
+ (tan θδθ)2
T0
R
V0
(26)
Alright, so what do we have so far? Each of the boxed equations in this section yield the
uncertainty of the data points for one axes of your plot.7 Once you have error bars you can find
the uncertainty in the slope of your fit, which, if things are set up right, is the uncertainty in your
experimentally determined value of k. We compare this with our a priori value for k. But how well
do we know k anyway? Let’s remind ourselves of how k is defined:
k≡
µ0 nN πd2
.
4D
(27)
Uh oh. That definition has quantities with uncertainty, which means our expected k has some
uncertainty. Once more then, from the top. Assume we measure D ± δD and d ± δd. We need the
uncertainty in the fraction d2 /D. This results from a quadrature sum:
s
2
2
d
δD 2
d
δ(d2 ) 2
=
+
.
(28)
δ
D
D
d2
D
Only the first term under the radical needs calculation:
δ(d2 ) = 2dδd ⇒
δ(d2 )
δd
=2 .
2
d
d
With that, we have the uncertainty in the expected value of k:
s
s
µ0 nN πd2
δ(d2 ) 2
δD 2 µ0 nN πd2
δd 2
δD 2
δk =
+
=
2
+
4D
d2
D
4D
d
D
s µ0 nN πd2
δd 2
δD 2
δk =
4
+
4D
d
D
(29)
(30)
(31)
Alright, we have four k’s; three determined from plots and one calculated from the system parameters. Compare the experimentally determined ones to the expected calculated one. If the
7
Recall that the uncertainty for the ε-axis was simply the read-off uncertainty, like δV .
6
uncertainties overlap, you are in agreement with theory. The error suggests how closely you agree
with theory, and the uncertainty hints at how seriously you can take that assessment. Large uncertainties mitigate agreement with expectations since they inherently accommodate more values.
Small uncertainties yield more definitive results because they are more discriminating, but may
exclude expected values for the same reason. Hence, it’s important to correctly estimate your
uncertainties.
Hmm. Now that wasn’t very brief, was it? But I’d be remiss if we didn’t take a little time to
talk about Michael.
This Is It
Michael Faraday8 is probably the Chuck Norris of experimentalists. With little formal education
(he didn’t know much calculus or higher math and apparently never wrote an equation down in his
notebooks), discovered some fundamental principles in electromagnetism and electrochemistry. He
invented a precursor to the Bunsen burner, discovered what are now called nanoparticles, coined
many terms such as ion, cathode, anode, and electrode. The Faraday cage and the Farad are
named in his honor. It wasn’t easy either, as he wasn’t considered a “gentleman” in English
society, consequently putting up with a lot of BS. For instance, he had to serve as his advisor’s
valet, in addition to his lab assistant duties, and his advisor’s wife refused to treat him as a social
equal. Faraday almost gave up on science altogether as a result. Now, however, he’s considered the
greatest experimentalist of all time. Moreover, you know you’re a bamf if Einstein kept a picture of
you around in his study.9 He was also a bit sassy. When asked about the practical use of electricity
by the British Minister of Finance, William Gladstone, he quipped: “One day sir, you may tax it.”
Figure 3: Induced current. Hover text reads: The MythBusters need to tackle whether a black hole from the LHC
could really destroy the world. Courtesy xkcd comics.
8
Contrary to popular belief, he was not named after the law of induction, even though induction had been around
long before him.
9
Einstein also had a man-crush on Isaac Newton and James Clerk Maxwell.
7