Download 7.6 Modeling Data: Exponential, Logarithmic, and Quadratic Functions

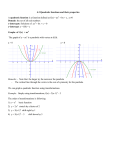
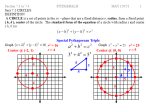
7.6
Modeling Data: Exponential,
Logarithmic, and Quadratic
Functions
Modeling Data: Relationship between
Literacy and Mortality Rate
• Scatter Plot—data presented as a set of points
• Regression Line—the line that best fits those
points
Each point
represents a
country
Scatter Plots & Regression Lines
• Scatter Plot—data presented as a set of points
• Regression Line—the line that best fits those
points
y = -2.3x + 255
f(x) = -2.3x + 255
Modeling with Exponential Function
• Exponential Function—
y = bx
or f(x) = bx
where b is a positive constant other than 1 and b > 0
and and x is a real number.
• E.g.
f(x) = 3x
g(x) = 5 x
Graphing an exponential function
• Graph: f(x) = 2x
x
f(x) = 2x
(x, y)
-3
-2
f(-2) = 2-3 = 1/8
f(-2) = 2-2 = ¼
(-3, 1/8)
(-2, ¼)
-1
0
1
f(-1) = 2-1 = ½
f(0) = 20 = 1
f(1) = 21 = 2
(-1. ½)
(0, 1)
(1, 2)
2
3
f(2) = 22 = 4
f(3) = 23 = 8
(2, 4)
(3, 8)
Graphing a exponential function
• Graph: f(x) = 2x
x
-3
(x, y)
(-3, 1/8)
-2
-1
0
(-2, ¼)
(-1. ½)
(0, 1)
1
2
3
(1, 2)
(2, 4)
(3, 8)
Other Exponential Functions
• f(x) = 2x + 5
• f(x) = 3x
Comparing Linear and Exponential Models
The graphs show the world populations for seven
selected years from 1950 through 2008. One is a
bar graph and the other is scatter plot.
Comparing Linear and Exponential Models
Inputting the data into a
program, the following models
are produced.
• Linear model: y = ax + b
• Exponential model: y = abx
Comparing Linear and Exponential Models
1. Express each model in function notation, with
numbers rounded to 3 decimal places.


Linear model:
f(x) = 0.074x + 2.287
Exponential model:
g(x) = 2.566(1.017)x
Comparing Linear and Exponential Models
2. How well do the functions model the world
population in 2008?


Linear model:
f(x) = 0.074x + 2.287
f(59) = 0.074(59) + 2.287
f(59) ≈ 6.7
Exponential model:
g(x) = 2.566(1.017)x
g(59) = 2..566(1.017)59
g(59) ≈ 6.9
Comparing Linear and Exponential Models
3. By one projection, world population is expected to
reach 8 billion in the year 2026. Which function
serves as a better model for this prediction?
• x = 77 (2026 – 1949)
f(x) = 0.074x + 2.287
f(77) =0.074(77) + 2.287
≈8.0
g(x) = 2.566(1.017)x
g(77) = 2.566(1.017)77
≈ 9.4
It seems that linear functions serves as a better
model for the projected population 8 billion in 2026.
Logarithm of a number to some base
• We know that: 23 = 8.
• If you were asked:
Given 2y = 8, what is y? y = 3, of course.
• If you were asked:
Given 2y = 32, what is y?
• To solve for y,
log232 = y (Read: log 32 to base 2 equals y)
x=y
• 2y = 32 and log232 = y are equivalent statements.
• Log of a number to some base is the exponent of
that number to that base.
Log of a number to base 10
•
•
•
•
Given: 102 = 100,
log10100 = 2
Given: 104 = 10,000, log1010,000 = 4
Given: 102.3 = x,
log10x = 2.3
Given: 10y = x,
log10x = y
Logarithmic Functions
• Definition
Given: by = x, then y = logb x are equivalent
statements.
f(x) = logb x is the logarithmic function with
base b.
• E.g.
10y = x is equivalent to y = log10 x.
Note: log of a number is the exponent to base b.
Graphing Logarithmic Function
Graph: y = log2x.
Because y = log2x means 2y = x, we can use the
exponential form of the equation.
x = 2y
y
(x,y)
2-2 = ¼
−2
(¼,−2)
2-1 = ½
−1
(½,−1)
20 = 1
0
(1,0)
21 = 2
1
(2,1)
22 = 4
2
(4,2)
23 = 8
3
(8,3)
Temperature in Enclosed Vehicle
• When the outside air temperature is anywhere from 72°
to 96°F, the temperature in an enclosed vehicle climbs
by 43°in the first hour. The bar graph and scatter plot
are given below
Temperature (cont.)
After entering data in a
computer program, it displays
a logarithmic model y = a + b (ln x),
where ln x is called the natural
logarithm.
a. Express the model in function notation, with numbers
rounded to one decimal place.
• f(x) = -11.6 + 13.4 ln x
b. Use the function to find temperature increase, to the
nearest degree, after 50 minutes.
• f(x) = −11.6 + 13.4 ln x
f(50) = −11.6 + 13.4 ln 50
f(50) ≈ 41
Review
• Modeling with Linear Function
▫ Form:
f(x) = mx + b
▫ Example: World population as a function of year
f(x) = 0.074x + 2.287
x (number
of years
after 1949)
World
population
y = f(x)
(x, y)
11 (1960)
3.0
(11, 3.0)
21 (1970)
3.7
(21, 3.7)
31 (1980)
4.5
(31, 4.5)
41 (1990)
5.3
(41, 5.3)
51 (2000)
6.1
(51, 6.1)
Review
• Modeling with Exponential Function
▫ Form:
f(x) = abx
▫ Example: Growth of bacteria against time
f(x) = 100 · 2x
Modeling with Quadratic Functions
• Quadratic function:
y = ax2 + bx + c or f(x) = ax2 + bx + c
• Graph of a quadratic function is a parabola
• Vertex of a parabola: the lowest (or the highest)
point in the graph.
Vertex of Parabola
• Vertex of parabola of y = ax2 + bx + c
occurs when
−𝑏
x=
(This can be proved by calculus.)
2𝑎
• E.g, y = -x2 – 2x + 3;
a = -1; b = -2; c = 3
x=
−𝑏
2𝑎
=
−(−2)
2(−1)
=
2
−2
= -1
Thus, y = -(-1)2 - 2(-1) + 3 = 4
vertex at: (-1, 4)
Graphing Quadratic Functions
Graphing Parabola
• Graph: y = x2 – 2x – 3
• Soluion:
1. Determine how the parabola opens.
a = 1; b = -2; c = -3
Since a > 0, the parabola opens upward.
2. Find the vertex.
−𝑏
−(−2)
2
x= =
= =1
2𝑎
2(1)
2
y = (1)2 – 2(1) – 3 = -5
vertex: (-1, -5)
Graphing Parabola
3. Find x-intercepts.
Let y = 0.
y = x2 – 2x – 3
0 = x2 – 2x – 3
0 = (x – 3)(x + 1)
(x – 3) = 0 → x = 3
(x + 1) = 0 → x = -1
Thus, graph passes through (3, 0) and (-1, 0)
Graphing Parabola
4. Find the y-intercept
Let x = 0 in the equation.
y = x2 – 2x – 3
y = 02 – 2(0) – 3 = -3
Thus, the parabola
passes through (0, -3)
5. Sketch the graph with
vertex, x-intercepts,
and y-intercept.
Your Turn
Graph the quadratic equation: y = x2 + 6x + 5
1. Upward or downward?
a = 1; b = 6; c = 5
Since a > 0, parabola opens upward.
2. Find the vertex.
−𝑏
−6
x=
=
= −3
2𝑎
2(1)
y = (-3)2 +6(-3) + 5
= 9 -18 + 5
= -4
vertex: (-3, -4)
Your Turn
3. Find the x-intercepts.
y = x2 + 6x + 5
Let y = 0
0 = x2 + 6x + 5
(x + 1)(x + 5) = 0
(x + 1) = 0 → x = -1
y = (-1)2 + 6(-1) + 5
y=1–6+5=0
x-intercepts:
(-1, 0) (-5, 0)
(x + 5) = 0 → x = -5
y = (-5)2 + 6(-5) + 5
y = 25 – 30 + 5 = 0
Your Turn
4. Find the y-intercepts.
y = x2 + 6x + 5
Let x = 0
Then, y = 5
y-intercept:
(0, 5)
5. Sketch the graph.
Vertex: (-3, -4)
x-intercepts: (-1,0)(-5,0)
y-interdept: (0, 5)
(0, 5)
(-5,0)
(-1,0)
(-3, -4)
Your Turn
• Given the quadratic equation: y = -x2 + 4x – 3
• Determine the following and graph the equation
of the parabola.
a)
b)
c)
d)
e)
Does the parabola open upward or downward?
Find the vertex.
Find the x-intercepts
Find the y-intercept.
Graph the quadratic equation.
Solution
•
•
•
•
Opens downward
Vertex: (2, 1)
X-intercepts: (0, 1) (0, 3)
Y-intercept: (-3, 0)