* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Population Growth Curves
Storage effect wikipedia , lookup
Human overpopulation wikipedia , lookup
Two-child policy wikipedia , lookup
The Population Bomb wikipedia , lookup
World population wikipedia , lookup
Molecular ecology wikipedia , lookup
Human population planning wikipedia , lookup
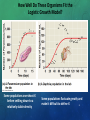
Ecology: Population Ecology POPULATIONS 3. A population is a group of individuals of the same species living in an area 2 DISTRIBUTION PATTERNS Populations disperse in a variety of ways that are influenced by environmental and social factors • Uniform distribution results from intense competition or antagonism between individuals. • Random distribution occurs when there is no competition, antagonism, or tendency to aggregate. • Clumping is the most common distribution because environmental conditions are seldom uniform. 3 What causes these populations of different organisms to clump together? Clumped distribution in species acts as a mechanism against predation as well as an efficient mechanism to trap or corner prey. It has been shown that larger packs of animals tend to have a greater number of successful kills. Fig. 52.1, Campbell & Reece, 6th ed. POPULATION DISPERSAL • In rare cases, long-distance dispersal can lead to adaptive radiation • For example, Hawaiian silverswords are a diverse group descended from an ancestral North American tarweed 5 THE SPREAD OF THE AFRICANIZED HONEY BEE WHEN DID THEY FIRST ARRIVE IN THE AMERICAS? HOW LONG DID IT TAKE FOR THEM TO EXPAND THEIR RANGE INTO THE US? HOW CAN YOU EXPLAIN THEIR SUCCESS IN EXPANDING THEIR 6 TERRITORY? SMALL GEOGRAPHIC RANGE 7 SPECIES WITH A LARGE GEOGRAPHIC RANGE 8 ESTIMATING POPULATION SIZE THE MARK-AND-RECAPTURE TECHNIQUE 2. 1. 3. 9 ESTIMATING POPULATION SIZE THE MARK-AND-RECAPTURE TECHNIQUE • There’s a simple formula for estimating the total population size 𝑠 𝑥 = 𝑁 𝑛 s = Number of individuals marked and released in 1st sample x = Number of individuals marked and released in 2nd sample n = Total number of individuals in 2nd sample N = Estimated population size Rearrange to get: 𝑁= 𝑠𝑛 𝑥 10 LET’S TRY AN EXAMPLE! • Twenty individuals are captured at random and marked with a dye or tag and then are released back into the environment. • Therefore s = # of animals marked = 20 • At a later time a second group of animals is captured at random from the population. Some will already be marked, say 10 individuals were marked out of 35 that were captured the second time. We now know n = 35 and x = 10 𝑠𝑛 • Remember: 𝑁= 𝑥 11 • So, apply the formula and solve for the estimated population size: 𝑁= 𝑠𝑛 𝑥 = 20 35 10 = 700 = 10 70 Therefore, N = 70 as a population estimate 12 WHICH METHOD WOULD YOU USE? 1. To determine the number of deer in the state of Virginia? 2. To determine the number of turkeys in a county? 3. To determine the number of dogs in your neighborhood? 4. To determine the number of ferrel cats in your neighborhood? 13 SURVIVORSHIP CURVES 1000 What do these graphs indicate regarding species survival rate & strategy? Human (type I) I. High death rate in post-reproductive years Hydra (type II) Survival per thousand 100 II. Constant mortality rate throughout life span Oyster (type III) 10 1 0 25 50 75 Percent of maximum life span 100 III. Very high early mortality but the few survivors then live long (stay reproductive) POPULATION GROWTH CURVES 𝑑𝑁 =𝐵−𝐷 𝑑𝑡 d = delta or change N = population Size t = time B = birth rate D =death rate r= 𝐵 −𝐷 𝑁 15 POPULATION GROWTH MODELS Exponential model (blue) idealized population in an unlimited environment (J-curve); can’t continue indefinitely. r-selected species (r = per capita growth rate) 𝒅𝑵 = 𝒓𝒎𝒂𝒙 𝑵 𝒅𝒕 Logistic model (red) considers population density on growth (S-curve), carrying capacity (K): maximum population size that a particular environment can support; K-selected species 𝒅𝑵 𝑲−𝑵 = 𝒓𝒎𝒂𝒙 𝑵 𝒅𝒕 𝑲 EXPONENTIAL GROWTH CURVES Growth Rate of E. coli d = delta or change N = Population Size t = time rmax = maximum per capita growth rate of population Population Size, N 𝒅𝑵 = 𝒓𝒎𝒂𝒙 𝑵 𝒅𝒕 Time (hours) 17 LOGISTIC GROWTH CURVES • In the logistic population growth model, the per capita rate of increase (rmax) declines as carrying capacity (K) is reached • The logistic model starts with the exponential model and adds an expression that reduces per capita rate of increase as N approaches K 𝑑𝑁 𝐾−𝑁 = 𝑟𝑚𝑎𝑥 𝑁 𝑑𝑡 𝐾 18 LOGISTIC GROWTH CURVES 𝒅𝑵 𝑲−𝑵 = 𝒓𝒎𝒂𝒙 𝑵 𝒅𝒕 𝑲 d = delta or change N = Population Size t = time K =carrying capacity rmax = maximum per capita growth rate of population 19 COMPARISON OF GROWTH CURVES 20 GROWTH CURVE RELATIONSHIP 21 EXAMINING LOGISTIC POPULATION GROWTH 22 EXAMINING LOGISTIC POPULATION GROWTH Hypothetical Example of Logistic Growth Curve K = 1,000 & rmax = 0.05 per Individual per Year 23 POPULATION REPRODUCTIVE STRATEGIES • r-selected (opportunistic) • Short maturation & lifespan • Many (small) offspring; 1 (early) reproduction; • No parental care • High death rate • K-selected (equilibrial) usually • Long maturation & lifespan • Few (large) offspring; usually several (late) reproductions • Extensive parental care • Low death rate How Well Do These Organisms Fit the Logistic Growth Model? Some populations overshoot K before settling down to a relatively stable density Some populations fluctuate greatly and make it difficult to define K 25 Age Structure Diagrams: Always Examine The Base Before Making Predictions About The Future Of The Population Rapid growth Afghanistan Male Female 10 8 6 4 2 0 2 4 6 Percent of population Age 85+ 80–84 75–79 70–74 65–69 60–64 55–59 50–54 45–49 40–44 35–39 30–34 25–29 20–24 15–19 10–14 5–9 0–4 8 10 8 Slow growth United States Male Female 6 4 2 0 2 4 6 Percent of population Age 85+ 80–84 75–79 70–74 65–69 60–64 55–59 50–54 45–49 40–44 35–39 30–34 25–29 20–24 15–19 10–14 5–9 0–4 8 8 No growth Italy Male Female 6 4 2 0 2 4 6 8 Percent of population