Download b - Catawba County Schools

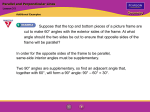
8th Grade Math Ch. 10 Review
Define and sketch a pair of each type of lines:
Perpendicular
Coincidental
Intersecting but not perpendicular
Parallel
Define the following:
Skew lines
Coplanar
Adjacent angles
Fill in the blank with the correct term.
An angle that measures 90 degrees is a __________ angle.
Two angles whose sum is 180 degrees are ______________________ angles.
Adjacent angles can be (supplementary, congruent, or both).
Linear pairs of angles are always (supplementary or congruent).
Lines a and b are parallel. Line c is the transversal.
Identify all of the pair of angles for each type below. Then determine if those type of angles
are congruent or supplementary.
c
1
a
2
3
5
b
4
6
7
8
Vertical angles:
Same-side interior angles:
Alternate interior angles:
Alternate exterior angles:
Corresponding angles:
Same-side exterior angles:
1. In the figure shown,
seven angles in the figure.
. If the measure of angle 7 is 49 degrees, determine the measures of the other
c
1
a
3
5
b
7
2
4
6
8
2. Use slopes to determine whether the two lines are parallel, perpendicular, or neither.
3. Use slopes to determine whether the two lines are parallel, perpendicular, or neither.
4. Use slopes to determine whether the two lines are parallel, perpendicular, or neither.
6y = 2x – 24
-6y = -12x + 10
5. Consider the points C(3, 6) and D(2, 4). Graph line CD and label.
a.
Determine the slope of line CD.
b.
Points
and
are formed by
translating C and D right 5 units. Graph
line C’D’. Determine the coordinates of
and .
c.
Determine the slope of line
d.
How are lines CD and
Explain.
The map shows a portion of downtown Mapledale. Use the map to answer each question.
6. Which streets on the map appear to be parallel?
7. Which streets on the map appear to be perpendicular?
.
related?
In each figure shown, determine the measures of the marked angles.
8.
9. Use origin as the point of rotation and rotate line AB 90 counterclockwise to form line A’B’. Calculate the
slope of each line to determine if the lines are perpendicular. Explain how you determined your answer.
Reflect line segment AB over the reflection line to form line segment CD. Reflect line segment EF over the
reflection line to form line segment GH. Calculate the slopes of all line segments to prove that the line
segments are parallel.
10.