Download Confidence Interval Module - Naval Postgraduate School

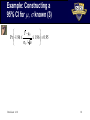
Module 5: Interval Estimation
Statistics (OA3102)
Professor Ron Fricker
Naval Postgraduate School
Monterey, California
Reading assignment:
WM&S chapter 8.5-8.9
Revision: 1-12
1
Goals for this Module
• Interval estimation – i.e., confidence intervals
– Terminology
– Pivotal method for creating confidence intervals
• Types of intervals
– Large-sample confidence intervals
– One-sided vs. two-sided intervals
– Small-sample confidence intervals for the mean,
differences in two means
– Confidence interval for the variance
• Sample size calculations
Revision: 1-12
2
Interval Estimation
• Instead of estimating a parameter with a
single number, estimate it with an interval
• Ideally, interval will have two properties:
– It will contain the target parameter q
– It will be relatively narrow
• But, as we will see, since interval endpoints
are a function of the data,
– They will be variable
– So we cannot be sure q will fall in the interval
Revision: 1-12
3
Objective for Interval Estimation
• So, we can’t be sure that the interval
contains q, but we will be able to
calculate the probability the interval
contains q
• Interval estimation objective: Find an
interval estimator capable of generating
narrow intervals with a high probability
of enclosing q
Revision: 1-12
4
Why Interval Estimation?
• As before, we want to use a sample to infer
something about a larger population
• However, samples are variable
– We’d get different values with each new sample
– So our point estimates are variable
• Point estimates do not give any information about
how far off we might be (precision)
• Interval estimation helps us do inference in such a
way that:
– We can know how precise our estimates are, and
– We can define the probability we are right
Revision: 1-12
5
Terminology
• Interval estimators are commonly called
confidence intervals
• Interval endpoints are called the upper
and lower confidence limits
• The probability the interval will enclose
q is called the confidence coefficient or
confidence level
– Notation: 1-a or 100(1-a)%
– Usually referred to as “100(1-a)” percent CIs
Revision: 1-12
6
Confidence Intervals: The Main Idea
• Via the CLT, we know that Y is within 2 std
errors ( Y n ) of m 95% of the time
• So, m must be within 2 SEs of Y 95% of the time
(Unobserved) sampling
distribution of the mean
y
(Unobserved) mY
95% confidence
interval for mY
(Unobserved) population
distribution (pdf of Y)
mY  2 Y
n
7
In General
• A two-sided confidence interval:
Lower confidence
limit

Upper confidence
limit

Pr qˆL  q  qˆU  1  a
Target
parameter
Confidence
coefficient
• A lower one-sided confidence interval:


Pr qˆL  q  1  a
• An upper one-sided confidence interval:
Pr q  qˆU   1  a
Revision: 1-12
8
Pivotal Method: A Strategy
for Constructing CIs
• Pivotal method approach
– Find a “pivotal quantity” that has following two
characteristics:
• It is a function of the sample data and q, where
q is the only unknown quantity
• Probability distribution of pivotal quantity does
not depend on q (and you know what it is)
• Now, write down an appropriate probability
statement for the pivotal quantity and then
rearrange terms…
Revision: 1-12
9
Example: Constructing a
95% CI for m,  known (1)
• Let Y1, Y2, …, Yn be a random sample from a
normal population with unknown mean mY and
known standard deviation Y
• Create a CI for mY based on the sampling
2
distribution of the mean: Y ~ N mY ,  Y / n
• To start, we know that (via standardizing):


Y  mY
~ N (0,1)
Y / n
Revision: 1-12
10
Example: Constructing a
95% CI for m,  known (2)
• Now for Z ~ N(0,1) we know
Pr(1.96  Z  1.96)  0.95
– That is, there is a 95% probability that the random
variable Z lies in this fixed interval
• Thus


Y - mY
Pr  -1.96 
 1.96   0.95
Y / n


• So, let’s derive a 95% confidence interval…
Revision: 1-12
11
Example: Constructing a
95% CI for m,  known (3)


Y - mY
Pr  -1.96 
 1.96   0.95
Y / n


Revision: 1-12
12
Example: Constructing a
95% CI for m,  known (4)
• So, If Y1 = y1, Y2 = y2, …, Yn = yn are observed
2
values of a random sample from a N m , 
with  known, then

Y
y  1.96
n

is a 95% confidence interval for mY
• We can be 95% confident that the interval
covers the population mean
– Interpretation: In the long run, 19 times out of 20
the interval will cover the true mean and 1 time out
of 20 it will not
Revision: 1-12
13
Calculating a Specific CI
• Consider an experiment with sample size
n=40, y  5.426 and Y=0.1
• Calculate a 95% confidence interval for mY
Revision: 1-12
14
Example 8.4
• Suppose we obtain a single observation Y
from an exponential distribution with mean q.
Use Y to form a confidence interval for q with
confidence level 0.9.
• Solution:
Revision: 1-12
15
Example 8.4 (continued)
Revision: 1-12
16
Example 8.5
• Suppose we take a sample of size n=1 from a
uniform distribution on [0,q ], were q is
unknown. Find a 95% lower confidence
bound for q.
• Solution:
Revision: 1-12
17
Example 8.5 (continued)
Revision: 1-12
18
Large-Sample Confidence Intervals
• If q̂ is an unbiased statistic, then via the CLT
qˆ  q
Z
qˆ
has an approximate standard normal
distribution for large samples
• So, use it as an (approximate) pivotal quantity
to develop (approximate) confidence intervals
for q
Revision: 1-12
19
Example 8.6
• Let qˆ ~ N (q, qˆ ) . Find a confidence interval
for q with confidence level 1-a.
• Solution:
Revision: 1-12
20
Example 8.6 (continued)
Revision: 1-12
21
One-Sided Limits
• Similarly, we can determine the 100(1-a)%
one-sided confidence limits (aka confidence
bounds):
– 100(1  a)% lower bound for q  qˆ  zaqˆ
– 100(1  a)% upper bound for q  qˆ  zaqˆ
• What if you use both bounds to construct a
two-sided confidence interval?
– Each bound has confidence level 1-a, so resulting
interval has a 1-2a confidence level
Revision: 1-12
22
Example 8.7
• The shopping times of n=64 randomly
selected customers were recorded with y  33
minutes and s y2  256. Estimate m, the true
average shopping time per customer with
confidence level 0.9.
• Solution:
Revision: 1-12
23
Example 8.7 (continued)
Revision: 1-12
24
Example 8.8
• Two brands of refrigerators, A and B, are
each guaranteed for a year. Out of a random
sample of nA=50 refrigerators, 12 failed before
one year. And out of an independent random
sample of nB=60 refrigerators, 12 failed before
one year. Give a 98% CI for pA-pB.
• Solution
Revision: 1-12
25
Example 8.8 (continued)
Revision: 1-12
26
Example 8.8 (continued)
Revision: 1-12
27
What is a Confidence Interval?
• Before collecting data and calculating it, a confidence
interval is a random interval
– Random because it is a function of a random variable (e.g., Y )
• The confidence level is the long-run percentage of
intervals that will “cover” the population parameter
– It is not the probability a particular interval contains the
parameter!
• This statement implies that the parameter is random
• After collecting the data and calculating the CI
the interval is fixed
– It then contains the parameter with probability 0 or 1
Revision: 1-12
28
A CI Simulation
• Simulated 20 95%
confidence intervals
with samples of size
n=10 drawn from
N(40,1) distribution
• One failed to cover
the true (unknown)
parameter, which is
what is expected on
average
Revision: 1-12
29
Another CI Simulation
• Simulated 100 95%
confidence intervals
with samples of size
n=10 drawn from
N(40,1) distribution
• 6 failed to cover the
true (unknown)
parameter
– Close to the
expected number: 5
Revision: 1-12
30
Illustrating Confidence Intervals
This is a demonstration showing confidence
intervals for a proportion.
TO DEMO
Applets created by Prof Gary McClelland, University of Colorado, Boulder
You can access them at
www.thomsonedu.com/statistics/book_content/0495110817_wackerly/applets/seeingstats/index.html
Revision: 1-12
31
Summary: Constructing a Two-sided
Large-Sample Confidence Interval
• For an unbiased statistic qˆ , determine  qˆ
• Choose the confidence level: 1-a
• Find za /2
– E.g., for a = 0.05, z0.025  1.96
• Given data, calculate qˆ and  qˆ
• Then the 100(1-a)% confidence interval for q is
qˆ  za /2 ˆ ,qˆ  za /2 ˆ 
q
q

Revision: 1-12
32
E.g., Constructing a Two-sided
Large-Sample 95% CI for m
• Y is an unbiased estimator for m, and we
know  Y   Y n
The confidence level is 1-a = 0.95
• So za /2  z0.025  1.96
• Given data, calculate y and the 95% CI for m
is
 y  1.96 Y

Revision: 1-12
n , y  1.96 Y
n 
33
E.g., Constructing a Two-sided
Large-Sample 95% CI for p
• For Y, the number of successes out of n trials,
an unbiased estimator for p is pˆ  Y / n
• Then note that  pˆ  p(1  p) / n
– Follows from: Var(Y / n)  Var(Y ) / n2  np(1  p) / n 2
– And, since we don’t know p, ˆ pˆ 
pˆ (1  pˆ ) / n
• As before, for a confidence level of 1-a =
0.95, za /2  z0.025  1.96
• So, the 95% CI for m is
 pˆ  1.96 pˆ 1  pˆ  n , pˆ  1.96 pˆ 1  pˆ  n 


Revision: 1-12
34
How Confidence Intervals Behave
• Width of CI’s: w  2  za /2 
• Margin of error: E  za /2 
Y
n
Y
n
– Bigger s.d.  bigger s.e.  wider intervals
– Bigger sample size  smaller s.e.  narrower
intervals
– Higher confidence  bigger z-values  wider
intervals
Revision: 1-12
35
Sample Size Calculations
• Often desire to determine necessary sample
size to achieve a particular error of estimation
– Must specify the estimation error B and know or
well estimate the population standard deviation 
• Then for a 100(1-a)% two-sided CI solve
B  za /2 
for n:
Revision: 1-12

n
 za /2 
n

w


2
36
Example
• We want to estimate the average daily yield m
of a chemical, where we know =21 tons
• Find the sample size (n) so that a 95% CI for
m has an error of estimation to be less than
B=5 tons
Revision: 1-12
37
Example 8.9
• A stimulus reaction may take two forms: A or
B. If we want to estimate the probability the
reaction will be A, what sample size do we
need if
– We want the error of estimation less than 0.04
– The probability p is likely to be near 0.6
– And we plan to use a confidence level of 90%
• Solution:
Revision: 1-12
38
Example 8.9 (continued)
Revision: 1-12
39
Example 8.10
• We’re going to compare the effectiveness of
two types of training (for an assembly op)
– Subjects to be divided into 2 equally sized groups
– Measurement range expected to be about 8 mins
– Estimate mean difference in assembly time to
within 1 minute with 95% confidence
• Solution:
Revision: 1-12
40
Example 8.10 (continued)
Revision: 1-12
41
Small-Sample Confidence
Interval for m ( Unknown)
• For small n and  unknown, standardized
statistic no longer normally distributed
• But, if Y is the mean of a random sample of
size n from a distribution with mean m,
Y m
T  n 1 
s/ n
has a t distribution with n-1 degrees of freedom
– Precisely if population has normal distribution
• See Theorems 7.1 & 7.3 and Definition 7.2
– Approximately for sample mean via CLT
Revision: 1-12
42
Very Similar to Confidence
Interval for m with  Known
• So, we can use the t distribution to build a CI!
• Deriving using T as the pivotal quantity:


Y m
Pr  ta /2,n1  T n 1  ta /2,n 1   Pr  ta /2,n 1 
 ta /2,n 1 
s/ n



 Pr Y  t
 Pr ta /2,n 1s / n  Y  m  ta /2,n 1s / n
a /2, n 1
Revision: 1-12

s / n  m  Y  ta /2,n1s / n
43

So, Constructing a 95% Confidence
Interval for m (with  Unknown)
• Choose the confidence level: 1-a
• Remember the degrees of freedom () = n -1
• Find ta / 2, n 1
– Example: if a = 0.05, df=7 then t0.025, 7 = 2.365
• Calculate y and s / n
• Then the 95% confidence interval for m is
s
s 

, y  2.365 
 y  2.365
n
n

Revision: 1-12
Remember, this value also depends on the dfs
44
Example 8.11
• A manufacturer of gunpowder has developed
a new powder. Eight tests gave the following
muzzle velocities in feet per second:
3,005
2,925
2,935
2,965
2,995
3,005
2,937
2,905
Find a 95% CI for the true average velocity m
• Solution:
Revision: 1-12
45
Example 8.11 (continued)
Revision: 1-12
46
Small-Sample Confidence
Interval for m1-m2
• Suppose we want to compare the means of
two normally distributed populations
– Population 1: mean m1 ,
– Population 2: mean m2 ,
• Then
Y Y   m

Z
1
2
 12
n1
1

variance 12
variance  22
 m2 
 22
~ N (0,1)
n2
• Can use this as a pivotal quantity
Revision: 1-12
47
Small-Sample Confidence
Interval for m1-m2 , continued
2
2
2
• If we can further assume that 1   2   , then
Y Y   m

Z
1
2
1
 m2 
1 1


n1 n2
~ N (0,1)
• But if  is unknown, then need to appropriately
estimate it
• To do so, first estimate the two sample means
n1
Revision: 1-12
1
Y1   Y1i
n1 i 1
n2
1
Y2   Y2i
n2 i 1
48
Pooled Estimate of the Variance
• Then, the pooled estimate of variance:
Sample mean for
population Y1
2
(
y

y
)

(
y

y
)
 i 1 1i 1  i 1 2i 2
n1
s 2p 
Sample mean for
population Y2
Average squared deviation
from different means
2
n2
n1  n2  2
2
1
• Can also express as a weighted average of s
and s22 :
2
2
(n1  1) s1  (n2  1) s2
s 
n1  n2  2
2
p
Revision: 2-10
49
Small-Sample Confidence
Interval for m1-m2 , continued
2
2
2
• So, assuming 1   2   , we have
 Y1  Y2    m1  m2  
Z


W /    1 n1   1 n2  
Y Y   m


1
2
Sp
Revision: 1-12
1
 m2 
1 1

n1 n2
2
n

n

2
S
1 2  p
 2  n1  n2  2 
~ T  n 1
50
Example 8.12
• Lengths of time for two groups of employees
to assemble a device:
Training
Type
Time to Assemble
Measurements
Standard
32
37
35
28
41
44
35
31
34
New
35
31
29
25
34
40
27
32
31
– Standard: Employees received standard training
– New: Employees received a new type of training
• Estimate the true mean difference in training
(m1-m2) with 95% confidence
Revision: 1-12
51
Example 8.12 Solution
Revision: 1-12
52
Example 8.12 (continued)
Revision: 1-12
53
CI for the Variance
• Let X1, X2, …, Xn be a random sample from a
normal population with mean m and standard
deviation 
• Consider the the pivotal quantity
 2

(n  1) S 2
2
Pr  1a /2,n1 
 a /2,n1   1  a
2



• Then a confidence interval for the variance is:
2 
 (n  1) S 2
(
n

1)
S
Pr  2
2  2
 1 a

 


a
/2,
n

1
1

a
/2,
n

1


Revision: 1-12
54
Example: 95% CI for Variance
• After observing s2 = 25.4 for n=20 obs, calculate a
95% CI for  2
– For =19, chi-squared critical values are 8.906 and 32.852
– So:
 (n  1) s 2
(n  1) s 2 
Pr  2
2  2
  1  a
 
1a /2,n 1 
 a /2,n 1
19  25.4 
 19  25.4
or, 
2 
  0.95
8.906 
 32.852
Thus, the 95% CI  [14.69, 54.19
• Remember, the distribution is not symmetric, so be
careful with a and a
– Lower limit divides by the bigger critical value
Revision: 1-12
55
Example 8.13
• We want to assess the variability of a
measuring methodology. Three independent
measurements are taken: 4.1, 5.2, and 10.2.
Estimate 2 with confidence level 90%.
• Solution:
Revision: 1-12
56
Example 8.13 (continued)
Revision: 1-12
57
Why Calculate CIs for ?
• Just like with m,  is a population parameter
– Sometimes need to know how well it is estimated
by s
• E.g., the precision of a weapon is inversely
proportional to its standard deviation – if the
standard deviation is large, the weapon is not
precise
– Confidence intervals for  provide information
about the likely range of the impact error
– Big difference between a  of 3 meters and a  of
300 meters with implications for both collateral
damage and friendly troops
Revision: 1-12
58
Bootstrap Confidence Intervals
• Can use the bootstrap method to estimate
confidence intervals
• Basic idea:
– Use bootstrap methodology to create an empirical
sampling distribution for statistic of interest
– Then take the appropriate quantiles of the
empirical distribution for upper and lower endpoints of confidence interval
• As with point estimation, useful when it’s hard
to analytically specify sampling distribution
Revision: 1-12
59
Caution! Confidence Intervals
are Not for Prediction
• CI is an interval estimate for the population
parameter
• CIs do not predict the likely range of the next
observation - common pitfall!
• Interval for next observation is called a
prediction interval
• Prediction interval has variability of original
random variable plus the uncertainty about
the population parameter
Revision: 1-12
60
What We Covered in this Module
• Interval estimation – i.e., confidence intervals
– Terminology
– Pivotal method for creating confidence intervals
• Types of intervals
– Large-sample confidence intervals
– One-sided vs. two-sided intervals
– Small-sample confidence intervals for the mean,
differences in two means
– Confidence interval for the variance
• Sample size calculations
Revision: 1-12
61
Homework
• WM&S chapter 8.5-8.9
– Required exercises: 40, 41, 42, 60, 63, 64, 71,
82, 91, 96
– Extra credit: 94
• Useful hints:
 Problems 8.91 and 8.96: Here’s you’re given the
raw data and must calculate the necessary
statistics first
Revision: 1-12
62