Download Math 190 sample final S2009 - Department of Mathematics, CCNY

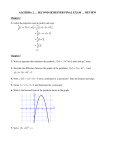
Instructions: Show all work. You may use a scientific calculator.
There are 4 parts. In each part choose 5 questions. Each question is worth
5 points.
In your answer book, for each question you want graded:
 draw a box around the answer, and
 write the number of the question inside or next to the box.
Part I. Choose any 5 questions from this part.
1) Find both the radius and an equation of the circle with center (2,–3) that passes through the
point (-1, 1).
2) Find an equation of the line through point (7, 6) that is perpendicular to the line 2 x  5 y  13 .
f ( x  h)  f ( x  h)
h
8 x3  4 x 2  5 x  1
4) Use long division to simplify the fraction
.
x 1
1
1

5) Rewrite x  2 x as a completely reduced fraction.
4x  4
3) Given f ( x)  3  x2 simplify
x3  2 x 2
6) Find the center and radius of the circle whose equation is x2  y 2  10  y  2 x .
Part II. Choose any 5 questions from this part.
7)
x y 
 y x 3 


Simplify ( xy 2 ) 3 
3
1
2
so that only positive powers appear in your answer.
2 x  2 y  2 z  3

8) Use Cramer’s rule to solve for x. Do not solve for y or z:  x
 2 z  3
2 x  y  2 z  1

50u11v11  u 2v3 32u 7v5 so that your answer involves just one square root sign.
3 y  x  5
10) Solve the system of equations:  2
2
 x  y  3
9) Simplify
11) The product of two negative numbers is 48. One number is two more than the other number.
Find the numbers.
12) Solve the equation 2 x  1  3  x  4 for x and check your answer(s).
Math 19000
Final Examination , page 2
Fall 2006
Part III. Choose any 5 questions from this part.
13)
Solve the equation x 2  3x for x.
14) In triangle ABC, angle C measures 80 degrees, angle B measures 30 degrees, and the length
of side BC is 6. Find the length of side AC, correct to 3 decimal places.
15)
A is an acute angle with tan(A) =
2
.
5
Find the exact value of sin(A). You may leave
square roots in your answer.
16) In triangle ABC, angle A measures 20 degrees, side AC measures 10 centimeters, and the
length of side AB is 12 centimeters. Find the length of side BC, correct to three decimal places.
17) Sketch the graph of the parabola y  x2  4x  3 by first finding and labeling the coordinates of its vertex and intercept(s).
18)
Solve:
1
x
2

1
6
for x.

x x2
Part IV. Choose any 5 questions from this part.
19) Rewrite
20) Rewrite
2x  1
x
as a completely reduced fraction.

2
x  x x 1
x6  x 2
( x3  x) 2
as a completely reduced fraction.
21) Given the function g ( x)  x  x2 , find and simplify the expression g (3  x)  g ( x  3).
3  x x2  9
and write your answer as a completely reduced fraction.

2  x x2  4
2
23) Rewrite
as an expression that doesn’t involve a fraction.
5 3
24) Given functions f ( x)  1  x 2 and h( x)  2  x find and simplify
a) h( f ( x )) and b) f (h( x)).
22) Work out
End of exam.
Math 195 CLOs
1. solve rational equations and inequalities in one real variable;
2. graph linear, polynomial, trigonometric, exponential, and logarithmic equations;
3. work with transformations of, and translate between, graphs and equations;
4. determine whether a graph is the graph of a function;
5. demonstrate fluency with function notation, including composite and inverse functions;
6. construct a quadratic polynomial model of appropriate real-world problems;
7. find maximum /minimum values for a quadratic function and apply to optimization problems;
8. state and apply trigonometric identities;
9. represent and solve real-world problems involving exponential growth and decay; and
10. solve other problems appropriate for a course in pre-calculus
NOTE: CLO 4 is MISSING FROM THE FOLLOWING EXAM.