Download Solutions

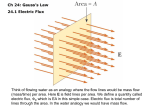
PHYS260 (Gupta) SOLUTIONS TO HW9 Contributed by Colleen, Eric, and me.
This week’s HW is on Gauss’s Law. The next exam is on Nov 24th. It would cover the
topics of Charge, Coulomb’s Law, Field, and Gauss’s Law - HWs
7,8,9
1. The picture shows three disks in an electric field. Disks A and B
are the same size. C is larger.
(a) At which disk is the electric field strongest? Second strongest?
Weakest? Explain.
B A
The field information here is provided by the electric field lines.
C
Where the lines are bunched together, the field is stronger; if the
lines are diffuse the field is weaker (And the direction of the field
is always tangent to the field lines). Now for A and B, the field
lines are equally bunched up. The field lines are exactly the same for
A and B (even though B is slanted). And so the field at A and B is the same. The field
lines spread out at C, and so the field there must be weaker. And so, Field is strongest at
disks A and B; weaker at C.
Note: For the field, it does not matter that disk C is larger, or that disk B is at an angle.
The field is the influence of the source charge distribution (which is not shown here). It
does not depend on what is “feeling” that field. In doing this, we are assuming that the
field lines shown depict the final total field being experienced by the disks.
(b)Through which disk is the flux greatest? Second greatest? Smallest? Explain.
Now the disks matter. Flux is the ‘total amount of field crossing the disk, or being
intercepted by the disk’. Using this idea, I can quickly see that disk B intercepts less
field than disk A because it is at an angle. Because of the angle less of the field “crosses”
disk B. Disk C on the other hand intercepts exactly the same amount of field as A. We
can see that the lines that are on the boundary of disk A are also on the boundary of disk
C. So all the flux through A also passes through C. So for flux:
Flux-A = Flux-C > Flux-B
What about the fact that disk C is larger? Shouldn’t it have a larger flux, especially since
Flux = (Field)*(Area) ? True that disk C is larger, but that is precisely why it was possible
for Flux-A to equal Flux-C. The field at C is more spread out then at A. In order for the
flux at C to equal flux at A -- in other words, for the same “amount” of field to cross
diskC -- diskC has to be larger. The larger size of C compensates for the spreading out of
the field. How do we know that the compensation is perfect? -- We know that because
the field lines that are on the boundary of A, are also exactly on the boundary of C ...
PHYS260 (Gupta) SOLUTIONS TO HW9 Contributed by Colleen, Eric, and me.
2. A glass window of width W = 2.0 meters and height H = 1.0 meter is rubbed so as to
give the window a total charge of Q = 2.00 µC, spread uniformly over its surface.
Consider three possible Gaussian surfaces a student might use to try to find the electric
field a distance 5.0 cm from the window: (a) a sphere, (b) a cylinder, and (c) a
rectangular “box.”
(a) Using the spherical Gaussian sphere surface, can you find the electric field at a
point 5 cm away from the window, right at the center of the window-rectangle? If
so, do it, explaining your reasoning step by step. If not, explain why the Gaussian
sphere doesn’t “work.”
(b) Using the Gaussian cylinder, can you find the electric field 5.0 cm from the
window? If so, do it, explaining your reasoning step by step. If not, explain why
the Gaussian cylinder doesn’t “work.”
(c) Does the rectangular “box” enable you to use Gauss' Law to solve for the electric
field? Without actually solving for E, explain why this Gaussian “box” works or
doesn’t work, referring back to parts (a) and (b) to support your reasoning.
Okay; So first, the picture of the surface looks like this: (Note that P is very close to the
window pane compared to the dimensions of the widow pane)
The field looks like:
It is uniform around P. It
points up on the top of the window-pane and down on the bottom. And it is
perpendicular to the window pane.
Now To find the field at P, I would need to first consider a Gaussian Surface passing
through P. If I can easily relate the field at P to the flux through the Gaussian Surface,
then using Gauss’s Law, I can find a simple relation between the field at P and the
charge enclosed by the surface and thus find the field at P:
Relate Flux to Field at P: need
this to be a simple relation.
Gaussʼs Law: The flux through the Gaussian
surface = (charge enclosed)/(ε0)
Use these two to then find the field at P!
PHYS260 (Gupta) SOLUTIONS TO HW9 Contributed by Colleen, Eric, and me.
(a) Now if I chose the spherical Gaussian surface: Here is what it would look like:
since the field is all vertical, different
portions of the sphere would be at a different angle to the field. The first task is to relate


the field and the flux through the surface. Flux, Φ = ∫ E • dA = ∫ E cosθ dA where θ is
Sphere
sphere
the angle between the field vector and the area vector. Now because of the shape of the
sphere, every little patch of area, dA on the sphere would have a different angle with
the field vector and so it would be very difficult to compute this integral, defeating the
purpose of using Gauss’s Law.
(b) If I draw a cylinder as the Gaussian surface through P, it could look like this:
P
*
Again, the same problem as the sphere. Different
parts of the curved surface of the cylinder make different angles with the field making it
difficult to find a simple relation between the field and the flux.
BUT I could also draw the cylinder like this:
P
*
Now things are looking better. Everywhere, on the flat end-caps of the cylinder, the field
is perpendicular. On the curved walls of the cylinder the field is parallel to the surface,
everywhere. The area vectors on the cylinder look like this:
The area vectors always point out from the enclosed volume.
PHYS260 (Gupta) SOLUTIONS TO HW9 Contributed by Colleen, Eric, and me.
So on top end-cap of cylinder, the E*dA = Ecos(0)dA=EdA; On bottom end-cap
similarly, E*dA = Ecos(0)dA=EdA (Note, both the field vector and area vector are
pointing down now). For the sides, look at the dark patch of area. The area vector is
horizontal, while the field vector is vertical! and so for all patches of area on the curved
walls of the cylinder: E*dA = Ecos(90)dA=0 ! The sides of the cylinder make no
contribution to the flux.
And we knew that already: We know that no field lines are ‘crossing’ the side walls they are all parallel to the side-walls, so the flux through the side walls has to be zero.
On the top end of the cylinder then flux contribution is
 
Φ = ∫ EidA = ∫ E dA = E ∫ dA =EA where A is the area of the top end of the cylinder and
top
flat
end
top
flat
end
top
flat
end
E is the constant field on top. If I consider the cylinder to go as much on top as on
bottom of the window-pane, then the field on the top flat end is same in magnitude as
the field on the bottom flat end. And so the contribution from the bottom end is also EA.
Total flux through the cylinder: Φ cylinder = Φ curved + Φ top + Φ bottom = 0 +EA+EA=2EA
walls
flat
part
flat
part
By Gauss’s law then, 2EA = (charge enclosed)/(ε0) or E = (charge enclosed/Area of
cylinder)/2ε0
Since the charge on the window pane is uniformly distributed:
charge enclosed by cylinder Total Charge on pane Qtotal
2 µC
µC
=
=
=
=1 2
Area of cylinder
Total Area of pane
Apane 1m × 2m
m
Substituting, we get, E(field at P) = 1/2ε0 µC/m2
σ
In general for a plane surface: E =
where σ is the surface charge density.
2ε 0
(c) For the box the picture looks like:
the situation is exactly the same as the cylinder stuff we
did before: since the field is parallel to the sides of the box and the top and bottom
contribute to the flux.
3. A rod of length L=1.00 meter carries λ = 2.0x10-9 C/cm of
charge throughout its length. The rod is lying on the floor.
Point A is on the rod, 40 cm from one of its ends. Point B is in
mid-air, a vertical distance hB = 4.0 cm above point A.
(a) Find the magnitude of the electric field at B,using Gauss'
Law. Work in symbols before you put in any numbers.
Solve this from scratch; don’t just use pre-derived equations about rods. [Hint: on
website]
Hint: All around B approximate the electric field as vertical (or more precisely
radially out from the rod). Why can I make this approximation? Well, the 40 cm of the
bar to the left and right of point A give horizontal components of E that cancel out. It’s
true that there is 20 cm at the right end of the bar that has gives a horizontal component
to the electric field, but think about the distances. Point B is 4 cm from Point A and is a
little more than 40 cm from the right end of the bar that gives a horizontal component.
This is like 10 times farther away. Since the electric field depends on distance like 1/R2,
this rough approximation says that the horizontal component of the electric field from
the right end of the bar is (at least) 100 times smaller than the vertical component. Also,
there more length of the bar (80 cm) contribute a vertical electric field at this point (and
these parts of the bar are closer), whereas only 20 cm of the bar contribute to the
horizontal component (and these parts are much farther from B). This isn’t exact, but
now I can justify approximating the electric field around B as being radially out from
the rod.
Now, I want to draw a Gaussian surface where the field around the surface is
constant. I can do this by drawing a thin, imaginary cylinder that is centered on the bar
and has point B on its surface. Since I am approximating the electric field as radially
away from the bar, I know that the angle between the electric field at the Gaussian
surface and the Area vector (which is perpendicular to the surface) is 0 degrees and that
the electric field strength should be roughly the same everywhere on the surface of the
cylinder, since (i) all points on the curved wall of the cylinder are the same distance
away from the rod and (ii) the length of the cylinder is small and so I can assume the
field to be constant along the length of the small cylinder.
No electric flux goes through the circular ends of the Gaussian cylinder, because
the electric field is perpendicular to the Area vector there and Cos(90 deg) = 0. Because
of the cosine of the angle between E and dA is 1 everywhere else through the cylinder
and the electric field strength is the same everyone on that surface, I can calculate the
total flux through the Gaussian cylinder with the electric field times the area: E (2 π L h),
where L is just the length of the cylinder and h is the distance from the rod. Also, the
charge inside my Gaussian cylinder is just the length of bar, L times the charge density,
λ. Gauss’ Law now says the following: E (2 π L h) = (λL)/ε0. Solving for E gives
E = λ / (2 π ε0 h).
(b) Point C is hC= 20 cm directly above point A. Could we use Gauss' Law to find the
electric field at that point? Explain why or why not.
Part of my argument for why I could approximate the electric field as radial at
point B was that the distance from point A and other points contributing only a vertical
component to the electric field were much closer than the 20 cm at the right end of the
bar, so that we estimated that the horizontal component of the electric field was at least
100 times smaller than the radial component, so we could approximate the electric field
there as radial.
Now, at point C, point A is 20 cm away and the point 20 cm from the right end of
the bar is about 45 cm away. This is about twice the distance, so from our distance
argument, the horizontal component of the field is about 1/4th of the vertical
component at point C. This is now too much of a horizontal component to approximate
the electric field as vertical at point C.
We can’t just draw a larger cylinder with point C on the surface, because the
electric field will make some angle with the Area vector that we won’t know, so we
don’t know what cosθ is. Also, some flux will now go through the circular ends of the
cylinder since the field will have some component in the x direction, but we don’t know
cosθ on this face of the cylinder either. Because of this, we won’t be able to use Gauss’
Law to find the field at C.
(c) Point D is hD = 1.0 cm above the left end of the rod. Could we use Gauss' Law to find
the electric field at that point? Explain why or why not.
Again the electric field will not be vertical. Here the reason
is because all points of the bar (except for the part right under
point D) will contribute a horizontal component to the electric
field. All of these horizontal components of the electric field
will add up whereas before only 20 cm of the bar that was
really far away was making a horizontal component of the
electric field. Because the electric field is at some angle, we
have the same problems as for point C in calculating the flux.
4. A solid cylindrical rod of length L and radius R (green) fits
snugly inside a “sheath,” shaped like a cylindrical shell (Cyan),
also of length L, inner radius = R, and outer radius, 3R. The
picture shows an end-on view. The rod contains total charge Q, spread uniformly over
its volume, while the sheath has a uniform charge density of σ per cubic centimeter.
Points A and B are located 0.75R and 2R, respectively from the central axis of the rod
(along the length of the rod, A and B are midway from either end).
(a) Is the electric field at point A the same or different from what it would be if the
sheath weren’t there? Explain.
We can draw a Gaussian cylinder that has point A on its surface. The cross section
of this looks like a circle like in the picture above. From Gauss’ Law, the total electric
flux through this surface is only due to the charge of the part of the green rod inside.
And so the field at A does not change whether the sheath is there or not.
How can it be that the charge of the Cyan sheath doesn’t contribute to the electric
field at A? Right in the center of the rod, the electric field from the sheath must cancel to
be zero, but what about at point A? Point A is closer to the top of the sheath than the
bottom, so it seems like the sheath should exert an electric field pointing down at point
A.
Well, one way to resolve this is to see that there is more parts of the sheath below
point A, so even though those parts of the sheath are farther away, there is more charge
exerting an electric field up. It must be that these two factors, distance and amount of
charge, balance out to cancel out the sheath’s electric field. The same reasoning can
resolve the fact that the charge of the rod outside the Gaussian cylinder doesn’t affect
the electric field. The charge inside the Gaussian cylinder is all below point A so
contributes an electric field pointing up at A.
(b) Is the electric field at point B the same or different from what it would be if the rod
weren’t there? Explain.
If you take the rod away, then that’s some charge that was all below B that is no
longer exerting an electric field at that point. Unlike the sheath in part a), the rod’s
contribution to the electric field at B is not zero, so taking it out will change the electric
field at B.
We can see this with Gauss’ Law since removing the rod will decrease the amount
of charge inside the Gaussian cylinder, changing the electric flux through the cylinder.
5. Same set up as the previous question#4.
(a) Find the electric field strength at point A.
Draw the Gaussian cylinder that has point A on its surface and has length l. The
field at point A points straight up. The electric field around point A is approximately
vertical If we make l small enough, then the electric field will be approximately
constant and radial throughout the cylindrical surface. There will be no flux through
the circular caps of the Gaussian cylinder if the field is radial, so the flux is only through
the [2 π l (.75 R)] surface area. The total volume of the rod is πR2 L and the volume of
the Gaussian cylinder is π(.75 R)2 l. This means that the charge inside the Gaussian
surface is qinside = Q [π(3/4 R)2 l / πR2 L] = Q [9l / 16L]. Gauss’ Law here says the
following: E A= qinside / ε0. Solve for E and plug in what qinside and A are:
E = (3 Q) / ( 8 π ε0 R L).
(b) How would you convince someone that the expression you got above
makes sense? - Make sure that your expression is consistent with causal dependencies
among the variables.
Here’s the Electric field at point A: E = (3 Q) / ( 8 π ε0 R L).
The units are right, since [k]=[1/ε0], so [E] = [k][charge]/[distance2], so that’s good,
but that doesn’t convince me yet.
What if I increase the charge Q on the rod? Then the electric field at point A
should increase also since now there’s more charge, so that matches my expression (By
the expression if Q increases, E increases - same as the physical/causal reasoning).
What if I increase the radius R of the rod? My expression says that the electric
field would decrease. Does that make sense? Well, if the radius increases, then the
charge on the rod is spread out more. The same net amount of charge will be exerting
an electric field at point A, but the charge will be farther away from that point, so the
electric field should be weaker. Alternatively, one could argue that increasing R, implies
that the charge is more spread out, and so less total charge is contained in the Gaussian
cylinder and so the field at A should be less.
What if the length L of the rod increases? Increasing the length also dilutes the
charge density. So again, less of the charge within the earlier Gaussian surface exerts a
field at A. This means that the electric field at point A should be less, as the expression
shows. Alternatively, if the charge is spread out (longer L), then less bits of charge are
close to A, and so the field at A decreases. And that is precisely what the math is saying
(L is in the denominator, and so increasing L, decreases E)
So the mathematical expression I got matches up with my physical sense of how
the electric field will change if I change one aspect of the situation.
6. A solid, spherical metal ball of radius R (black) and net charge +Q0 is fixed
at the center of a spherical shell of inner radius 3R, outer radius 4R, and charge –
5Q0 (grey).
(a) Find the electric field at a point a distance 2R from the center of the ball (Note:
Point is located in between the ball and the shell).
We can use Gauss’ Law to find the E-field at a point 2R from the center of the
ball. We choose a spherical Gaussian surface that has a radius of 2R, because
then we can use Gauss’ Law to reason about the E-field at a point on that surface.
We know that the E-field is the same everywhere on that surface, so we can take
it out of the integral. So, we just have to integrate over dA, which just gives us
the total area of the spherical Gaussian surface, which is 4π(2R)2. Also, we know
that qenclosed is just the charge on the smaller sphere, +Q0.
So, putting all of this together, Gauss’ Law becomes:
Rearranging this equation, we can find the electric field at this point:
Note that this is the same result that you would get using Coulomb’s Law for a
point charge. (Remember, k = 1/4πε0). In other words, the central sphere acts as a
point charge for this case, and the shell contributes a net zero to the field at A!
(d) What’s the electric field at a point inside the shell, a distance (3.5)R from the
center of the ball? Explain.
The total field inside a conductor, we know, is always zero. That is If the electric
field were not zero, then the unbound electrons inside the metal would
experience a force due to that field, and so would move—meaning that the
system would not be in equilibrium. When would they stop moving? Only after
they had distributed themselves so as to make the total field zero, at which point
no force acts on them. The system would then be in equilibrium.
(e)Find the total charge on the inner surface of the shell (at 3R). (ii) Find the total
charge on the outer surface of the shell (at 4R).
Now, we can use Gauss’ Law. We choose a spherical Gaussian surface that has a
radius of 3.5R. We know the field everywhere on this surface is zero (since it is
inside the metal shell)
So the total flux through that surface is zero.
By Gauss’s Law this means that the total charge enclosed by the surface must
also be zero.
Since the central ball has a charge of +Q, this implies that the inner surface of the
shell must have a charge of -Q so that the total charge enclosed by the Gaussian
sphere of radius 3.5R turns out to be zero.
Finally, this means that the remaining charge of the shell must be on the outer
surface, i.e., the outer surface would carry the charge of -4Q. (Again, none of this
charge can be in the body of the metal shell; by Gauss’s Law since the field
everywhere inside the metal is zero).