Download chapter 2((probability theory ))

chapter 2((probability theory ))
((1-2))count operation
1-(n factorial) is defined as the product of all the integers from 1 to n (the order of
multiplying does not matter) .we can use factorial to determine the number of
arrangement of n objects if we select n of them each time.
We write "n factorial" with an exclamation mark as follows: n!
n! = (n)(n − 1)(n − 2)...(3)(2)(1)
2-(permutation) An arrangement (or ordering) of a set of objects is called a
permutation. (We can also arrange just part of the set of objects.)In a permutation, the
order that we arrange the objects in is important
The number of permutations of n distinct objects taken r at a time, denoted by
Pnr,where repetitions are not allowed, is given by
3-(permutation with replication) An arrangement of selected (n) from (n) object but
with replication in the objects which it is given by:-
p=(n!)/(n1!.n2!…….nk!)
3-( A combination) of n objects taken r at a time is a selection which does not take
into account the arrangement of the objects. That is, the order is not important.
And given by
Note 1
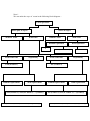
We can make the ways of count in the following block diagram :Count operation
Select part of object
Without order
Select all object
With order
Without order
Without replication
1
At the same time
Sequentially
Com (n taken r)
Without replacement
N!/(n1!.n2!...nk!)
At the same time
With order
With replication
N!
Sequentially
Per (n taken r)
With replacement
com (n taken 1). com (n-1 taken 1)…..((r times))
com (n taken 1). com (n-1 taken 1)…..((r times))
Without replacement
With replacement
Per (n taken 1). Per (n-1 taken 1)…..((r times))
Per (n taken 1). Per (n taken 1)…..((r times))
Note2- if we select (r) objects sequentially from (n) objects with replacement and the
order is important then we can find the count as :Per(n,1).per(n,1).per(n,1)….. ((r times )
Note3- if we select (r) objects sequentially from (n) objects without replacement and
the order is important then we can find the count as :Per(n,1).per(n-1,1).per(n-2,1)….. ((r times )
Note4- if we select (r) objects sequentially from (n) objects with replacement and the
order is not important then we can find the count as :comp(n,1).comp(n,1).comp(n,1)….. ((r times )
Note5- if we select (r) objects sequentially from (n) objects without replacement and
the order is not important then we can find the count as :comp(n,1).comp(n-1,1).comp(n-2,1)….. ((r times )
(2-2) The Binomial Theorem
We use the binomial theorem to help us expand binomials to any given power
without direct multiplication. As we have seen, multiplication can be time-consuming
or even not possible in some cases.
Properties of the Binomial Expansion (a + b)n


There are n + 1 terms.
The first term is an and the final term is bn.

Progressing from the first term to the last, the exponent of a decreases by 1
from term to term while the exponent of b increases by 1. In addition, the sum
of the exponents of a and b in each term is n.

If the coefficient of each term is multiplied by the exponent of a in that term,
and the product is divided by the number of that term, we obtain the
coefficient of the next term.
The binomial expansion (a+b)n can be written as
or
Note
The r th term of the expansion of
is:
(3-2)Pascal's Triangle
We note that the coefficients (the numbers in front of each term) follow a pattern.
[This was noticed long before Pascal, by the Chinese.]
1
11
121
1331
14641
1 5 10 10 5 1
1 6 15 20 15 6 1
Examples
1.
Expand
.
Let a = x, b = 2, n = 5 and substitute. (Do not
substitute a value for k.)
Find the 5th term of
.
Let r = 5, a = (3x), b = (-4), n = 12
and substitute.
(4-2) probability
1)) definitions
1-Any experiment whose outcome cannot be predicted in advance, but is one of the set of possible
outcomes, is called a random experiment.
2-A sample space is a set of all possible outcomes for an activity or experiment
Rolling a die
Tossing a coin
Drawing a card from a standard deck
Drawing one marble from the bottle
Rolling a pair of dice
12-
{1, 2, 3, 4, 5, 6}
{ Heads, Tails}
{52 cards}
{8 marbles}
{(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}
An event is the outcome or a combination of outcomes of an experiment. In other words, an
event is a subset of the sample space.
Probability If a trial results in n-exhaustive, mutually exclusive and equally likely cases and m
of them are favourable to the occurrence of an event A, then the probability of the happening of
A, denoted by P(A), is given by:
P(A) = m/n.
2)) properties of probability
We have the following properties of the probability function:
The previous properties represent formulas currently used in probability calculus on a finite field of
events.
Property (P9) is the main calculus formula for applications in finite cases.
In addition, if {Ω, Σ, P} is a σ-field, we also have the following properties:
Independent events. Conditional probability
Let us consider the experiment of tossing two coins and let A – heads on first coin and B – heads
on second coin be two events. The occurrence of event A and its probability do not depend on the
occurrence of event B, and vice versa. In this case, events A and B are said to be independent (each
isindependent of the other).
According to this definition, in the previous example we have: P(A and B) = P(A) x P(B) = (1/2) x
(1/2) = 1/4.
Consider an urn containing four white balls and three black balls. Two people extract one ball each
from the urn. Let A – first person is extracting a white ball and B – second person is extracting a white
ball be two events. The probability of event B, in the absence of information about A, is 4/7. If event A
has occurred, the probability of event B is 1/2, so event B depends on event A. Therefore, these two
events are not independent.
It is natural to call the probability of event B conditional on event A and to denote it by P(B│A).
Total probability formula. Bayes’s theorem
Bayes’s theorem is a main result in probability theory, which relates the conditional and marginal
probability of two aleatory events A and B. In some interpretations of probability, Bayes’s theorem
explains how to update or revise beliefs in light of new evidence.
Example:
In tossing a fair die, what is the probability that the outcome is odd or grater than 4?
Suggested answer:
Let E1 be the event that the outcomes are odd.
E1 = {1,3,5}
Let E2 be the event that the outcomes are greater than 4.
E2 = {5,6}
Example:
In tossing a die experiment, what is the probability of getting at least 2.
Suggested answer:
Let E be the event that the outcome is at least 2, then
E = {2,3,4,5,6}
EC= {1}
Below are some solved simple applications:
1) Find the probability of getting a multiple of 2 at a die roll.
Solution:
The number of outcomes that are favorable to respective event is three (these are: {2}, {4},
{6}). The number of equally possible outcomes is six, so the probability is 3/6 = 1/2 = 50%.
2) There are three pairs of socks of different colors in a basket. Two socks are randomly extracted
from the basket. What is the probability of getting two socks of same color?
Solution:
The number of equally possible cases is the number of all 2-size combinations of socks, namely,
C(6, 2) = 15. The number of favorable cases is three, because we have three pairs of socks having the
same color. Thus, the probability is 3/15 = 1/5 = 20%.
3) An urn contains four white balls and six black balls. Two balls are drawn simultaneously. Find
the probability of the events: a) A – drawing two white balls; b) B – drawing two black balls; c) C –
drawing two balls of the same color.
4) Two dice, one red and one blue, are rolled. Consider the events: A – occurrence of a number less
than 4 on the red die; B – occurrence of a number less than 3 on the blue die. Find
.
P(A or B)
Solution:
The cases that are favorable to A are {1}, {2} and {3}; therefore, P(A) = 3/6. The cases that are
favorable to B are {1} and {2}; therefore,P(A) = 2/6.
The cases that are favorable to A and B correspond to the ordered pairs (1, 1), (1, 2), (2, 1),
(2, 2), (3, 1), (3, 2), and total six, in a probability field where the number of equally possible cases is 6
x 6 = 36. We then have P(A and B) = 6/36. The requested probability is
5) At a blackjack game, calculate the probability for a player to get a total of twenty points from
the first two cards (provided no other cards are shown), if a 52-card deck is used.
Solution:
The variants totaling twenty points are of the type A + 9 or 10 + 10 (as a value; that is, any 2-size
combination of cards from 10, J, Q, K). We have sixteen variants A + 9 (4 aces and 4 nines) and C(16,
2) = 120 variants 10 + 10 (all 2-size combinations of cards from the sixteen cards with a value of 10).
The number of all possible distribution variants for two cards is C(52, 2)=1326 . The probability is then
P = (16 + 120)/1326 = 68/663.
6) We have two urns, the first containing three white balls and four black balls and the second
three white balls and five black balls. A ball is drawn from a randomly chosen urn. Find the probability
for the drawn ball to be white.
Solution:Denote the events: A – the first urn is the chosen one; B – the second urn is the chosen one;
C – the drawn ball is white. A and B form a complete system of events and P(A) = P(B) = 1/2.
We have P(C│A) = 3/7 and P(C│B) = 3/8. According to total probability formula, we have:
P(C) = P(A)P(C│A) +P(B)P(C│B) = (1/2) x (3/7) + (1/2) x (3/8) = 45/112 = 0.40178.
7) Five cards are drawn at once from a 32-card deck. What is the probability of the five cards
containing at least one queen (Q)?
Solution:
Denoting by A the event to be measured the five extracted cards contain at least one Q, we then
calculate the probability of the contrary event A – the five extracted cards contain no Q.
The equally possible elementary events are the occurrences of 5-size combinations of cards from the
32, a total of
. The combinations that are favorable to event A have the form (xyztv), with x,
C(32, 5)
y, z, t, v taking any card as value, except the four Q-cards. They total
.
C(32 - 4, 5) = C(28, 5)
We then have: