Download Work - gandell

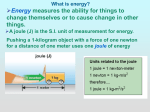
Work, Power, Energy
Work
Vocabulary
•
•
•
•
Work (force x distance)
Kinetic Energy ( ½ mass x velocity2)
Potential Energy( mass x g x height)
Review P = mv
J = mΔv
F = ma
The Daytona 500 ( centimeters that is!!!)
World’s Fastest Roller Coaster
•
•
•
•
How did the car get up high?
What changes take place during fall?
What changes take place during rise?
Are these changes related?
Work
• Work – Exerting force in a way that makes
a change in the world.
– Throwing a rock is work: you’re exerting a
force, and the rock’s location changes (i.e. “the
world has been changed”)
– Pushing on a brick wall is not work: you’re
exerting a force, but “the world doesn’t change”
(the wall’s position doesn’t change).
Work
• So exerting force alone isn’t enough. You have to
both exert a force, and make a change.
• If you’re not exerting a force, you’re not doing work.
• Example: Throwing a ball.
– While you are “throwing the ball” (as opposed to just
holding it) you are exerting a force on the ball. And the ball
is moving. So you’re doing work.
– After the ball leaves your hand, you are no longer exerting
force. The ball is still moving, but you’re no longer doing
work.
Work Done By “Lifting” Something
• When we were pushing something along the ground,
the work done didn’t depend on the mass.
• Lifting up something does do work that depends on
mass.
• Because of gravity:
– Gravity always pulls down with a force equal to mg,
where m is the mass, and g = 9.8 m/s2.
– So we must exert at least that much force to lift
something.
– The more mass something has, the more work required to
lift it.
W = Fd cos
• The work done by force is defined as the product of
that force times the parallel distance over which it
acts.
• The unit of work is the newton-meter, called a joule
(J)
• The kilowatt hour is the unit of work. If a force is
doing work at a rate of 1 kilowatt (which is 1000J/s),
then in 1 hour it will do 1kW.h of work.
A kW.h = 3.6 x 106 J
• Work is a scalar
Force is NOT Work
If the force is perpendicular to the
direction the object moves, the work
done is 0.
If the object doesn’t move, the work
done is 0.
Two Conditions for Work
• 1. Force must act through a distance
• 2. Distance must be in the direction of force
• Discuss work required for satellite orbit
Negative Work
• All of our examples have increased the
potential energy or the kinetic energy
• Recall,
Work = (Force in the direction of motion) x
distance traveled in the direction of the force
• When force is opposite the direction of
motion, negative work is done.
– Work decreases the energy
Working at an advantage
Often we’re limited by the amount of force we can
apply.
Simple Machines such as ramps, levers, pulleys, etc
allow us to do the same amount of work, but by
applying a smaller force over a larger distance
Work = Force x
=
Force
x
Distance
Distance
Ramps
Ramps allow the exertion of a smaller force
over a longer distance to achieve the same
change in gravitational potential energy (the
same amount of work)
M
Horizontal Force and the Resulting
Horizontal Acceleration
• Only the horizontal
component of the
force does work in the
horizontal
• How much work is
done moving the
wagon 3 meters?
Vertical Work???
• I lift a book of mass 2 kg. from the floor to
the desk, or 1.2 meters. W = ???
• I lift the same book from the desk to 2.2 m
above the desk. W = ???
• What work is done to get the same book
from the floor to total height of 3.3m ??
Work, Power, Energy
Power
Power
Rate of doing work:
Power = Work per unit time
(1 Joule per second = 1 Watt)
1000 Watts = 1 kilowatt
1 horsepower (hp) = 746 W
Power is a scalar quantity
Power
The rate of using energy
If you do 100 joules of work in one second
(using 100 joules of energy), the power is
100 watts
Power keeps something moving:
W Fd
P

Fv
t
t
Work, Power, Energy
Work-Energy Theorem
Work – Energy Theorem
The work done on an object by a net force
equals the object’s change in kinetic energy.
Wnet = DKE
The amount of energy transferred to the object
is equal to the work done. DE = W
In changing speed from 0 to v, work is done.
The kinetic energy increases by an amount
equal to the work done.
Energy
The capacity to do work.
You must have energy to accomplish work –
it is like the "currency" for performing work.
To do 100 joules of work, you must expend 100
joules of energy.
Doing work exchanges energy
• Kinetic Energy = energy of motion
– A rolling bowling ball can “do work”
– A falling anvil can do work
• Potential Energy = Latent capacity for doing work
– Gravitational potential energy
– Nuclear potential energy
– Chemical potential energy
• Processes can convert energy from one form to
another, but the total amount is always conserved.
• Why is the usable energy decreasing even though
total energy is conserved??
Energy
• We call this “energy of motion” kinetic
energy.
• An object’s kinetic energy is given by this
equation:
K = ½ mv2
Velocity of the moving object
(m/s)
Mass of the moving object (kg)
Kinetic Energy (J)
Remember the Book?
• If we put work into the book to lift it, where
did that work energy go???
• Can we get it back??
Potential Energy (stored energy)
• Potential Energy – The amount of energy
something has “available” that can be
converted to other forms of energy.
• There are different “sources” of potential
energy.
• Gravity – Gravity can exert force through a
distance.
– Force – force due to gravity between the two
objects.
– Distance – how far an object is allowed to fall.
Energy can be converted into other forms
• As something falls, gravitational potential
energy is converted into kinetic energy
• A sliding frictional force converts kinetic
energy into “thermal energy”
– Just rub your hands together!
– Where did that energy originate?
• If you “do work” on something, you change
its energy by an amount equal to the work
done.
Work, Power, Energy
Kinetic Energy
+
Potential Energy
=
Mechanical Energy
Kinetic Energy
• The energy possessed by an object because
it is in motion.
• Is a scalar quantity
• Units of kinetic energy: Joules
• An object with mass of 1 kg, moving at 1
m/s, has a kinetic energy of 0.5 Joule.
KE  mv
1
2
2
Kinetic Energy
An object’s kinetic energy depends on:
the object’s mass.
Kinetic energy is directly proportional to
mass.
the object’s speed.
Kinetic energy is directly proportional to the
square of the object’s speed.
Destructive energy is proportional to KE!
PE - Mechanical
Potential Energy
• Work is not always converted directly into
kinetic energy. Instead it is “stored”, or
“hidden”.
• Potential energy is stored energy or stored
work.
• Potential energy is energy that an object
(system) has due to its position or
arrangement.
PE = - WorkF
Gravitational Potential Energy
• is the energy possessed by an object because of a
gravitational interaction.
• The gravitational potential energy of an object at
height h equals the negative of the work that gravity
does when the object is lifted from the PE = 0
position
PEg = mgh (= W x h or
F x h or F x dist.)
Elastic Potential Energy
• A spring or other elastic media can store potential
energy
• Can define PE as the work required by a external
force to move the object without acceleration
between the two points
• As spring is stretched (or compressed) the force
changes, so we must average.
1 2
PE elastic  k x
2
Work, Power, Energy
Conservation of Energy
Mechanical Energy
• Mechanical Energy = PE + KE
• Energy by itself is impossible to determine
(you can’t measure energy of any object at
any single state) but you can measure
changes in energy.
Conservation of Energy
• The Law of Conservation of Energy states that
within a closed, isolated system, energy can
change form, but the total amount of energy is
constant. Energy can neither be created nor
destroyed.
• If no external forces act on a system, the
total energy of the system will remain
constant.
(KE  PE)inital  W  (KE  PE)final
Conservation of Energy
As you throw a ball up in the air, the moment it leaves
your hand the ball has little potential energy but a lot of
kinetic energy.
As the ball moves upward, the kinetic energy is
transferred to potential energy and the ball slows down.
At the top of the path, the ball has stopped traveling
upward and has transferred all the kinetic energy into
potential energy.
Because of the force due to gravity, the ball starts to
move down, the potential energy converting to kinetic
energy, increasing the velocity of the ball, until it is
caught.
KE-PE on an Inclined Plane
KE-PE in a Pendulum