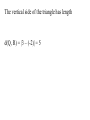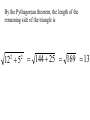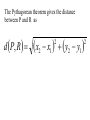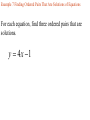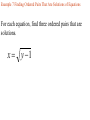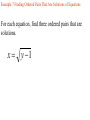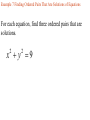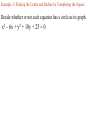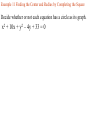* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 2.1 Powerpoint
Survey
Document related concepts
Transcript
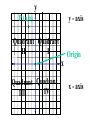
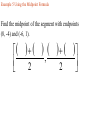
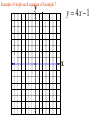
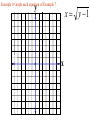
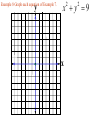
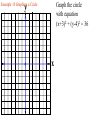
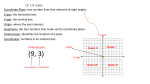
Chapter 2.1 Graphs of Equations The idea of pairing one quantity with another is often encountered in everyday life. For example, a numerical grade in a mathematics course is paired with a corresponding letter grade. the number of gallons of gasoline pumped into a tank is paired with the amount of money needed to purchase it. Another example is shown in the table, which gives the dollars the average American spent in 2001 on entertainment. For each type of entertainment, there is a corresponding number of dollars spent. Pairs of related quantities, such as a 96 determining a grade of A, 3 gallons of gasoline costing $5.25, and 2001 spending on CDs of $47, can be expressed as ordered pairs: (96, A), (3, $5.25), (CDs, $47). An ordered pair consists of two components, written inside parentheses, in which the order of the components is important. Example 1 Writing Ordered Pairs Use the table to write ordered pairs to express the relationship between each type of entertainment and the amount of money spent on it. (a) DVD rentals/sales Example 1 Writing Ordered Pairs Use the table to write ordered pairs to express the relationship between each type of entertainment and the amount of money spent on it. (b) movie tickets In mathematics, we are most often interested in ordered pairs whose components are numbers. Note that (4,2) and (2,4) are different ordered pairs because the order of the numbers is different. The Rectangular Coordinate System. As mentioned in Chapter R, each real number corresponds to a point n a number line. This idea is extended to ordered pairs of real numbers by using tow perpendicular number lines, one horizontal and one vertical, that intersect at their zero-points. This point of intersection is called the origin. The horizontal line is called the x-axis, and the vertical line is called the y-axis. Starting at the origin, on the x-axis the positive numbers go to the right and the negative numbers go to the left. The y-axis has positive numbers going up and the negative numbers going down. The x-axis and y-axis together make up a rectangular coordinate system, or Cartesian coordinate system (names for one of its coinventors, Rene Descartes; the other coinvertor was Pierre de Fermat). The plane into which the coordinate system is introduced is the coordinate plane, or xy-plane. The x-axis and y-axis divide the plane into four regions, or quadrants, labeled as shown in Figure 1. The points on the x-axis and y-axis belong to no quadrant. y P (a,b) y - axis Quadrant Quadrant II I Origin x Quadrant Quadrant IV III x - axis Each point P in the xy-plane corresponds to a unique ordered pair (a,b) of real numbers. The numbers a and b are the coordinates of point P. To locate on the xy-plane the point corresponding to the ordered pair (3,4), for example, start at the origin, move 3 units in the positive x-direction, and then move 4 units in the positive y-direction. Point A corresponds to the ordered pair (3,4). Also in figure 2, B corresponds to the ordered pair (-5,6), C to (-2, -4), d TO (4,3), and E to (-3,0). The point P corresponding to the ordered pair (a,b) often is written P(a,b) as in Figure 1 and referred tp as “the point (a,b).” The Distance Formula Recall that the distance on a number line between the points P and Q with coordinates x1 and x2 is d(P,q) = |x2 – x1| = |x1 – x2| By using the coordinates of their ordered pairs, we can extend this idea to find this distance between any two points in a plane. Figure 3 shows the points P(-4, 3) and R(8, -2) To find the distance between these points we complete a right triangle as in the figure. This right triangle has its 900 angel at Q(8, 3). The horizontal side of the triangle has length d(P, Q) = |8 – (-4)| = 12 The vertical side of the triangle has length d(Q, R) = |3 – (-2)| = 5 By the Pythagorean theorem, the length of the remaining side of the triangle is 12 5 2 2 144 25 169 13 This the distance between (-4, 3) and (8, -2) is 13 To obtain a general formula for the distance between two points in a coordinate plane, let P(x1, y1) and R (x2, y2) be any two distinct points in a plane, as shown in Figure 3. Complete a triangle by locating point Q with coordinates (x2, y1). d P, R x2 x1 y2 y1 2 2 The Pythagorean theorem gives the distance between P and R as d P, R x2 x1 y2 y1 2 2 Distance Formula Suppose that P(x1, y1) and R (x2, y2) are two points in a coordinate plane. The distance between P and R, written d(P, R) is given by the distance formula, d P, R x2 x1 y2 y1 2 2 Example 2 Using the Distance Formula Find the distance between P(-8, 4) and Q(3, -2) Example 3 Determine Whether Three Points Are the Vertices of a Right Triangle Are points M(-2, 5), N(12, 3) and Q(10, -11) the vertices of a right triangle? d M , N d M , Q d N , Q 2 2 2 2 2 2 Example 4 Determine Whether Three Points Are Colllinear Are points M(-1, 5), N(2, -4) and Q(4, -10) collinear? d M , N d M , Q d N , Q 2 2 2 2 2 2 Midpoint Formula The midpoint of the line segment with endpoints (x1, y1) and (x2, y2) is x1 x2 y1 y2 , 2 2 Example 5 Using the Midpoint Formula Find the midpoint of the segment with endpoints (8, -4) and (-6, 1). , 2 2 Example 6 Applying the Midpoint Formula to Data Figure 8 depicts how the number of McDonald restaurants worldwide increased from 1995 to 2001. Use the midpoint formula and the two given points to estimate the number of restaurants in 1998, and compare it to the actual (rounded) figure of 24,000. 2 , 2 Example 6 Applying the Midpoint Formula to Data Figure 8 depicts how the number of McDonald restaurants worldwide increased from 1995 to 2001. Use the midpoint formula and the two given points to estimate the number of restaurants in 1998, and compare it to the actual (rounded) figure of 24,000. 1995 2001 18000 30000 , 2 2 Example 7 Finding Ordered Pairs That Are Solutions of Equations For each equation, find three ordered pairs that are solutions. y 4x 1 Example 7 Finding Ordered Pairs That Are Solutions of Equations For each equation, find three ordered pairs that are solutions. x y 1 Example 7 Finding Ordered Pairs That Are Solutions of Equations For each equation, find three ordered pairs that are solutions. x y 1 Example 7 Finding Ordered Pairs That Are Solutions of Equations For each equation, find three ordered pairs that are solutions. x y 9 2 2 Example 8 Graph each equation of Example 7. y y 4x 1 x Example 8 Graph each equation of Example 7. y x y 1 x Example 8 Graph each equation of Example 7. y x y 9 2 x 2 Example 9 Finding the Equation of a Circle Find and equation for the circle having radius 6 and center at (-3, -4) 6 x y 2 2 Center-Radius Form of the Equation of a Circle The circle with center (h, k) and radius r has the equation x h y k 2 2 r 2 The center-radius form of the equation of a circle. A circle with center (0, 0) and radius r has equation 2 2 2 x y r Example 10 Graphing a Circle Graph the circle with equation (x+3)2 + (y-4)2 = 36 y x Example 11 Finding the Center and Radius by Completing the Square Decide whether or not each equation has a circle as its graph. x2 – 6x + y2 + 10y + 25 = 0 Example 11 Finding the Center and Radius by Completing the Square Decide whether or not each equation has a circle as its graph. x2 + 10x + y2 – 4y + 33 = 0 Example 11 Finding the Center and Radius by Completing the Square Decide whether or not each equation has a circle as its graph. 2x2 + 2y2– 6x + 10y = 1 Homework Section 2.1 # 1 - 64