* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Survey
Document related concepts
Transcript
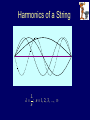
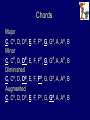
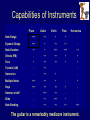
Physics, Mathematics, Music and Perhaps a Bit of Biology Steven A. Jones This Presentation Draws From 1. 2. 3. 4. General Engineering Background One year graduate sequence in acoustics Twenty nine years of playing guitar 19 Years of Research in Medical Ultrasound Stuff I Didn’t Know 1. Where the notes are on the guitar (vs piano). 2. Importance of rhythm 1. Triples 2. 5-tuples 3. Other African animals 3. 4. 5. 6. 7. What is interpretation? Concept of Voices Cerebellar Function How keys work How chords work More Stuff I Didn’t Know 8. Harmonic Analysis 9. What tone is 10. Rubato 11. Dynamics 12. Major/Minor 3rd/5th etc. 13. Major/Minor Scales Vibration of a String The wave equation 2 2 y y 2 c 2 t x 2 T c • Behavior in time is the same as behavior in space • Wave Speed depends on tension (T) and string density per unit length ( ) t1 y x t2 General Solution to the Equations y( x, t ) f (ct x) g ct x Meaning: The string shape can propagate along the string in the forward and/or reverse direction. Initially Stationary String If the string is not moving initially, must have: v 0 y ( x, t ) 0 cf ( x ) cg x 0 t t 0 f ( x) g x -x 0 +x Forward and reverse waves are inverted copies (except for constant). Boundary Conditions Boundary Conditions Initial Conditions y (0, t ) 0 y ( L, t ) 0 y ( x,0) f ( x ) y ( x,0) v( x ) t Plucked String Struck String Boundary Conditions Constrain Allowable Frequencies Assume simple harmonic motion: y( x, t ) A1ei t kx A2 ei t kx y(0, t ) 0 A1eit A2 eit 0 A2 A1 y x, t Aeit e ikx e ikx 2iA sin kxe it Re 2 sin kx Ar sin t Ai cost 2nc y L, t 0 ; n 1, 2, 3, ..., L Harmonics of a String L ; n 1, 2, 3, ..., n String Shapes/Vibration Modes – 1st Harmonic is a Sine Wave – 2nd Harmonic is 2x the frequency of the 1st – Since the middle of the string doesn’t move for 2nd harmonic, can touch it there & still get vibration. – 3rd harmonic has two nodes (at 1/3 and 2/3rds the string length) – The “harmonics” give pure tones. – Can do harmonics with fretted strings. Color Fourier Interpretation: Tone depends on the relative loudness & phases of each harmonic. The Frequencies (Musician’s Terminology) • • • • • • • C, C#, D, D#, E, F, F#, G, G#, A, A#, B Do Re Mi Fa Sol La Ti Major 3rd (C to E) Major 5th (C to G) Minor 3rd (C to D#) Major/Minor 7th (C to A# / B) Barbershop Quartet (C, E, G, Bb) The Frequencies (Musician’s Terminology) C, C#, D, D#, E, F, F#, G, G#, A, A#, B Do Re Mi Fa Sol La Ti Why are there no sharps (black keys) between E&F and B&C? Chords Major C, C#, D, D#, E, F, F#, G, G#, A, A#, B Minor C, C#, D, D#, E, F, F#, G, G#, A, A#, B Diminished C, C#, D, D#, E, F, F#, G, G#, A, A#, B Augmented C, C#, D, D#, E, F, F#, G, G#, A, A#, B Chords Diminished Seventh C, C#, D, D#, E, F, F#, G, G#, A, A#, B Note that C7dim is the same as D#7dim, F#7dim and A7dim. This is an ambiguous chord and can resolve into many possible chords. There are only 4 diminished 7th chords. Frequencies Used in Music Frets on a Guitar • Each fret shortens the string by the same percentage (r) of it’s current length. • Frets must get closer together. • Takes 12 frets to get to ½ the length. 1 12 12 • Must have r 1 2 r 1 2 • Thus, r = 0.943874313 • Or 1/r = 1.059463094 Postulates Tones separated by nice fractional relationships are pleasing. Tones separated by complicated fractional relationships are less pleasing. These postulates are the basis of “Just Intonation” (Slogan: “It’s not just intonation, its Just intonation!”) Pythagorean Scale • Pythagorus proposed the scale cdefgab, based on a series of “perfect 5ths” • c=1 • g = cx3/2 (i.e. 1 ½) • d = (gx3/2)/2 = c x (9/4)/2 (i.e. 1 1/8) • a = (dx3/2) = c x (27/16) (i.e. 1 11/16) Circulate through c-g-d-a-e-b-f-c But note that the second “c” doesn’t work. It’s 37 2187 11 1.0679 2 2048 Values of Frequencies N Ratio Note 0 1 2 3 4 5 6 7 8 9 10 11 12 1.0000 1.0595 1.1225 1.1892 1.2599 1.3348 1.4142 1.4983 1.5874 1.6818 1.7818 1.8877 2.0000 C C# D D# E F F# G G# A A# B C Approximation 1 1 1/16 1 1 /8 1¼ 1 1/3 1 3/8? (=1.375) 1½ 1 5/8? (=1.625) 1 2 /3 1¾ 1 7/8 (=1.875) Pythagorean 1 1 /8 1.266 1 1/3 1½ 1.687 1.898 Harmonics of a String N Octave N/O Note 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 2 4 4 4 4 8 8 8 8 8 8 C C G * C E * G Bb * C D E F# (ish) B G# (ish) 1 1 1½ 1 1¼ 1.5 1¾ 1 1 1 /8 1¼ 1 3 /8 1½ 1 5 /8 When you play a C, you are also playing G, E, Bb, etc. in different amounts and in Just Intonation. Harmonics • Were not invented by Yes or Emerson, Lake and Palmer. • Can be combined with natural tones. – Granados Historical Notes • 12 tone system (Even Tempered Scale) relatively recent invention (ca. 1700s). • Bach used “Well Tempered Scale” • We don’t hear Toccata & Fugue the way it was written. Why 12 Notes? • Even temperament would not work as well with other spacings (besides 1/12) • Works pretty well with a spacing of 17. – Other countries use a 17 tone system. – Google: “17 tone” music 0 1.0000 C 1 1.0416 2 1.0850 3 1.1301 D 1.1225 4 1.1771 D# 1.1875 5 1.2261 6 1.2772 E 1.25 7 1.3303 F 1.333 8 1.3857 F# 1.375 9 1.4433 10 1.5034 G 1.5 11 1.5660 12 1.6311 G# 1.625 13 1.6990 A 1.667 14 1.7697 A# 1.75 15 1.8434 B 1.875 16 1.9201 17 2.0000 17 Tone Scale Color • Determined by the weights of the higher harmonics. • Musette …. – Bach denotes the “crisper” sound as “metallic.” – What is “metallic?” Vibrating Bar • Equation • Boundary Conditions • Harmonics – Not integer multiples – Sound speed depends on frequency – A cacaphony of sounds – Nodes – Damping Vibrating Bar • Equation 2 y 2E 4 y 2 t x 4 • Boundary Conditions radius of gyration – Clamped • Displacement = 0 (y) • Slope = 0 (1st derivative wrt x) – Free • Bending Moment = 0 • Shear Force = 0 (2nd derivative wrt x) (3rd derivative wrt x) Vibrating Bar • Allowed Frequencies Are Roots of: cosh2l cos2l 1 1 0.597 2l ; 2 1.494 2l ; 3 2.5 2l ; etc. These are not integer multiples of one another. Sound is different from Bach’s “Metallic” Vibrating Bar A tuning fork is a bent vibrating free-free bar held at the center node. • Higher Modes Damp Out Quickly • 1st mode provides a pure tone. Tuning Fork • When you strike a tuning fork, at first the tone sounds harsh, but then it’s very very pure.1 1 With apologies to James Joyce. Fourier View Breakdown Notes are finite in time. Stopping Strings Damping Notes are not discrete frequencies – they are broadened. Breakdown of the Fourier View (Goodbye Fourier Series, Hello Fourier Transform) A# A# (smeared) Neurophysiology • It is hard to imagine being able to make the complicated movements of playing a musical instrument. • Much of music is performed by the cerebellum • Purkinje cells adapt and change as we learn. • Practice from different starting points. Capabilities of Instruments Piano Guitar Violin Flute Harmonica Note Range +++ ++ + + - Dynamic Range +++ + ++ ++ - Note Duration ++ + +++ +++ ++ Vibrato (FM) - ++ ++ + + Tone + ++ ++ + + Tremolo (AM) - ++ Harmonics - ++ + Multiple Notes +++ ++ + - + Keys +++ ++ ++ + - Hammer-on/off - +++ ++ - - Slide - ++ +++ + - Note Bending - ++ ++ ++ +++ - The guitar is a remarkably mediocre instrument. Dissonance Major Chord (e.g. C E G) is Pleasant. It is the unpleasant sounds that give the most pleasure. • It feels good when it stops hurting. • In the context of the familiar, the unfamiliar holds the most interest. – Example: Bach’s Prelude in Dm To Add • • • • • • • Resolution Rhythm Rubato Dynamics Amplitude Modulation Fingernails Chords (Major, Minor, Inversion, 3rd, 5th, Diminished, Augmented).