Download 6-5 Trapezoids and Kites

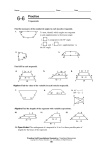
6-5 TRAPEZOIDS AND KITES (p. 320-325)
Let’s review some terminology that is associated with trapezoids.
Example: Sketch a trapezoid and identity the following sides and angles.
C
D
A
B
The bases of a trapezoid are the parallel sides, while the legs are the nonparallel sides. In
an isosceles trapezoid, the legs are congruent.
A trapezoid has two pairs of base angles, sometimes referred to as the upper base angles
and lower base angles. Each pair of base angles includes a base of the trapezoid.
Theorem 6-15
The base angles of an isosceles trapezoid are congruent.
You will follow a plan in homework problem #26 and prove this theorem.
How do the angles that share or include a leg in a trapezoid compare to each other?
Which theorem helps you reach this conclusion?
Since certain angle pairs in a trapezoid are congruent and other angle pairs are
supplementary, there are good algebra problems involving the angles of a trapezoid.
Example: XYZW is an isosceles trapezoid. Also, m X  3x  24 and m W  2x - 14.
Find m Y, m Z, and m W by setting up and solving an equation.
X
W
Y
Z
Do 1 on p. 321.
Theorem 6-16
The diagonals of an isosceles trapezoid are congruent.
Theorem 6-16 is an easy theorem to prove. To prove it, use congruent triangles.
Students can do this during their presentations.
Example: In isosceles trapezoid RSTU, RT  2x  14 and SU  8x - 42. Find RT by
setting up and solving an equation.
R
S
U
T
The diagonals of a kite are not always congruent. However, these diagonals do have a
relationship to each other.
Theorem 6-17
The diagonals of a kite are perpendicular.
Theorem 6-17 can be proved without using congruent triangles. You can use the theorem
that says if a point is equidistant from the endpoints of a segment, then it is on the
perpendicular bisector of the segment. (Short form: Equidistant pt.  pt. on  bis.).
Example:
B
A
C
D
In kite ABCD, AB  AD. Thus, which point is equidistant from B and D?
What other two sides of the kite are congruent? Thus, name a second point that is
equidistant from B and D.
What special line is AC with respect to BD ?
Example:
K
2
J
3
67
1
D
L
M
In kite JKLM, JK  JM and KL  LM. By what method(s) is JKD  JMD?
If m JMD  67, find m 1, m 2, and m 3.
Do 3 on p. 322.
Homework p. 322-325: 5,7,11,13,17,18,22,24,26,27,30,31,34,45-49,51-53
18. Solve 2x  2(2x - 3)  66.
27. Solve x  6  2x  90.
34. Yes, if two congruent angles are right angles. The other two angles are also
supplementary.