Download ppt - UNT Mathematics

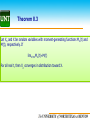
Chapter 8. Some Approximations to
Probability Distributions: Limit Theorems
Sections 8.2 -- 8.3: Convergence in Probability
and in Distribution
Jiaping Wang
Department of Mathematical Science
04/22/2013, Monday
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Outline
Convergence in Probability
Convergence in Distribution
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Part 1. Convergence in Probability
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Introduction
Suppose that a coin has probability p, with 0≤p≤1, of coming up
heads on a single flip. Suppose that we flip the coin n times,
what can we say about the fraction of heads observed in the n
flips?
For example, if p=0.5, we draw different numbers of trials in a
simulation, the result is given in the table
n
100
200
300
400
%
0.4700
0.5200
0.4833
0.5050
0.02
0.0167
0.005
|%-0.5| 0.03
From here, we can find when n∞, the ratio is closer to 0.5
and thus the difference is closer to zero.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Definition 8.1
In mathematical notations, let X denote the number of heads
observed in the n tosses. Then E(X)=np, V(X)=np(1-p). One
way to measure the closeness of X/n to p is to ascertain the
𝑋
probability that the distance |
− 𝑝| will be less than a pre𝑛
assigned small value ε so that 𝑃
𝑋
𝑛
− 𝑝 < 𝜀 → 1.
Definition 8.1: The sequence of random variables X1,X2, .., Xn
is said to convergence in probability to the constant c, if for
every positive number ε,
lim 𝑃 𝑋𝑛 − 𝑐 < 𝜖 = 1 .
𝑛→∞
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Theorem 8.1
Weak Law of Large Numbers: Let X1,X2, .., Xnbe independent
and identical distributed random variables, with E(Xi)=μ and
1 𝑛
2
V(Xi)=σ <∞ for each i=1,…, n. Let 𝑋𝑛 =
𝑋 . Then, for any
n 𝑖=1 𝑖
positive real number ε,
lim 𝑃 𝑋𝑛 − 𝜇 ≥ 𝜀 = 0
Or
𝑛→∞
lim 𝑃 𝑋𝑛 − 𝜇 < 𝜀 = 1.
𝑛→∞
Thus, 𝑋𝑛 converges in probability toward μ.
The proof can be shown based on the Tchebysheff’s theorem with
𝜀
2
2
X replaced by 𝑋𝑛and σ by σ /n, then let 𝑘 =
𝑛.
𝜎
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Theorem 8.2
Suppose that Xn converges in probability toward μ1 and Yn
converges in probability toward μ2. Then the following statements
are also true.
1. Xn+Yn converges in probability toward u1+u2.
2. XnYnconverges in probability toward u1u2.
3. Xn/Yn converges in probability toward u1/u2, provided u2≠0.
4. Xn converges in probability toward u1, provided P(Xn≥0)=1.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Example 8.1
Let X be a binomial random variable with probability of success p and number
of trials n. Show that X/n converges in probability toward p.
Answer: We have seen that we can write X as ∑Yi with Yi=1 if the i-th trial results in
Success, and Yi=0 otherwise. Then X/n=1/n ∑Yi . Also E(Yi)=p and V(Yi)=p(1-p).
Then the conditions of Theorem 8.1 are fulfilled with μ=p and σ2=p(1-p)< ∞ and thus
we can conclude that, for any positive ε,
limn∞P(|X/n-p| ≥ε)=0.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Example 8.2
Suppose that X1, X2, …, Xn are independent and identically distributed random
Variables with 𝐸(𝑋𝑖) = 𝜇1, 𝐸(𝑋𝑖2) = 𝜇2, 𝐸(𝑋𝑖3) = 𝜇3, 𝐸(𝑋𝑖4) = 𝜇4 and all assumed
finite. Let S2 denote the sample variance given by
1
𝑆2 =
𝑋𝑖 − 𝑋 2.
𝑛
2
Show that S converges in probability to V(Xi).
Answer: Notice that 𝑆2 =
1
1
𝑛
𝑛
2
2
𝑖=1 𝑋𝑖 − 𝑋
where 𝑋 =
1
𝑛
𝑛
𝑖=1 𝑋𝑖 .
The quantity 𝑛 𝑛𝑖=1 𝑋𝑖2 is the average of n independent and identical distributed
variables of the form 𝑋𝑖2 with E(𝑋𝑖2 )= 𝜇2, and V (𝑋𝑖2 )= 𝜇4 - 𝜇22, which is finite. Thus
1
Theorem 8.1 tell us that 𝑛 𝑛𝑖=1 𝑋𝑖2 converges to 𝜇2 in probability. Finally, based on
1
Theorem 8.2, we can have 𝑆2 = 𝑛 𝑛𝑖=1 𝑋𝑖2 − 𝑋2 converges in probability to 𝜇2 - 𝜇12
=V(Xi).
This example shows that for large samples, the sample variance has a high
probability of being close to the population variance.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Part 2. Convergence in Distribution
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Definition 8.2
In the last section, we only study the convergence of certain random variables
Toward constants. In this section, we study the probability distributions of
certain type random variables as n tends toward infinity.
Definition 8.2: Let Xn be a random variable with distribution function Fn(x). Let
X be a random variable with distribution function F(x). If
limn∞Fn(x)=F(x)
At every point x for which F(x) is continuous, then Xn is said to converge in
distribution toward X. F(x) is called the limiting distribution function of Xn.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Example 8.3
Let X1, X2, …, Xn be independent uniform random variables over the interval (θ,
0) for a negative constant θ. In addition, let Yn=min(X1, X2, …, Xn). Find the
limiting distribution of Yn.
Answer: The distribution function for the uniform random variable Xi is
0, 𝑥 < 𝜃
𝐹(𝑋𝑖) = 𝑃(𝑋𝑖 ≤ 𝑥) =
𝑥−𝜃
,
−𝜃
𝜃≤𝑥≤0
1, 𝑥 > 0.
We know 𝐺 𝑦 = 𝑃 𝑌𝑛 ≤ 𝑦 = 1 − 𝑃 𝑌𝑛 > 𝑦 = 1 − 𝑃 min 𝑋1, 𝑋2, … , 𝑋𝑛 > 𝑦
= 1 − 𝑃 𝑋1 > 𝑦 𝑃 𝑋2 > 𝑦 … 𝑃 𝑋𝑛 > 𝑦 = 1 − 1 − 𝐹𝑋 𝑦 𝑛
0, 𝑦 < 0
0, 𝑦 < 0
= 1−
𝑦 𝑛
,
𝜃
𝜃 ≤ 𝑦 ≤ 0 so we can find lim 𝐺(𝑦) =
1, 𝑦 > 0.
0, 𝑦 < 𝜃
=
1, 𝑦 ≥ 𝜃.
𝑛→∞
lim 1 −
𝑛→∞
𝑦 𝑛
,
𝜃
𝜃≤𝑦≤0
1, 𝑦 > 0.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Theorem 8.3
Let Xn and X be random variables with moment-generating functions Mn(t) and
M(t), respectively. If
limn∞Mn(t)=M(t)
For all real t, then Xn converges in distribution toward X.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Example 8.4
Let Xn be a binomial random variable with n trials and probability p of success
on each trial. If n tends toward infinity and p tends zero with np remaining
fixed. Show that Xn converges in distribution toward a Poisson random variable.
Answer: We know the moment-generating function for the binomial random variables
Xn, Mn(t) is given as
𝑀𝑛 𝑡 = 𝑞 + 𝑝𝑒𝑡 𝑛 = 1 + 𝑝 𝑒𝑡 − 1 𝑛 𝑎𝑠 𝑞 = 1 − 𝑝
𝑛
λ
= 1 + 𝑛 𝑒𝑡 − 1
based on np=λ .
𝑘 𝑛
Recall that lim 1 + 𝑛
𝑛→∞
= 𝑒𝑘. Letting k=λ(et-1), we have
lim 𝑀𝑛 𝑡 = exp λ 𝑒𝑡 − 1
𝑛→∞
which is the moment generating function of the Poisson random variable.
As an example, when n=10 and p=0.1, we can find the true probability from the binomial
Distribution is 0.73609 for X is less than 2 and the approximate value from the Poisson
Is 0.73575, they are very close. So we can approximate the probability from binomial
Distribution by the Poisson distribution when n is large and p is small.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Example 8.5
In monitoring for a pollution, an experiment collects a small volume of water
and counts the number of bacteria in the sample. Unlike earlier problems, we
have only one observation. For purposes of approximating the probability
distribution of counts, we can think of the volume as the quantity that is
getting large.
Let X denote the bacteria count per cubic centimeter of water and assume that
X has a Poisson probability distribution with mean λ, which we do by showing
𝑋−𝜆
that 𝑌 =
converges in distribution toward a standard normal random
λ
variable as λ tends toward infinity.
Specifically, if the allowable pollution in a water supply is a count of 110
bacteria per cubic centimeter, approximate the probability that X will be at most
110, assuming that λ=100.
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Solution
Answer: We know the mgf for Poisson random variable X is 𝑀𝑋(𝑡) = exp[𝜆(𝑒𝑡 − 1)], thus
We can have the mgf of Y as 𝑀𝑌 𝑡 = exp −𝑡 λ exp[λ(exp(𝑡/ λ)-1)]. The term
(exp(𝑡/ λ)-1) can be written as
𝑡2
𝑡3
exp(𝑡/ λ)−1= t/ λ+2λ +
+ ⋯
Thus MY(t)=exp[−𝑡 λ+ λ(t/
6λ λ 3
𝑡2
𝑡
λ+2λ +
+
6λ λ
𝑡2
⋯ )]=exp[ 2
𝑡3
+
+
6 λ
⋯ )]
When λ∞, MY(t) exp(t2/2)
which is the mgf of the standard normal distribution. So we
can approximate the probability of the Poisson random variable by the standard normal
distribution when λ is large enough (for example, λ≥25).
𝑃 𝑋 ≤ 110 = 𝑃
𝑋−𝜆
λ
≤
110 − 100
= 𝑃 𝑌 ≤ 1 = 0.8413.
10
The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL