* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt - UNT Mathematics
Inductive probability wikipedia , lookup
Random variable wikipedia , lookup
Birthday problem wikipedia , lookup
Infinite monkey theorem wikipedia , lookup
Ars Conjectandi wikipedia , lookup
Probability interpretations wikipedia , lookup
Central limit theorem wikipedia , lookup
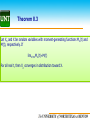
Chapter 8. Some Approximations to Probability Distributions: Limit Theorems Sections 8.2 -- 8.3: Convergence in Probability and in Distribution Jiaping Wang Department of Mathematical Science 04/22/2013, Monday The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Outline Convergence in Probability Convergence in Distribution The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Part 1. Convergence in Probability The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Introduction Suppose that a coin has probability p, with 0≤p≤1, of coming up heads on a single flip. Suppose that we flip the coin n times, what can we say about the fraction of heads observed in the n flips? For example, if p=0.5, we draw different numbers of trials in a simulation, the result is given in the table n 100 200 300 400 % 0.4700 0.5200 0.4833 0.5050 0.02 0.0167 0.005 |%-0.5| 0.03 From here, we can find when n∞, the ratio is closer to 0.5 and thus the difference is closer to zero. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Definition 8.1 In mathematical notations, let X denote the number of heads observed in the n tosses. Then E(X)=np, V(X)=np(1-p). One way to measure the closeness of X/n to p is to ascertain the 𝑋 probability that the distance | − 𝑝| will be less than a pre𝑛 assigned small value ε so that 𝑃 𝑋 𝑛 − 𝑝 < 𝜀 → 1. Definition 8.1: The sequence of random variables X1,X2, .., Xn is said to convergence in probability to the constant c, if for every positive number ε, lim 𝑃 𝑋𝑛 − 𝑐 < 𝜖 = 1 . 𝑛→∞ The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Theorem 8.1 Weak Law of Large Numbers: Let X1,X2, .., Xnbe independent and identical distributed random variables, with E(Xi)=μ and 1 𝑛 2 V(Xi)=σ <∞ for each i=1,…, n. Let 𝑋𝑛 = 𝑋 . Then, for any n 𝑖=1 𝑖 positive real number ε, lim 𝑃 𝑋𝑛 − 𝜇 ≥ 𝜀 = 0 Or 𝑛→∞ lim 𝑃 𝑋𝑛 − 𝜇 < 𝜀 = 1. 𝑛→∞ Thus, 𝑋𝑛 converges in probability toward μ. The proof can be shown based on the Tchebysheff’s theorem with 𝜀 2 2 X replaced by 𝑋𝑛and σ by σ /n, then let 𝑘 = 𝑛. 𝜎 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Theorem 8.2 Suppose that Xn converges in probability toward μ1 and Yn converges in probability toward μ2. Then the following statements are also true. 1. Xn+Yn converges in probability toward u1+u2. 2. XnYnconverges in probability toward u1u2. 3. Xn/Yn converges in probability toward u1/u2, provided u2≠0. 4. Xn converges in probability toward u1, provided P(Xn≥0)=1. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Example 8.1 Let X be a binomial random variable with probability of success p and number of trials n. Show that X/n converges in probability toward p. Answer: We have seen that we can write X as ∑Yi with Yi=1 if the i-th trial results in Success, and Yi=0 otherwise. Then X/n=1/n ∑Yi . Also E(Yi)=p and V(Yi)=p(1-p). Then the conditions of Theorem 8.1 are fulfilled with μ=p and σ2=p(1-p)< ∞ and thus we can conclude that, for any positive ε, limn∞P(|X/n-p| ≥ε)=0. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Example 8.2 Suppose that X1, X2, …, Xn are independent and identically distributed random Variables with 𝐸(𝑋𝑖) = 𝜇1, 𝐸(𝑋𝑖2) = 𝜇2, 𝐸(𝑋𝑖3) = 𝜇3, 𝐸(𝑋𝑖4) = 𝜇4 and all assumed finite. Let S2 denote the sample variance given by 1 𝑆2 = 𝑋𝑖 − 𝑋 2. 𝑛 2 Show that S converges in probability to V(Xi). Answer: Notice that 𝑆2 = 1 1 𝑛 𝑛 2 2 𝑖=1 𝑋𝑖 − 𝑋 where 𝑋 = 1 𝑛 𝑛 𝑖=1 𝑋𝑖 . The quantity 𝑛 𝑛𝑖=1 𝑋𝑖2 is the average of n independent and identical distributed variables of the form 𝑋𝑖2 with E(𝑋𝑖2 )= 𝜇2, and V (𝑋𝑖2 )= 𝜇4 - 𝜇22, which is finite. Thus 1 Theorem 8.1 tell us that 𝑛 𝑛𝑖=1 𝑋𝑖2 converges to 𝜇2 in probability. Finally, based on 1 Theorem 8.2, we can have 𝑆2 = 𝑛 𝑛𝑖=1 𝑋𝑖2 − 𝑋2 converges in probability to 𝜇2 - 𝜇12 =V(Xi). This example shows that for large samples, the sample variance has a high probability of being close to the population variance. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Part 2. Convergence in Distribution The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Definition 8.2 In the last section, we only study the convergence of certain random variables Toward constants. In this section, we study the probability distributions of certain type random variables as n tends toward infinity. Definition 8.2: Let Xn be a random variable with distribution function Fn(x). Let X be a random variable with distribution function F(x). If limn∞Fn(x)=F(x) At every point x for which F(x) is continuous, then Xn is said to converge in distribution toward X. F(x) is called the limiting distribution function of Xn. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Example 8.3 Let X1, X2, …, Xn be independent uniform random variables over the interval (θ, 0) for a negative constant θ. In addition, let Yn=min(X1, X2, …, Xn). Find the limiting distribution of Yn. Answer: The distribution function for the uniform random variable Xi is 0, 𝑥 < 𝜃 𝐹(𝑋𝑖) = 𝑃(𝑋𝑖 ≤ 𝑥) = 𝑥−𝜃 , −𝜃 𝜃≤𝑥≤0 1, 𝑥 > 0. We know 𝐺 𝑦 = 𝑃 𝑌𝑛 ≤ 𝑦 = 1 − 𝑃 𝑌𝑛 > 𝑦 = 1 − 𝑃 min 𝑋1, 𝑋2, … , 𝑋𝑛 > 𝑦 = 1 − 𝑃 𝑋1 > 𝑦 𝑃 𝑋2 > 𝑦 … 𝑃 𝑋𝑛 > 𝑦 = 1 − 1 − 𝐹𝑋 𝑦 𝑛 0, 𝑦 < 0 0, 𝑦 < 0 = 1− 𝑦 𝑛 , 𝜃 𝜃 ≤ 𝑦 ≤ 0 so we can find lim 𝐺(𝑦) = 1, 𝑦 > 0. 0, 𝑦 < 𝜃 = 1, 𝑦 ≥ 𝜃. 𝑛→∞ lim 1 − 𝑛→∞ 𝑦 𝑛 , 𝜃 𝜃≤𝑦≤0 1, 𝑦 > 0. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Theorem 8.3 Let Xn and X be random variables with moment-generating functions Mn(t) and M(t), respectively. If limn∞Mn(t)=M(t) For all real t, then Xn converges in distribution toward X. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Example 8.4 Let Xn be a binomial random variable with n trials and probability p of success on each trial. If n tends toward infinity and p tends zero with np remaining fixed. Show that Xn converges in distribution toward a Poisson random variable. Answer: We know the moment-generating function for the binomial random variables Xn, Mn(t) is given as 𝑀𝑛 𝑡 = 𝑞 + 𝑝𝑒𝑡 𝑛 = 1 + 𝑝 𝑒𝑡 − 1 𝑛 𝑎𝑠 𝑞 = 1 − 𝑝 𝑛 λ = 1 + 𝑛 𝑒𝑡 − 1 based on np=λ . 𝑘 𝑛 Recall that lim 1 + 𝑛 𝑛→∞ = 𝑒𝑘. Letting k=λ(et-1), we have lim 𝑀𝑛 𝑡 = exp λ 𝑒𝑡 − 1 𝑛→∞ which is the moment generating function of the Poisson random variable. As an example, when n=10 and p=0.1, we can find the true probability from the binomial Distribution is 0.73609 for X is less than 2 and the approximate value from the Poisson Is 0.73575, they are very close. So we can approximate the probability from binomial Distribution by the Poisson distribution when n is large and p is small. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Example 8.5 In monitoring for a pollution, an experiment collects a small volume of water and counts the number of bacteria in the sample. Unlike earlier problems, we have only one observation. For purposes of approximating the probability distribution of counts, we can think of the volume as the quantity that is getting large. Let X denote the bacteria count per cubic centimeter of water and assume that X has a Poisson probability distribution with mean λ, which we do by showing 𝑋−𝜆 that 𝑌 = converges in distribution toward a standard normal random λ variable as λ tends toward infinity. Specifically, if the allowable pollution in a water supply is a count of 110 bacteria per cubic centimeter, approximate the probability that X will be at most 110, assuming that λ=100. The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL Solution Answer: We know the mgf for Poisson random variable X is 𝑀𝑋(𝑡) = exp[𝜆(𝑒𝑡 − 1)], thus We can have the mgf of Y as 𝑀𝑌 𝑡 = exp −𝑡 λ exp[λ(exp(𝑡/ λ)-1)]. The term (exp(𝑡/ λ)-1) can be written as 𝑡2 𝑡3 exp(𝑡/ λ)−1= t/ λ+2λ + + ⋯ Thus MY(t)=exp[−𝑡 λ+ λ(t/ 6λ λ 3 𝑡2 𝑡 λ+2λ + + 6λ λ 𝑡2 ⋯ )]=exp[ 2 𝑡3 + + 6 λ ⋯ )] When λ∞, MY(t) exp(t2/2) which is the mgf of the standard normal distribution. So we can approximate the probability of the Poisson random variable by the standard normal distribution when λ is large enough (for example, λ≥25). 𝑃 𝑋 ≤ 110 = 𝑃 𝑋−𝜆 λ ≤ 110 − 100 = 𝑃 𝑌 ≤ 1 = 0.8413. 10 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL