Download BASIC SENSORS

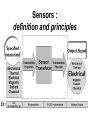
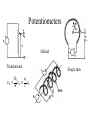
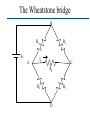
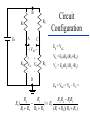
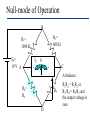
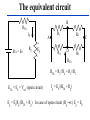
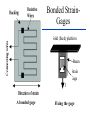
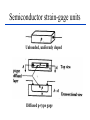
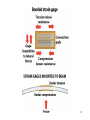
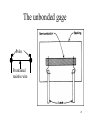
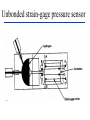
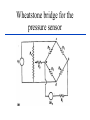
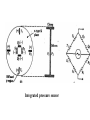
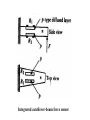
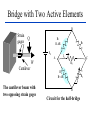
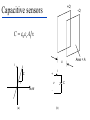
BASIC MECHANICAL
SENSORS
AND
SENSOR PRINCIPLES
Definitions
• Transducer: a device that converts one form
of energy into another.
• Sensor: a device that converts a physical
parameter to an electrical output.
• Actuator: a device that converts an
electrical signal to a physical output.
Sensors :
definition and principles
Sensors : taxonomies
• Measurand
– physical sensor
– chemical sensor
– biological sensor(cf : biosensor)
• Invasiveness
– invasive(contact) sensor
– noninvasive(noncontact) sensor
• Usage type
– multiple-use(continuous monitoring) sensor
– disposable sensor
• Power requirement
– passive sensor
– active sensor
Potentiometers
Helical
Translational
𝑅𝑖
𝑥𝑖
𝑣0 = 𝑣𝑠 = 𝑣𝑠
𝑅
𝑙
Single turn
The Wheatstone bridge
B
R1
Eb
A
R2
Ig
C
Rg
R4
R3
D
B
R2
R1
A
Eb
C
E0 = VAC
+ VAC R4
Circuit
Configuration
+
VA
-
+
VC
D
VA = EbxR4/(R1+R4)
R3
VC = EbxR3/(R2+R3)
E0 = VAC = VA – VC =
R4
R3
R2 R4  R1R3
Eb (

)  Eb
R1  R4 R2  R3
( R1  R4 )( R2  R3 )
Null-mode of Operation
B
R2 =
600 
R1 =
1000 
Eb=
10 V A
Ig
0
-
C
+
At balance:
R4 =
Rx
R3
D
R2R4 = R1R3 or
R1/R4 = R2/R3 and
the output voltage is
zero
B
Example 1
Assume that the bridge shown is
used to determine the resistance of
an unknown resistance Rx. The
variable resistance is the
resistance box that allows
selection of several resistors in
series to obtain the total resistance
and it is set until null position in
the meter observed. Calculate the
unknown resistance if the variable
resistance setting indicates
625.4.
R2=
600 
R1=
1000 
Eb=
10 V
Ig
A
0
-
C
+
R4=
Rx
R3
D
The bridge will be balanced
if R1/R4 = R2/R3 .
Hence,
R4 = Rx = R1/(R2/R3) =
1000x625.4/600 = 1042.3 .
9
Deflection-mode of Operation
All resistors can very around their nominal values as R1 + R1,
R2 + R2, R3 + R3 and R4 + R4. Sensitivity of the output
voltage to either one of the resistances can be found using the
sensitivity analysis as follows
E0
 R3 ( R1  R4 )( R2  R3 )  ( R2  R3 )(( R2 R4  R1 R3 )
S R1 
 Eb
R1
( R1  R4 ) 2 ( R2  R3 ) 2
R4
  Eb
( R1  R4 ) 2
S R3
S R2
E0
R2

  Eb
R3
( R2  R3 ) 2
E0
R3

 Eb
R2
( R2  R3 ) 2
S R4
E0
R1

 Eb
R4
( R1  R4 ) 2
The equivalent circuit
B
RT h
Ig
ET h = E0
Rg
A
+
Eg
-
R1
R4
R2
D
R3
RT h
RTh = R1//R4 + R2//R3
ETh = E0 = VAC (open circuit)
Ig = E0/(RTh + Rg)
Eg = E0Rg/(RTh + Rg) In case of open-circuit (Rg) Eg = E0
C
Stress and strain
T
L
D
A metal bar
Tension: A bar of metal is subjected to a force
(T) that will elongate its dimension along the
long axis that is called the axial direction.
Compression: the force acts in opposite
direction and shortens the length
Stress: the force per unit area
a = T/A (N/m2)
L+dL
L
dL
T
Strain
A
L
T
Bar with tension
Strain: The fractional change in length
a = dL/L (m/m)
Breaking
point
Stress
(a)
Elastic
Limit
Strain
Elastic
Region
Plastic
Region
( a)
The stress-strain relationship
Hooke’s law
Stress is linearly related to strain for elastic materials
a = a /Ey = (T/A)/Ey
Ey : modulus of elasticity ( Young’s modulus)
Transverse strain
The tension that produces a strain in the axial direction causes
another strain along the transverse axis (perpendicular to the axial
axis) as
t = dD/D
This is related to the axial strain through a coefficient known as the
Poisson’s ratio as
dD/D = - dL/L
The negative sign indicates that the action is in reverse direction,
that is, as the length increases, the diameter decreases and vice
versa. For most metals  is around 0.3 in the elastic region and 0.5
in the plastic region
Electrical Resistance of Gage Wire
R
R
R
dR 
d 
dL 
dA

L
A
T
L
D
R=L/A
L

L
dR  d  dL  2 dA
A
A
A
dR d dL dA



R

L
A
A = r2 = (/4)D2 and dA/A = 2 dD/D yields dD/D = - dL/L
dR d dL


(1  2 )
R

L
Piezoresistive effect
Dimensional effect
Principles of strain measurement
K = (dR/R)/(dL/L) = (dR/R)/a
Gage factor - K
For wire type strain gages the
dimensional effect will be
dominant yielding K 2
For heavily doped semiconductor type gages the piezoreziztive effect
is dominant yielding K that ranges between 50 and 200
dR can be replaced by the incremental change R in this linear
region yielding R/R = Ka
Bonded StrainGages
Solid (fixed) platform
Beam
Strain
Gage
T
A bonded gage
Fixing the gage
Examples of bonded gages
Resistance-wire type Foil type
K  2.0
R0 = 120  or
350 . 600 
and 700  gages
are also available
Helical-wire type
Semiconductor strain-gage units
Unbonded, uniformly doped
Diffused p-type gage
Solid (fixed) platform
Fixing the gage
Beam
Strain
Gage
T
20
21
Strain gage on a
specimen
22
The unbonded gage
Poles
Prestrained
resistive wire
23
Unbonded strain-gage pressure sensor
Example 2
A strain gage has a gage factor 2 and exposed to an axial strain
of 300 m/m. The unstrained resistance is 350 . Find the
percentage and absolute changes in the resistance.
a = 300 m/m = 0.3x10-3;
R/R = Ka = 0.6x10-3 yielding
%age change = 0.06% and R = 350x0.6x10-3 = 0.21 .
25
Example 3
A strain gage has an unstrained resistance of 1000  and gage
factor of 80. The change in the resistance is 1 when it is
exposed to a strain. Find the percentage change in the
resistance, the percentage change in the length and the external
strain (m/m).
R/R (%) = 0.1 %;
L/L (%) = [R/R (%)]/K = 1.25x10-3%, and
a = [L/L (%)]/100 = 1.25x10-5 = 12.5 m/m
26
Wheatstone bridge for the
pressure sensor
Integrated pressure sensor
Integrated cantilever-beam force sensor
Elastic strain-gage
Mercury-in-rubber strain-gage
plethysmography (volumemeasuring) using a four-lead gage
applied to human calf.
Venous-occlusion plethysmography
Arterial-pulse plethysmography
Effect of Temperature and Strain
in other Directions
R  R0[1   (T  T0 )]
R0 is the resistance at T0 and
 is the temperature
coefficient
This is very much pronounced in case of semiconductor
gages due to high temperature coefficient.
Effects of wanted strain (sw), unwanted strain (su) and
temperature (T) add up in the change in resistance as
R = Rsw + Rsu + RT
The effect of unwanted strain and temperature must be
eliminated before the resistance change is used to indicate the
strain
Bridge Configurations For Strain
Gage Measurements
B
Solid platform
Strain
gage
R1
R2
Q
Eb
A
Ig
C
Rg
W
Cantilever
R3
R4 = Rx
D
The cantilever beam with a
single strain-gage element
A quarter bridge
Analysis of quarter-bridge circuit
Let R1 = R2 = R3 = R and R4 = Rx = R + R = R(1 + R/R), and
let x = R/R. The open circuit voltage E0 = 0 at balance (R = 0).
At slight unbalance (R  0)
R2 R4  R1R3
R( R  R)  R 2
R
E0  Eb
 Eb
 Eb
( R1  R4 )( R2  R3 )
( R  R  R)( R  R)
2(2 R  R)
Let x = R/R
x 1
(1  )  1 
2
x
x
E0  Eb
 Eb
x
2(2  x)
4(1  )
2
2
2
3
x x
E
x
x
  ... E0  b ( x    ...)
2 4
4
2
4
Since x<<1, higher order terms
can be neglected yielding
Eb
Eb R
E0 
x
4
4 R
Sensitivity analysis
Sensitivity analysis can also be used
S R4
E0
R1

 Eb
2
R4
( R1  R4 )
E0  R4 S R4
R
Eb R
 Eb
R 
2
( R  R)
4 R
Effect of Temperature and
Tensile Strain
• R = RQ + RW + RT
• The effect of unwanted strain and temperature must be
eliminated.
• The circuit as it is provides no compensation.
• Using a second strain gage of the same type for R1 can
compensate effect of temperature.
• This second gage can be placed at a silent location
within the sensor housing, hence kept at the same
temperature as the first one.
• As a result, both R1 and R4 have the same amount of
changes due to temperature that cancel each other in the
equation yielding perfect temperature compensation
Wheatstone Bridge with Strain Gages
and Temperature Compensation
36
Bridge with Two Active Elements
B
Strain
gages
Q
R1
R-R
Eb
A
R2
Ig
W
Cantilever
The cantilever beam with
two opposing strain gages
C
Rg
R4
R+R
R3
D
Circuit for the half-bridge
Circuit analysis
Let R2 = R3 = R; R1 = R - R; R4 = R + R, the open circuit
voltage E0 = 0 at balance (R = 0). At slight unbalance (R  0)
B
R2 R4  R1 R3
E0  Eb
( R1  R4 )( R2  R3 )
R( R  R)  R( R  R)
 Eb
( R  R  R  R)( R  R)
2R Eb R
 Eb

4R
2 R
R1
R-R
Eb
A
R2
Ig
C
Rg
R4
R+R
R3
D
Insensitivity of half-bridge
Wanted
strain
Unwanted
strain
Temperature
R4
R1
Effects of wanted and unwanted strains
and temperature on measuring gages
Bridge with Four Active
Elements (Full Bridge)
Q
R2
R4
R1 R3
W
The cantilever beam with four
strain gages (full bridge)
The force, when applied in the
direction shown, causes
tension on gages at the top
surface (R + RQ) and
compression on gages at the
bottom surface (R - RQ).
The tensile force W causes (R +
RW) on all gages.
The temperature also produces
(R + RT) on all gages.
B
R2
R+R
R1
R-R
Eb
A
Ig
C
Rg
R4
R+R
R3
R-R
D
R2 R4  R1R3
E0  Eb
( R1  R4 )( R2  R3 )
 Eb
•The strain gages that are
working together are placed
into opposite (nonneighboring) arms of the
bridge.
•The strain gage resistors are
manufactured for a perfect
match to have the open circuit
voltage E0 = 0 at balance (R
= 0).
•At slight unbalance (R  0)
with R1 = R3 = R - R; R2 =
R4 = R + R
( R  R)( R  R)  ( R  R)( R  R)
R
 Eb
( R  R  R  R)( R  R  R  R)
R
Inductive sensors
L = n2G, where
n= number of turns of coil
G = geometric form factor
 = effective permeability
Self-inductance
Differential transformer
Mutual inductance
LVDT
transducer
(a) electric diagram
and
(b) cross-section
view
LVDT
+Q
Capacitive sensors
Q
C   0 r A x
Area = A
x
i
v
1
dv/dt
(a)
i
+
C
C

(b)
Capacitive displacement transducer
(a)single capacitance and
(b)differential
capacitance
sensitivity  K 
C
A
  0 r 2
x
x
dC
C
  or
dx
x
dC
dx

C
x
V0 ( j )

X I ( j )
(E
x0
) j
Capacitive sensor for measuring
dynamic displacement changes
j  1
where   RC 
R 0 r A
x0
q  kf
k is piezoelectric
constant C/N
kf
kfx
v

C  0 r A
q  Kx
dq
dx
is 
K
 iC  iR
dt
dt
K is proportionality
constant C/m
1
v0  vC ( )  iC dt
C
dv
dx v0
 is  i R  C ( 0 )  K

dt
xt R
V0 ( j ) K S j

X ( j ) j  1
Piezoelectric sensors
KS=K/C, V/m;  = RC, s
Response to step displacement
High-frequency response
High-frequency circuit
model for piezoelectric
sensor. RS is the sensor
leakage resistance and
CS the capacitance. Lm,
Cm and Rm represent
the mechanical system.
Piezoelectric sensor frequency
response.
Quantum Tunneling Composites
(a) Structure
(b) Effect of pressure
Structure and effect of pressure for QTC
51
Effect of Pressure on a QTC Pill
52
QTC as a Pressure Sensor
53