Download Energy - Stamford High School

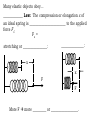
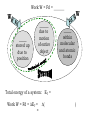
Work W = the transfer of energy E
Work done _____ a system ____________ its total energy.
Work done _____ a system _____________its total energy
W done on system:
W done by system:
Box now
has ______
energy
box
d
d
box
Box now
has _____
energy
piling
Ex. A 200-N box is pushed 8.0 m along a floor by a
horizontal 75-N force. How much work was done?
200
N
W=
=
F = 75 N
=
•1 newton·meter equals 1 ___________:
1 Nm = 1 ____
•So the answer can be written: W = __________
• Both Nm and J are _______________.
•To express them in terms of fundamental units,
write:
1 J = 1 Nm
= 1 (_________)(__)
= 1 ____________
Plot the force and distance from the previous example.
F (N)
d (m)
What does the grey area represent?
area = L W = (
area = LW =
)(
=
)=

=
Note:
1/ In the equation:
But in the answer:
J = Ft,
W = 600 J,
J represents the
quantity ___________.
J represents the
unit _____________.
2/ If you substitute F = 1 N and d = 1 m, you get:
W = Fd = (
)(
)=
1 joule is the work done (or energy needed) in lifting
1 ____________________ to a height of _______________ .
3/ Joules are metric ____________ units. Americans use
____________ for energy units. Foods rated in calories in
the US are rated in joules in the ________________________.
4/ Work W and energy E are ___________. They do
NOT have _____________, even though F and d do.
5/ What is the value of work W = Fd when d = 0?
W=
.
This is b/c there is _________ if d = 0.
6/ The equation W = Fd is only valid when
F and d are parallel:
F
or
F
When F and d are NOT parallel…
…then the "real" equation for W must be used:
W=
, where q is the angle between F and d
F
q
d
The equation W = Fd is ok to use here only if _____ is
replaced by the __________________in the direction of d:
W = Fd = _________, which is the same as the one above.
The equation W = __________ explains why the work W
that you do on a box is ____________ when you carry it
horizontally at _______________________:
F you exert
to hold
W = Fdcosq
=
d
w
=
=
Another way to see that W must equal 0:
Given W = DET, doing work should change __________.
But the energy E of box _______________________ as it
is carried horizontally, so DET = ____ and so W = ____.
Which does more work, lifting a 30-N box a vertical
distance of 2-meters at a constant speed of…
…. 0.5 m/s
or
…1.0 m/s?
In both cases, constant v  a = ___  Fnet = ____.
F exerted against gravity = ______
BOTH
CASES:
30
N
w = 30 N
The W done against gravity:
W=Fd = (
)(
)=
The distance 2 m will be covered in less ______ in case A,
but W is ___________________ for both cases.
Power P:
the rate at which ___________________
the rate at which _________ is transferred
P =
Power is a _____________—it has ___________________.
If time t is constant:
P
If work W is constant:
P
W
t
Ex: When Harry Potter lifts Draco Malfoy on his
broomstick, 1400 J of work is done in 2.5 seconds.
How much power did his broomstick develop?
Unknown:
Given:
Equation:
P=?
W=
P=
=
=
t=
•1 joule/second equals 1 _____________:
1 J/s =
•So the answer can be written: P =
•Both J/s and W are ____________________.
•To express them in terms of fundamental units,
write:
1W=
=
=
=
Note:
1/ In the equation:
But in the answer:
And in:
P = W/t,
W represents the
quantity _________.
P = 560 W,
W represents the
unit ______________.
w = 30 N
w represents the
quantity _________ .
2/ If you substitute F = 1 N, d = 1 m and t = 1 s,
you get:
P = Fd/t = ( )(
)/
=
=
1 watt is the power developed in raising 1 ______
_____________ to a height of 1 _________ in 1 _________.
3/ To remember that 1 watt = 1 joule per second:
Work W = Fd = _______  The work done on a system
can going into changing its potential energy PE, its
kinetic energy KE, and/or its internal energy Q.
W
W
____
stored up
due to
_________
____
due to
______
of ____
object
____
within
molecular
and atomic
_____
Total energy of a system: ET =
_______________ energy
_______________ PE - "position" energy an object has
due to work done against _____________
Raise a box
at constant v:
W done on system:
F
W= F d
=
Dh
F
box
=
w=
Box has gained PE due to
work done on it:
DPE =
PE
DPE =
m
PE
PE
Dh
v
Ex: Calculate the PE of a 3500-kg cockroach when
it climbs to a height of 45 m above the ground.
DPE =
=
=
Note:
1/ PE (like any energy) is a _______—it has no __________.
2/ The units: kg m2/s2 must equal 1 ________.
So the answer can also be written:
DPE = 1.5 x 106 ___
or
DPE = 1.5 _____
3/ How much work did the cockroach do against
gravity in order to increase its PE by this amount?
W = __________________
Sometimes this equation is written without the D's:
=
The "h" or Dh" refers to the height above a zero
“_________________," especially during changes in height.
Ex: a pendulum swings back and forth
Using the table
top as zero level:
Using the floor
as zero level:
Dh =
=
Dh =
=
1m
ceiling
0.6 m
1.6 m
0m
1m
Table
floor
0m
Gravitational PE does not depend on ______________.
Both boxes below gain the _______________________
of potential energy.
same Dh
5 kg
5 kg
ground
Dh is used to emphasize that it is only the ___________
change in height that matters—not the _________ taken.
_________________ KE - "motion" energy that an object
has due to being _____________________ to a speed v
d
F
1 kg
Work done W = Fd = __________
Equation for
kinetic energy:
units:
KE =
[KE] = (1/2) [
=
=
=
] [
(
)(
]2
)2
Ex. Determine the KE of Dobby, the 22-kg elf flying
at a speed of 9.0 m/s at a height of 35 m above ground.
KE =
=
=
=
Note:
1/ KE (like any energy) is a ________—it has no _________.
2/ How much work was done on the elf in order to
increase its KE to this amount?
W=
=
KE
KE
m
v
Ex: A rabbit has 5.0 J of KE when running at a
speed of 2.0 m/s. If the rabbit increases its speed
to 4.0 m/s, what will the new KE be?
double v  _____________ KE

Ex: A ball is thrown straight up.
What happens to its KE as it rises?
What is its KE when it reaches its maximum height?
What happens to its KE as it falls back down?
Compare its KE at the instant it is thrown up to its
KE when it returns back to the same place it was
thrown from.
Why study springs?
Springs are ___________. Many things have some
elasticity, and so they behave like springs:
•wood
•metal
•________________
•concrete
•humans
•water
•________________
•atoms
•musical instruments  strings, air, drums…
•quartz
•speakers
•etc, etc, etc
Many elastic objects obey…
_____________ Law: The compression or elongation x of
an ideal spring is ________________________ to the applied
force Fs.
Fs =
stretching or ________________:
_______________:
x
x
F
F
More F  more _________ or __________________.
Ex. A weight of 8.7 N is attached to a spring that
has a spring constant of 190 N/m. How much
will the spring stretch?
w/ weight
w/o weight
Given:
Fs =
k=
Unknown:
x =?
Equation:
Fs =
=
=
x
8.7
N
Fs =
Fs
Ex: A force of 5.0 N
causes the spring to
stretch 0.015 m.
How far will it stretch
if the force is 10 N?
x
What quantity does the slope represent?
slope =
=
Compare to Fs = kx
Solve for Fs/x = k
The slope represents ________________________ , ___.
What are the units of the spring constant, k?
Solve…
Fs = kx
…for k:
k =
units of k:
[k] = [
=
]/[
/
]
(____________)
This can be also seen from the graph:
Fs (N)
k = the slope = ________
So k has the same
units as _________:
x (m)
Hooke's Law:
Fs = kx
Fs
Imagine a spring
for which you
have to apply more
force to get it to
stretch as much as
spring A…
x
stiffer spring  _____________  ____________
Elastic PE - the energy stored in a spring when work
is done on it to stretch or compress it
PEs =
Ex. A spring with a spring constant of 370 N/m is
stretched a distance 6.4 x 10-2 m. How much elastic
PE will be stored in the spring?
PEs =
=
=
=
How much work was done to stretch the spring by
this amount?
W=
PEs = (½)kx2
PES
What happens to PEs
when you double x?
The PEs ______________.
When you triple x?
x
________ more PEs.
Ex: The elastic PE stored in a spring is 0.70 J when
it is stretched 0.010 cm. If the same spring is stretched
0.030 cm, how much PE will then be stored in it?
x changes from 0.010 to 0.030 


=
Ex: Plot F vs. x for
an ideal spring
F
x
What does the grey area represent?
area = (½)bh =
=
=
=
 It represents ____________________________________.
One last warning:
If a spring is stretched too much, it _______________
permanently, and Hooke's Law (Fs = kx ) is ________
_____________
Which of the graphs below shows a spring that
obeys Hooke's Law?
F
F
x
x
F
F
x
x
Work W = Fd = _______
W
W
_____
stored up
due to
position
______
due to
motion
of entire
object
_____
within
molecular
and atomic
bonds
Total energy of a system: ET =
Work W = Fd = DET =
=
D(
)
DPE =
_________________:
DPE =
__________________:
DPE =
Work W = Fd = DET
acceleration
motion of ____________:
DKE =
DQ  ____________
 Dinternal energy
 DKE of _______/molec.
or DPE or ________
 increase ________
or change __________
What kind of energy does your work change
if you….
1/ …lift an object at a constant speed?



2/ …accelerate an object at a constant height?



3/ …drag an object across a surface at a constant speed
and height?
 constant v  ____________
 constant h  ___________
 DQ only  energy from work against ___________
goes into raising _____________or changing _______
Work done on a system  DET
However, if _______ work is done on a system, then its
total energy ET cannot change—it _____________________.
In other words, get rid of the "external work,"
and the total energy ET will _____________________________
PE
stored up
due to
position
KE
due to
motion
of entire
object
Q
within
molecular
and atomic
bonds
The Law of Conservation of Energy:
The total energy of an isolated system of bodies
remains constant.
before
=
after
=
=
If there is no friction, DQ = _____ 
=
=
mechanical
energy ______
mechanical
energy ________
Notice the similarity between:
…the Conservation of Energy:
PE
+ KE
=
PE' + KE'
…and the Conservation of Linear ________________:
=
•Momentum conservation is used to determine what
happens to objects after they _________________________.
•Energy conservation is also used to determine what
happens to objects ______________________________.
•Both _________________ and __________ are useful ideas
because they allow us to ignore ___________, which can
be very complicated.
Restatements of the…
Law of the Conservation of Energy:
"The total energy is neither __________________ nor
__________________________ in any process."
"Energy can be __________________ from one form to
another and _______________ from one body to another,
but the __________ amount remains ________________."
"Energy is neither _____________ nor _______________."
Ex: A pendulum swings back and forth. It position at
two points is shown below. Ignore friction. What energy
does it have at each position?
Use:
=
When it reaches
maximum height:
PE =
(given)
KE = ____
ET = _____
PEtop
=>
When it reaches
minimum height:
PE' =
KE' =______
ET' =
Ex: A 0.25-kg box is released from rest and slides
down a frictionless incline. Find its speed as it
arrives at the bottom of the incline.
Use:
=
4.0 m
When the box is released at the top:
PE =
=(
KE =_______
ET =
)(
)(
) =
Just before it hits bottom:
PE' = ?
KE' = ?
ET ' = ?
PEtop =>
Now use KE = ___________ to find v:
KE =
=
=
=
Ex: Drop a 2.0 kg rock off of a 15-m cliff.
Use g ≈10 m/s2 to simplify.
Do not ignore air resistance.
PE =
=(
KE =____
ET =
)(
)(
)=
15 m
Just before it hits:
PE =
Suppose KE =
ET =
How much energy is "missing?"
And where did it go?
How will it affect v at bottom?
(PEtop ≠ KEbottom)
Ex: The mass m is not really needed to find the
speed v when using the Conservation of Energy
with gravitational PE and no friction:
PEtop => KEbottom
top
h
bottom
ET (top)
PE + KE
=
=
=
=
=
=
ET (bottom)
PE' + KE'
Ex: A spring with a spring constant of 220 N/m is
compressed a distance 0.035 m as shown below. A
mass of 0.027 kg is place against it on a frictionless
slide. When the mass is released: 1/ how fast will it
go as it leaves the spring, and 2/ how high up the slide
will it go before it stops and comes back down?
m
energy stored
in spring
energy of mass
as it starts moving
energy of mass
at highest point


=
=
1/ How fast will the mass be going as it leaves the
spring?
=
=
=
=
2/ How high up the slide will it go?
=
=
=
=
Ex. Mr. Butchko is fired out of a cannon at 3 different
angles with the same speed from a cliff.
1/ For which angle will he hit the ground with the
most speed?
2/ For which angle will he hit the ground in the least
time?
1
2
3