Download Scaling and the Solar System

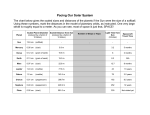
Name: __________________
Lab Partners: __________________
Instructor's Signature: __________________
Lab Title: Scaling and the Solar System
Equipment:
Scientific calculator
Rulers
Computer with web access and Java-compatible browser
Meter sticks
Calipers
Spherical objects of various sizes:
Plastic and Styrofoam balls, metal pellets, table salt, seeds, etc.
Introduction:
In this lab we will try to understand distances and sizes in the solar system
by creating a scale model. While even our model will get rather large in
human terms, it should help you relate astronomical distances, such as the
Earth-Sun distance, to distances that are a bit easier to comprehend.
Hopefully, this lab will help you to think in terms of comparisons (such
as that Jupiter is about five times farther from the Sun than the Earth is)
rather than in absolute numbers (such as 780 million kilometers). To make
sure that you are familiar with both methods, work through the Pre-lab
Exercises before completing the rest of this lab.
The essence of building your models will be to compute the scale factor.
This is the number by which you multiply a linear dimension in the actual
object to get the corresponding dimension in a model.
Say, for example, you were building a 1:32 scale model of a locomotive.
The numbers given above indicate that one inch on your model corresponds
to 32 inches on the actual locomotive (the inches are just for
illustration—the scaling also applies for feet, centimeters, furlongs, etc.).
The scale factor for this model is
-1-
SF =
1
= 0.03125
32
To find the size of a part on your model, you would multiply the linear size
of the part on the actual locomotive by 0.03125 (try this for something on
the locomotive that is 32 feet in length, and you should find that it would be
one foot long on the model).
A similar scale factor is the scale on highway maps, such as, for example,
1 inch = 100 miles (or 1 cm = 50 kilometers for a typical metric map). In
the metric case, the scale factor for the entire map would be:
SF = 1 cm/50 km = 1 cm/5,000,000 cm = 2 × 10 -7.
Try this on your calculator and see if you get the same answer. To carry the
analogy a bit further, imagine that the actual distance between two cities, say
London to Edinburgh, was 500 km. How far apart should the map maker
place them on the map? To find out, the map maker would multiply the
actual distance (500 km) by the scale factor.
500 km × (1 cm/50 km) = 10 cm.
The same result can also be obtained by direct multiplication:
500 km × (2 × 10 -7) = 0.0001 km = 0.1 m = 10 cm.
In this lab, we will want to use the numerical value of the scale factor itself
(i.e., 2 × 10 -7 for the above example) rather than the ratio (i.e., 1 cm/50 km).
This will only come out properly if you use the same units (i.e., meters) for
both the numerator and the denominator before you perform the
division.
The Solar System is a bit larger than either a locomotive or the region
covered by a road map, and so the scale factor of your model is going to be
much smaller in order to build a model that you can begin to comprehend.
Let’s say that you use a ball to represent the Sun, and that the diameter of the
ball is 10 cm (about 4 inches). The scale factor for your model Sun is the
diameter of the ball divided by the actual diameter of the Sun. From a text,
you can find that the diameter of the Sun is about 1.392x106 km. You must
first convert that into centimeters, the same units as you used to measure the
ball, and so you multiply by the number of centimeters in a kilometer, or
105 , to get 1.392x1011 cm for the diameter of the Sun. Your scale factor is
then:
SF =
10cm
= 7.18 × 10 −11
11
1.392 × 10 cm
-2-
Your numbers below will be different! Note that we have kept only
three significant figures in the answer above, one more than in the least
accurate number used in the calculation. Model sizes calculated with this
scale factor shall only be accurate to two significant figures.
Now, to build your model Solar System, you scale everything else down
by the same amount, ie. all sizes and distances in the Solar System must be
multiplied by your scale factor. For example, the radius of Neptune’s orbit
9
9
around the Sun is 4.5x10 km, and its diameter is about 50,000 km (or 5x10
cm). Multiplying by the scale factor gives 0.32 km and 0.36 cm for the
orbital radius and diameter of Neptune in your model (check that you get
these results if you need practice with your scientific calculator). In your
model, then, with a 10 cm ball representing the Sun, Neptune would be
about two tenths of a mile away, and would be about the size of a small ball
bearing.
Procedure:
Step 1. Each group shall initially be assigned a large ball to represent the
Sun. For this part of the lab, we want to make sure that you can go through
the process of computing a scale factor for a model which uses the ball you
have been assigned as the Sun. To do this, you need to measure (using the
large calipers) the diameter of the ball representing the Sun and then
determine the overall scale factor, SF, from the relation:
Your Scale Factor
= SF =
Your measured diameter of large ball (in meters)
1,392,000,000 m
Note that this is the scale factor for all sizes and distances in your scale
model. As you complete this lab, it will become obvious why the largest
object available determines the overall scale of your entire "solar system".
Calculate your scale factor in the space below and round off the final
result to three significant digits (note that we’ve changed units from the
example used in the introduction):
Your Scale Factor
= SF =
m =
1.392 × 10 m
9
Ask your classmates or your instructor if you are not sure how to do the rounding.
-3-
Step 2. Use Your Scale Factor calculated above to compute model values
for the diameter and orbital radius of the Earth in the box below. Note that
the scaled diameter of a planet is equal to the actual diameter of a planet
multiplied by Your Scale Factor. Similarly, the scaled distance from the
Sun to a planet would be the actual distance to the planet multiplied by
Your Scale Factor.
Example: Using the scale factor obtained for the 10-cm diameter ball
representing the Sun, the scaled diameter of the Earth would be:
Scaled Diameter of the Earth
= 1,275,600,000 cm × 7.18 × 10-11
= 0.092 cm = 0.92 mm
The scaled distance from the Sun to the Earth in this example would be:
Scaled Distance to the Earth
= 149,000,000,000 m × 7.18 × 10-11
= 10.7 m
Remember to use Your Scale Factor in computing the scaled diameter and
orbital radius of the Earth in Table 2. Don't use the factor 7.18 × 10 -11
shown in the sample calculation above.
Using Your Scale Factor, what are the model values for the diameter and
orbital radius of Earth? Show your work, and write down your units!
Model diameter of Earth:
Model orbital radius of Earth:
Step 3. Now it gets easier. Fire up the web browser on one of the lab
computers (your instructor can show you where it is if the launcher isn’t
running). Go to the site:
http://www.exploratorium.edu/ronh/solar_system/index.html
(either your neighbors or your instructor can help you if you’re not familiar
with web browsers). Scroll down to the “Solar System Model.” In the blank
box next to “Sun,” below where it says “Body Diameter in mm,” enter the
diameter which you measured for the ball which your group was assigned as
the Sun (watch out for the change in units!).
-4-
How do the scaled diameter and orbital radius for Earth given on the
web page compare to the values you computed above? Are they close?
Write your answer here.
Do you believe that you would have an easy time finding an object to
represent Earth in this model? Why or why not?
Step 4. For this part, all groups should use the largest rubber ball to
represent the Sun. This should give scaled Solar Systems identical for each
group. Measure the size of the largest ball, and repeat the process of Step 3.
The Java script on the web page now calculates a scaled model of the Solar
System, based upon having the large ball represent the Sun. Use the
numbers to complete Table 2. You can also print out the web page, but be
sure that it prints properly before you exit the web site. Before proceeding,
answer the questions below.
Look near the bottom of the screen. The script has also calculated the
scaled speed of light in your model. What is its value?
How long would it take a light beam to travel from the Sun to Pluto in
your model (don’t forget the units)? To find out, simply divide the scaled
distance of Pluto from the Sun by the scale speed of light. How do you
believe this compares to the actual light travel time from the Sun to Pluto?
Time =
dis tan ce
=
speed
-5-
Step 5. Now, measure (using the metal calipers) and select smaller objects
of appropriate sizes to represent the nine planets and complete the third
column in Table 2. Try to find small objects as close as possible in
measured size to the scaled diameters you calculated in the first column of
Table 2.
In the last column of Table 2, say which objects you used to represent
the Sun and each of the nine planets in your model solar system. Also
comment on how close the measured diameters of each of your selected
objects are to being the correct scaled size as calculated in Table 2.
Step 6. After the completion of Table 2, show your instructor and then take
the selected objects outside and place them at their proper scaled distances
from the Sun. Your instructor will place the "Sun" under a light so that you
can see it.
Use the meter sticks to determine the distances to the inner terrestrial
planets. When that runs out, you can just pace off the scaled distances to the
outer planets using one pace equal to one meter. Stop when you run out of
room (so that you don't end up too far away with Pluto). If possible, two or
more groups can do this part together.
Take your time, and let yourself imagine that you are on a
journey through an incredibly vast and empty solar system. Once you
reach the "end" of your journey, turn around and look for the Earth. Could
you find it if you didn't know where you had last placed it?
Have one of your group, or your instructor, walk at approximately the
speed of light for your model. Remember that in reality light travels at a
speed of 300,000 km/s, ie. if we could bend it in a circle, a light beam could
go around the Earth more than 7 times in one second! This should help give
a sense of how large a place our immediate neighborhood in space is in
reality.
Step 7. Using the fact that 1 mile = 1609 meters, also compute the scaled
distances in miles to the three outer-most planets in Table 2. Show your
work.
Scaled distance to Uranus =
miles.
Scaled distance to Neptune =
miles.
Scaled distance to Pluto =
miles.
-6-
Step 8. Show your calculations below to convert the actual distance to
Alpha Centauri (the nearest star) into miles. (Recall from Exercise 3 of the
Pre-lab Exercises that Alpha Centauri is 4.3 light-years away.)
Actual distance to Alpha Centauri =
miles.
Now, how far away is Alpha Centauri in your model? Look on the web
page below the speed of light.
Scaled distance to Alpha Centauri =
miles.
For reference, the distance from San Francisco to New York City is about
2500 miles.
-7-
Table 2. Scale Model "Solar System"
Actual
Actual
Scaled
Scaled
Measured
Diameter Distance Diameter Distance to Diameter
from
of Planet
Planet
of Selected
the Sun
Object
(km)
(cm)
(m)
(cm)
(106 km)
Sun
1,392,000
0
Mercury
4,878
57.9
Venus
12,102
108
Earth
12,756
149
Mars
6,794
228
Jupiter
142,984
778
Saturn
120,536
1427
Uranus
51,118
2870
Neptune
49,528
4497
Pluto
2,246
5914
Comments
(What objects did
you use and how
well did they match
the required scaled
size?)
0.00
Show all scaled diameters and distances to only three significant digits!
-8-
Name: __________________
Lab Partner: __________________
Pre-lab Exercises: Scaling and the Solar System
Show all of your work as well as the answers below. If you need extra
space, use the reverse side, or add scratch paper and staple it to the pre-lab
sheets.
1. Round the following numbers to three significant digits and convert
them to scientific notation:
160 =
1009 =
1,100,912 =
1,040,306,000,716,000 =
0.017309 =
0.00010145 =
123,699 =
0.0000000045682 =
2. (a) Since one mile is equal to 1.609 kilometers, how far away is the Sun in
kilometers if the average Earth-Sun distance is 93,000,000 miles? Note that
this distance (in any units) is defined to be one Astronomical Unit (1 A.U.).
(b) How many cm are in one A.U.?
(c) Imagine that you have just discovered Planet X, orbiting the Sun at a
distance of 500,000,000 kilometers. How many A.U.'s from the Sun is
Planet X? Round off your answer to two significant digits (i.e., 2.4).
-9-
3. One light-year is equal to the distance that light travels in one year.
Since light travels at a speed of 300,000 km/s, this is no small distance!
Using this information, and the facts that there are 60 seconds per
minute, 60 minutes in an hour, 24 hours in a day, and 365 days in a year,
determine the distance to the nearest star system (Alpha Centauri) in
kilometers. By the way, Alpha Centauri is 4.3 light-years away.
4. Using the given distances and diameters of objects in the solar system,
complete Table 1 of the lab. Each object in the table is listed together with
its actual diameter and actual distance from the Sun.
Obtain the Relative Diameter by dividing the diameter, D, of the
object by the diameter of the Earth. Similarly, calculate the Relative
Distance in A.U.'s by dividing the Distance from the Sun for the object by
the Earth's distance from the Sun. Recall that 1 A.U. is the average EarthSun distance. Also note the following:
1 km = 1000 m = 100,000 cm
1 m = 100 cm
-10-
Table 1. Planetary Data
Diameter
(km)
Distance
from the
Sun
(106 km)
Sun
1,392,000
0
Mercury
4,878
57.9
Venus
12,102
108
Earth
12,756
149
Mars
6,794
228
Jupiter
142,984
778
Saturn
120,536
1427
Uranus
51,118
2870
Neptune
49,528
4497
Pluto
2,246
5914
Relative
Diameter
(D/DEarth)
Relative
Distance in
A.U.'s
0.0
1.0
1.0
Show all relative diameters and distances to only two significant digits!
-11-