Download Ch 1 Linear Functions, Equations and Inequalities

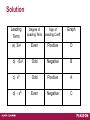
Higher-Degree Polynomial
Functions and Graphs
Ernesto Diaz
Professor of Mathematics
Copyright © 2011 Pearson Education, Inc.
Slide 1.4-1
Section 4.1
Polynomial
Functions and
Modeling
Copyright ©2013, 2009, 2006, 2005 Pearson Education, Inc.
Objectives

Determine the behavior of the graph of a
polynomial
function using the leading-term test.
 Factor polynomial functions and find the zeros and
their multiplicities.
 Use a graphing calculator to graph a polynomial
function and find its real-number zeros.
 Solve applied problems using polynomial models;
fit linear, quadratic, power, cubic, and quartic
polynomial functions to data.
Polynomial Function
A polynomial function P is given by
P( x )  an x n  an1x n1  an2 x n2  ...  a1x  a0,
where the coefficients an, an - 1, …, a1, a0 are real numbers
and the exponents are whole numbers.
Quadratic Function
Cubic Function
Examples of Polynomial Functions
Examples of Nonpolynomial Functions
Polynomial Functions
The graph of a polynomial function is continuous and
smooth. The domain of a polynomial function is the
set of all real numbers.
The Leading-Term Test
Example
Using the leading term-test, match each of the
following functions with one of the graphs AD,
which follow.
f ( x)  3x 4  2 x 3  3
a)
b)
f ( x)  x5  14 x  1
c)
f ( x)  5 x 3  x 2  4 x  2
f ( x)   x 6  x 5  4 x 3
d)
Graphs
a. f ( x)  3x 4  2 x3  3
b. f ( x)  5 x3  x 2  4 x  2
c. f ( x)  x5  14 x  1
d. f ( x)   x 6  x5  4 x3
Solution
Leading
Term
Degree of
Leading Term
Sign of
Leading Coeff.
Graph
a) 3x4
Even
Positive
D
b) 5x3
Odd
Negative
B
c) x5
Odd
Positive
A
d) x6
Even
Negative
C
Graphs
f ( x)  5 x 3  x 2  4 x  2
f ( x)  x5  14 x  1
f ( x)   x  x  4 x
6
5
3
f ( x)  3x 4  2 x 3  3
Finding Zeros of Factored Polynomial
Functions
If c is a real zero of a function (that is, f(c) = 0), then
(c, 0) is an x-intercept of the graph of the function.
Example
Find the zeros of f ( x)  5( x  1)( x  1)( x  1)( x  2)
 5( x  1)3 ( x  2).
To solve the equation f(x) = 0, we use the principle of
zero products,
solving x  1 = 0
and x + 2 = 0.
The zeros of f(x) are 1 and 2.
See graph on right.
Even and Odd Multiplicity
If (x  c)k, k  1, is a factor of a polynomial function
P(x) and (x  c)k + 1 is not a factor and:
 k is odd, then the graph crosses the x-axis at (c, 0);
 k is even, then the graph is tangent to the x-axis at
(c, 0).
Example
Find the zeros of f(x) = x3 – 2x2 – 9x + 18.
Solution We factor by grouping.
f(x) = x3 – 2x2 – 9x + 18 = x2(x – 2) – 9(x – 2).
 ( x  2)( x 2  9)
 ( x  2)( x  3)( x  3)
By the principle of zero products, the
solutions of the equation f(x) = 0, are 2, –3,
and 3.
Example
Find the zeros of f(x) = x4 + 8x2 – 33.
We factor as follows:
f(x) = x4 + 8x2 – 33 = (x2 + 11)(x2 – 3).
Solve the equation f(x) = 0 to determine the zeros.
We use the principle of zero products.
( x 2  11)( x 2  3)  0
x 2  11  0
x 2  11
or
x2  3  0
or
x2  3
x   11 or
x  i 11
x2   3
Example
Find the zeros of f(x) = 0.2x3 – 1.5x2 – 0.3x + 2.
Approximate the zeros to three decimal places.
Solution Use a graphing calculator to create a
graph. Look for points where the graph crosses the
x-axis. We use the ZERO feature to find them.
–10
10
The zeros are approximately –1.164, 1,142, and
7.523.
Example
The polynomial function
M (t )  0.5t 4  3.45t 3  96.65t 2  347.7t
can be used to estimate the number of milligrams of
the pain relief medication ibuprofen in the
bloodstream t hours after 400 mg of the medication
has been taken. Find the number of milligrams in the
bloodstream at
t = 0, 0.5, 1, 1.5, and so on, up to 6 hr. Round the
function values to the nearest tenth.
Solution
Using a calculator, we compute the function values.
Example-continued
Using a calculator, we compute the function values.
M (0)  0
M (3.5)  255.9
M (0.5)  150.2 M (4)  193.2
M (1)  255
M (4.5)  126.9
M (1.5)  318.3 M (5)  66
M (2)  344.4
M (5.5)  20.2
M (2.5)  338.6 M (6)  0
M (3)  306.9