Download Chapter 7 Similarity

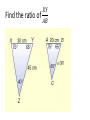
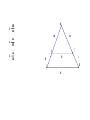
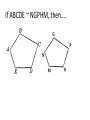
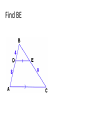
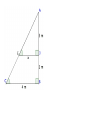
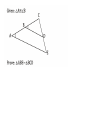
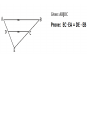
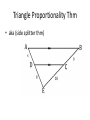
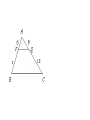
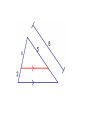
Chapter 7
Similarity
Definition: Ratio
• A quotient of two
𝑎
integers
𝑏
such that b≠0
• (must be reduced to lowest terms)
Find the ratio of
𝑋𝑌
𝐴𝐵
1.
2.
3.
A
AB
AD
14
AC
12
BE
CD
ED
E
B
8
10
7
D
C
24
• The angles of a pentagon are in ratio 4:2:5:5:2,
find the measure of each angle
4x+2x+5x+5x+2x = 540
18x
= 540
x
= 30
120, 60, 150, 150, 60
Definition: Proportion
• Two ratios set equal
•
𝑎
𝑏
𝑐
𝑑
= or a:b=c:d
Identify the means and extremes:
•
6
𝑥
=
9
14
• Find the third term of a proportion if 4, 9, and
15 are the first, second and fourth term
respectively.
4
9
=
𝑥
15
Definition: Geometric Mean
• A proportion in which the second and third
terms are equal
4
𝑥
=
𝑥
15
• Find the geometric mean between 5 and 28.
• 18 is the geometric mean between 7 and what
number?
Properties of Proportions:
• If
𝑎
𝑏
𝑐
𝑑
= , then:
a) ad = bc
b)
c)
d)
𝑎
=
𝑐
𝑏
=
𝑎
𝑎+𝑏
𝑏
𝑏
𝑑
𝑑
𝑐
=
(Means-Extremes Theorem)
( Interchanging property)
(Flipping property)
𝑐+𝑑
𝑑
(Denominator adding property)
Definition: Similar Polygons
• Two polygons are similar iff,
1) Corresponding angles are congruent
2) Corresponding sides are in proportion
If ABCDE ~ NGPHM, then….
Ways to prove triangles similar:
• 1) AA~ theorem
• 2) SSS~ theorem
• 3) SAS~ theorem
AA~ theorem
• If two angles of one triangle are congruent to
corresponding angles of another triangle, then
the triangles are similar.
Find BE
How tall is the tree?
• Given:
• Prove:
BC // DE
∆ABC ~ ∆ADE
Triangle Proportionality Thm
• aka (side splitter thm)
Triangle Angle Bisector Thm