* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Angles
History of trigonometry wikipedia , lookup
System of polynomial equations wikipedia , lookup
Perceived visual angle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Euler angles wikipedia , lookup
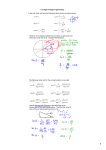
Monday: Bellwork Jason just transferred $59 out of his bank account. As a result, the account now has $223 left in it. How much money was in the account before the transfer? No Calculator until TESTING!!! Make a new section in your notes: Geometry Solving Problems with Angles-Notes 7. G.5 Use facts about supplementary, complementary, vertical, and adjacent angles in a multi‐step problem to write and solve simple equations for an unknown angle in a figure. Introduction The angle in RED is named ∠AOF The box shows that the angle is exactly 90° which is called a Right Angle (∠AOF) The line in GREEN is named 𝐵𝐸 An Acute Angle measures less than 90° (∠EOD) An Obtuse Angle measure more than 90° (∠BOD) A Straight Angle is a straight line. 𝐵𝐸 is equal to 180° Definitions and Examples Congruent- have the same angle measure Example: ∠AOF and ∠DOC are congruent Question: What is the measure of ∠DOC =_________ Adjacent- two angles that share a side (they TOUCH) Example: ∠FOE and ∠EOD share the side 𝑂𝐸 Question: Using what you know about right angles, what is the measure of ∠FOE =_________ Vertical Angles (opposite angles)- non-adjacent (they do not touch) angles that form from intersecting lines. They are congruent. Example: 𝐵𝐸 and 𝐴𝐷 intersect to form ∠AOB and ∠EOD Question: What is the measure of ∠AOB =_________ Definitions and Examples Complementary Angles- two angles whose measures add up to 90° (they do NOT have to be adjacent) Example: ∠AOB and ∠________ are complementary (adjacent) Example: ∠AOB and ∠________ are complementary (non-adjacent) Supplementary Angles- two angles whose measures add to 180° (they do NOT have to be adjacent) Example: ∠𝐵𝑂𝐷 and ∠__________ are supplementary (adjacent) Example: ∠COD and ∠________ are supplementary (non-adjacent) Finding Angle Measures ∠AOB=_________ ∠AOF=_________ ∠BOC=_________ ∠BOD=_________ ∠COD=_________ ∠FOB=_________ ∠FOE=_________ ∠EOA=_________ ∠EOC=_________ Using Equations to Find Angle Measures GUIDED EXAMPLE! Using Equations to Find Angle Measures GUIDED EXAMPLE! Using Equations to Find Angle Measures GUIDED EXAMPLE! Using Equations to Find Angle Measures GUIDED EXAMPLE! Using Equations to Find Angle Measures: Try this one on your own! Using Equations to Find Angle Measures: GUIDED EXAMPLE! Using Equations to Find Angle Measures: GUIDED EXAMPLE! Using Equations to Find Angle Measures: GUIDED EXAMPLE! Using Equations to Find Angle Measures: GUIDED EXAMPLE! Using Equations to Find Angle Measures: Try this one on your own! Extra Examples: Finish for Homework!! Tuesday: Bellwork Abe runs his own baking company. This morning, Abe's workers baked 455 cherry pies. They also baked some more after lunch. In total, they baked 744 cherry pies. How many cherry pies did Abe's workers bake after lunch? Solving Problems with Angles-Activity 7. G.5 Use facts about supplementary, complementary, vertical, and adjacent angles in a multi‐step problem to write and solve simple equations for an unknown angle in a figure. Building Block Task Cards You will be given a basic questions to start with Each question after builds on the previous question and answer If all building block task cards are complete, the final question is a multi-step question You will work in groups of 2-3 start with 1 card get answer checked If correct, get next card If incorrect, make corrections Wednesday: Bellwork 34 dogs participated in a dog show. The participation fee for each dog is $97. Find the amount collected for the participation fee. Solving Problems with Angles-Practice 7. G.5 Use facts about supplementary, complementary, vertical, and adjacent angles in a multi‐step problem to write and solve simple equations for an unknown angle in a figure. Independent Practice Work Independently to answer questions. If finished, you may get your sheet checked! Thursday: Half Day Solving Problems with Angles-Practice 7. G.5 Use facts about supplementary, complementary, vertical, and adjacent angles in a multi‐step problem to write and solve simple equations for an unknown angle in a figure. Friday: Bellwork Breanna has 378 pennies in a jar. If she divides them into stacks of 9, how many stacks does she have? Solving Problems with Angles-Practice 7. G.2. Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. Introduction: http://study.com/academy/lesson/measuring-the-angles-of-triangles-180-degrees.html Side Lengths: When you have the 3 side lengths of a triangle, there is only 1 triangle that can be formed The Third-Side Rule- The third side of a triangle must be smaller than the sum of the other two sides and must be greater than the difference between the other two sides. Example: Imagine you have a triangle with one side length of 10 and another side length of 4. What must be true about the third side? Side Lengths: Examples Can you make a triangle with the following side lengths? 1. 3 , 5, 8 yes no 2. 2, 3, 4 yes no why?__________________________ 3. 4, 4, 6 yes no why?__________________________ 4. 10, 15, 2 yes no why?__________________________ why?__________________________ Side Lengths: Challenge Angles: When you have 3 angles of a triangle, more than 1 triangle can be made: The sum of the interior or a triangle must equal 180° Does Makes a Triangle: Does NOT Make a Triangle: 30° , 60° , 90° 60° , 60° , 90° 30 + 60 + 90 =180° 60 + 60 + 90 = 210 Angles: Examples Can you make a triangle with the following angles? 1. 10° , 50° , 120° yes no 2. 110° , 80° , 10° yes no why?__________________________ 3. 18° , 101° , 61° yes no why?__________________________ 4. 66° , 53° , 78° yes no why?__________________________ why?__________________________ Angles: Challenge Extra Examples: Finish for Homework!!