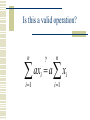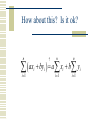Download Chapter 3

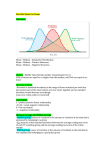
Chapter 3
Descriptive Statistics
Numerical Methods
Our goal? Numbers to help us
answer simple questions.
 What is a typical value?
 How variable are the data?
 How extreme is a particular value?
 Given data on two variables, how closely do
they move together?
Measures of Central Tendency
Here are three ways to identify a “typical”
observation
 Mean – the arithmetic average
 Median – the middlemost value
 Mode – the most common value
There are formulas, but . . .
One confusing thing about the formulas
is all the notation they use. To explain
why we need the notation, and why
you need to know it, let me remind you
of an important distinction . . .
Population vs. Sample
 A population is the set of all data that
characterize some phenomenon, and a
number computed from population data is
called a parameter.
 A sample is a subset of a population, and a
number computed from sample data is called
a statistic.
An Example
 Population - All registered voters.
 Parameter – The fraction of all registered
voters who prefer John McCain to Hillary
Clinton.
 Sample – 2500 voters surveyed by Gallup.
 Statistic – The fraction of voters in the poll
who prefer McCain to Clinton.
Another Example
 Population - All Duracell AA batteries.
 Parameter – The average lifetime of all
Duracell AA batteries in a particular toy.
 Sample – A hundred batteries being tested by
the manufacturer.
 Statistic – The average lifetime of the 100
tested batteries in the particular toy.
Why is the distinction
important?
 Sample statistics are very different from population
parameters. Parameters are fixed numbers. Before
the sample is drawn, statistics depend on the
elements that may be selected, and are random.
 Once a sample is drawn, the numbers themselves
are likely to be different; that is 48% of the
population but 51% of the sample may prefer
Clinton.
 Therefore, our notation must clearly distinguish
sample statistics from population parameters.
Now let us return . . .
To those measures of central tendency.
The Sample Mean
 The sample mean is the
arithmetic mean of
some sample data.
 The notation for a
sample mean is X-bar.
 The notation for
sample size is a lower
case n.
n
X
x
i 1
n
i
The Population Mean
 The population mean is
the arithmetic mean of
some population data.
 The notation for a
population mean is the
Greek letter mu.
 The notation for
population size is an
upper case N.
N

x
i 1
N
i
And THIS is the summation
operator
Here it is just telling us to add the
observations.
n
x
i 1
i
 x1  x2  x3
 xn
Don’t be intimidated by the
summation operator
 It is just shorthand; it saves space.
 The summation operator is just the Greek
letter Sigma.
 Sigma is Greek for S, and S stands for Sum.
 S for Sum, meaning “add them all up.”
Formulas with summation
operators confuse you?
 Consult Anderson, Sweeny, and Williams
Appendix C, and memorize the rules listed
there, or
 Do what I do, which is figure it out as you go
along . For example . . .
Is this a valid operation?
n
?
n
ax

a
x
 i  i
i 1
i 1
Just undo the shorthand to see!
n
 ax
 ax1  ax2  ax3 
axn
a  xi  a  x1  x2  x3 
xn 
i 1
i
n
i
n
So
 ax
i 1
i
n
a  xi
i
How about this? Is it ok?
n
?
n
n
  ax  by   a x  b y
i 1
i
i
i 1
i
i 1
i
Undo the shorthand to check
n
  ax  by   ax  by
i 1
i
i
n
n
i 1
i 1
1
1
 ax2  by2  ax3  by3
a  xi  b yi  a  x1  x2  x3
n
So, yes,
n
xn   b  y1  y2  y3
n
  ax  by   a x  b y
i 1
i
i
i 1
i
 axn  byn
i 1
i
yn 
Let’s go back to our formulas
 Suppose you are given the following data
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
Sample or population data?
 It depends on the context. Suppose this data came
from asking 13 people the number of computer
games they own.


If you are investigating the number of games owned by
these particular 13 people, then this is population data
If you are investigating the number of games owned by a
larger group, and these 13 people are members of that
group, then this is sample data.
 In homework problems, the default is sample data.
The mean in this example
n
X 
x
i 1
i
n
2  3  3  4  6  7  8  11  12  13  15  16  17
X 
9
13
The median in this example
 Since the median is the middlemost
observation, one way to find it is to order the
observations and throw away observations
one at a time from each end, until one is left
in the middle – in this case, 8.
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
2 , 3 , 3 , 4 , 6 , 7 , 8, 11, 12 , 13 , 15 , 16 , 17
Suppose you have an even
number of observations!
 In that case, you will be left with two
numbers in the middle when you have
finished eliminating numbers from both the
top and bottom.
 The median is found by adding those two
numbers and dividing by two.
The mode in this example
 Here is our data. Note that the only
observation that appears twice is “3” making
it the mode, or most common observation.
 But 3 is not a very typical observation, which
is why the mode is hardly ever used.
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
Mean vs. Median
 In 1983, the average starting salary of
Rhetoric and Communications majors at the
University of Virginia was approximately
$35,000 a year, far more than that of other
majors in the college of Arts and Science.
 Can you guess why?
Here is your answer!
 Ralph Sampson, a
Rhetoric and
Communications
major, was the first
pick in the NBA draft.
The Houston Rockets
paid him $2,000,000 a
year.
Robust Statistics
 A statistic is said to be robust if it is not
dramatically affected by a small number of
extreme observations.
 The median is robust, the mean is not.
 Therefore the median is usually a better
indication of a “typical value.”
How the mean and median
differ
 If a distribution is not symmetric . . .
 And there are a handful of extremely large or
small values . . .
 The mean will be pulled in the direction of
the extreme values.
 The Ralph Sampson story illustrates the
problem.
Look at the income distribution
in the USA in 1992
Asymmetric, skewed to the
right
 The median income is marked on the graph,
at about $22,000 a year.
 The mean is not reported, but it appears to be
about $30,000 a year.
Many people use statistics the
way a drunk uses a lamp post
 For support . . .
 Not for Illumination.
And they play games with the
mean and median
 An incumbent politician will boast of how
well the economy is doing, and use mean
income numbers as evidence.
 The challenger will complain of how badly
the economy is doing, and use median
income numbers as evidence.
 Confusing voters.
Measures of Variability
 Range
 Interquartile Range
 Variance
 Standard Deviation
 Coefficient of Variation
The Range
 The Range of a data set is just the difference
between the biggest and smallest
observation.
 The Range is easy to compute, but it is not
robust, and therefore may be misleading.
 As in: “Starting salaries for Rhetoric and
Communications majors range from $18,000
to $2,000,000 a year.”
An Example
 Lets use the earlier data to illustrate.
2, 3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
The Range is 17  2  15
Interquartile Range (IQR)
 This is the spread of the middle 50% of the
observations.
 It is defined as Q3 – Q1
 Q3 is the third quartile, or 75th percentile. 75% of
all observations are smaller than Q3.
 Q1 is the first quartile, or 25th percentile. 25% of
all observations are smaller than Q1.
 (Q2 is the second quartile, or median.)
How do you find quartiles?
 Basically, to find Q3, the 75th percentile,
order the data and throw away 3 observations
from the bottom for every one from the top.
Here, Q3 is 13.
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
2 , 3 , 3, 4 , 6 , 7 , 8 , 11, 12 ,13, 15, 16 , 17
Q1 works the same way
 To find Q1, the 25th percentile, order the data
and throw away 1 observation from the
bottom for every 3 from the top. Here Q1 is
4, so IQR = Q3 - Q1= 13 – 4 = 9.
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
2 , 3 , 3, 4, 6 , 7 , 8 , 11, 12 , 13 , 15, 16 , 17
I cheated a bit to make it simple
 With 13 observations, eliminating
observations in this way leaves you with just
one observation remaining.
 If the number of observations you have is not
equal to 4n+1 for some n, there will be two,
three, or four observations remaining.
 Then you must round or interpolate.
A, S, & W propose this solution
 Arrange data in ascending
order.
 Compute i, where p is the
percentile you seek and n is
the sample size.
 If i is an integer, average the
ith and i+1st observations.
 If i is not integer, round up.
 p 
i
n

 100 
An Example finding Q3





Here p = 75, n = 6.
Which gives i = 4.5.
Which is not integer.
So round up to 5.
The 5th observation is
9, so Q3 = 9.
2, 3, 6, 7, 9, 10
 75 
i
 6  4.5
 100 
An Example finding Q1




Here p = 25, n=8
Which gives i = 2.
Which IS an integer.
So average the second
and third observations.
 To get (5+6)/2 = 5.5
 So Q1 = 5.5
2, 5, 6, 6, 7, 8, 9, 10
 25 
i
8  2
 100 
But this is an arbitrary
convention
 Minitab uses a different rule.
 In our first example, where we got Q3 = 9,
Minitab gets Q3 = 9.25.
 In our second example, where we got Q1 =
5.5, Minitab gets Q1 = 5.25.
Variance of a Population
 The variance is the average
size of a squared deviation
about the mean.
 Lower-case sigma squared
is population variance.
 Note the use of mu and N in
the formula: all these are
population parameters.
N
 
2
 x   
i 1
i
N
2
Variance of a Sample
 Lower-case s-squared
denotes sample variance.
 Note the use of X-bar and n
in the formula: these are
sample statistics.
 Also note the funky
denominator, n-1, where
you would expect to see n.
n
s 
2
x  x 
i 1
i
n 1
2
Why use n-1 with sample data?
 A sophisticated explanation is coming in
Chapter 7, but think of it as a fudge factor.
 Having to compute squared deviations
around the sample mean instead of the true
population mean makes the numerator too
small.
 Dividing by n-1 corrects for this.
Example of the Calculation
 The heart of the calculation is evaluating the
numerator. Here is our example. Remember,
the mean is 9.
2,3, 3, 4, 6, 7, 8, 11, 12, 13, 15, 16, 17
 x
n
i
i 1
x
 x
n
i 1
i

2
  2  9  3  9  3  9
x
2

2
 49  36  36 
2
2
 338
Finishing the Variance
calculation
 Given the sum of
squared deviations
from the mean, the
calculation is as
follows:


Divide by n-1 for
sample data.
Divide by N for
population data.
n
s 
2
 x  x 
i
i 1
n 1
N
 
2
2
338

 28.1667
12
 x   
i 1
i
N
2
338

 26
13
The Standard Deviation
 The variance measures variability in
nonsense units; in this case, number of s 
computer games squared.
s
 To correct this, we introduce the
standard deviation, which is just the
square root of the variance.
 The standard deviation can be thought

of as the size of a typical deviation from

the mean.
s2
28.1667  5.31
2
26  5.099
Coefficient of Variation
 Seldom used in this course.
 Answers: “The standard
deviation is what percent
of the average?”
 Why is this useful?


An inch more or less in the
height of a skyscraper is
meaningless.
An inch more or less in the
length of your nose is a big
deal.
coefficient of variation 
s
100
x
s 5.31100

 59
x
9
Can you show us a use for the
standard deviation?
 Many real world data sets have an approximate bell
shape, as you no doubt have been told.
The Famous Bell Curve
Otherwise known as the Normal Distribution
C3
0.2
0.1
0.0
0
5
C2
10
A Rule for such variables
 68% of all observations are found within one
standard deviation of the mean.
 95.5% of all observations are found within two
standard deviations of the mean.
 99.7% of all observations are found within three
standard deviations of the mean.
 So any observation more than 2s from the mean is
unusual, and one more than 3s from the mean is
very unusual.
The z-Score
 This measures how many standard
deviations above or below the
mean a particular observation is.
 Positive values are above the
mean, negative ones below.
 Any z greater than 2 in absolute
value is a mild outlier.
 Any z greater than 3 in absolute
value is a substantial outlier.
xi  x
zi 
s
Why should we care about
outliers?
 Depends on the circumstances, but outliers
often require investigation.



An outlier may signal a data entry error!
An outlier may identify a particularly poor
outcome that needs to be corrected.
An outlier may identify a particularly good
outcome that needs to be emulated.
Measures of Association
between two variables
 Often we want to know whether variables are
positively or negatively associated, and if so,
how strong the association is.
 Some examples will illustrate what I mean.
Positive association
No association
Negative association
No linear association, but . . .
Covariance
 A measure of the
degree of linear
N
association.
 xi   x   yi   y 

 It is an “average size”  xy  i 1
N
of a cross product.
n
 First formula is the
 xi  x  yi  y 

population covariance.
sxy  i 1
n 1
 Second formula is the
sample covariance.
Why this cross product?
 xi  x  yi  y 
 When x and y are simultaneously bigger than their means,
both terms are positive, contributing a positive term to the
sum.
 When x and y are both simultaneously smaller than their
means, both terms are negative, once again contributing a
positive term to the sum.
 Positively related variables will have many + terms in the
sum.
Conversely. . .
 xi  x  yi  y 
 If a big x and small y are paired, the first term is
positive,while the second is negative, contributing a negative
term to the sum.
 If a small x and big y are paired, the first term is
negative,while the second is positive, contributing a negative
term to the sum.
 Negatively related variables will have many negative terms
in the sum.
And if x and y are unrelated
 The sum will consist of offsetting positive
and negative terms.
 Therefore:



A positive covariance means positive association
A negative covariance means negative
association
A zero covariance means no (linear) association.
An example
 Here are some data: on casual
observation they seem positively
associated.
 First we need the mean of each of
the two variables.
 The mean of x is 16.
 The mean of y is 10.
X
Y
6
6
11
9
15
6
21
17
27
12
Computing the numerator
n
  x  x  y  y 
i 1
i
i
  6  16  6  10   11  16  9  10   15  16  6  10 
  21  16 17  10    27  16 12  10 
  10  4    5  1   1 4    5  7   11 2 
 40  5  4  35  22  106
Completing the calculation
 The numerator is the
same for both the
sample and population
covariance.
 The only difference is
in the denominator,
because of the n-1
divisor.
 x    y   
N
 xy 

i 1
i
x
i
N
106
 21.2
5
n
sxy 
  x  x  y  y 
i 1
i
i
n 1
106

 26.5
4
y
Hmmm . . .
 We can see that the relationship is positive
because the covariance is positive, but what
are we to make of 26.5? Is that big or small?
The Covariance is Flawed
 There are really TWO problems.


The covariance lacks a scale, so we have no way
to judge its size.
The covariance depends on units. Measuring x
and y in inches we’d get one answer. Someone
measuring x and y in centimeters would get a
different answer – even though the degree of
association is exactly the same!
Correlation is superior
 Top formula defines
the population
correlation.
 Bottom formula
defines the sample
correlation.
 Correlation is unit free
and always between –1
and +1.
 xy
 xy 
 x y
rxy 
sxy
sx s y
Interpreting the correlation
 A positive correlation implies a positive
association, and conversely, since the
correlation has the same sign as the
covariance.
 A zero correlation implies no linear
association.
 A correlation near one in absolute value is a
very strong relationship; one near zero, weak.
For Example . . .
Our second example . . .
Our third example . . .
Remember, correlation
measures linear association!
Returning to the example . . .
 Here is our data.
 To compute a correlation
coefficient, we need to first
compute standard deviations of
both X and Y.
X
Y
6
6
11
9
15
6
21
17
27
12
Standard deviation of X
n
  x  x    6  16   11  16 
2
2
2
i
i 1
 15  16    21  16    27  16 
2
2
2
 100  25  1  25  121  272
sx 
x 
n
  xi  x 
 n  1 
2
272 4  8.246
i 1
N
  xi   x 
i 1
2
N  272 5  7.376
Standard deviation of Y
n
  y  y    6  10    9  10 
2
2
2
i
i 1
  6  10   17  10   12  10 
2
2
2
 16  1  16  49  4  86
n
sy 
  yi  y 
y 
 y   
 n  1 
2
86 4  4.637
i 1
N
i 1
i
y
2
N  86 5  4.147
Completing the computation
sxy
26.5
rxy 

 .693
sx s y  8.246  4.637 
 xy
21.2
 xy 

 .693
 x y  7.376  4.147 
A few comments
 It is not an accident that the numbers are the
same. The only difference in the population
and sample formulas is in divisors: n-1 vs. N.
 Those different divisors appear in both
numerator and denominator and cancel out.
 The conclusion, a correlation of .693, implies
a moderately strong positive association
Grouped Data
 Here is a problem using
grouped data.
 Original observations lost
though grouping.
 Treat this as follows:




4 observations of 5,
7 observations of 10,
9 observations of 15, and
5 observations of 20.
Class
Midpoint
Freq
3-7
5
4
8-12
10
7
13-17
15
9
18-22
20
5
ASW, #53, p. 119
25
Existing formulas work but are
tedious!
n
X
x
i 1
n
i
4 times

55
7 times
 10  10 
9 times
 15  15 
25
n
X
x
i 1
n
i
325

 13
25
5 times
 20  20 
This is why one multiplies
 The top formula is for
sample data.
 The bottom formula is
for population data.
 M sub-i is midpoint of
the ith category.
 f sub-i is the frequency
or count of the ith
category.
fM

X
i


n
fi M i
N
i
So the calculation works this
way
 Just take each midpoint
 Multiply by the
corresponding
frequency.
 Add up the products,
and you have the
numerator.
Midpoint
Frequency
fiMi
5
4
20
10
7
70
15
9
135
20
5
100
fM
i
i

325
The last step
 Just the same for the
population mean.
 Warning: the sample
size is 25 (the sum of
the frequencies), not 4
(the number of
categories).
fM

X
i
i
n
325
X
 13
25
Variance formulas for grouped
data
 Same rationale as
formulas for the mean;
while previous formulas
work, these are easier,
because multiplication
replaces addition.
 Top formula is for sample
data; bottom for
population data.
s
2

f M


i
 x
i
2
n 1
2
f M


i
i
N
 x 
2
Computing the numerator
Midpoint
Frequency
Mi  x 
2
fi  M i  x 
5
4
64
256
10
7
9
63
15
9
4
36
20
5
49
245

fi  M i  x  
2
600
2
Completing the calculation
 Calculation of the
numerator is identical
for both the population
and sample variance.
 Only difference is for
sample measure, divide
by n-1; population
measure divide by N.
s
2
f M


i
i
 x
2

n 1
600
 25
24
s  s2  5

2


fi  M i   
N
2
600

 24
25
   2  24  4.899
That is it for today!