* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download resistance
Survey
Document related concepts
Transcript
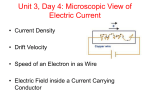
PHY 184 Spring 2007 Lecture 16 Title: Electric Current and Resistance 2/5/07 184 Lecture 16 1 Announcements Homework Set 4 is due tomorrow at 8:00 am. Midterm 1 will take place in class Thursday, February 8 • Will cover Chapters 16 - 19 • Homework Set 1 - 4 • You may bring one 8.5 x 11 inch sheet of equations, front and back, prepared any way you prefer • Bring a calculator • Bring a No. 2 pencil • Bring your MSU student ID card We will post Midterm 1 as Corrections Set 1 after the exam • You can re-do all the problems in the Exam • You will receive 30% credit for the problems you missed • To get credit, you must do all the problems in Corrections Set 1, not just the ones you missed 2/5/07 184 Lecture 16 2 Review Electric current i is the net charge passing a given point in a given time dq i dt The ampere is abbreviated as A and is given by 1C 1A 1s The current per unit area flowing through a conductor is the current density J If the current is constant and perpendicular to a surface, then and we can write an expression for the magnitude of the current density i J A 2/5/07 184 Lecture 16 3 Electron Drift Velocity In a conductor that is not carrying current, the conduction electrons move randomly. (thermal motion) When current flows through the conductor, the electrons have an additional coherent motion. (drift velocity, vd ) The magnitude of the velocity of random thermal motion is on the order of 106 m/s while the magnitude of the drift velocity is on the order of 10-4 m/s We can relate the current density J to the drift velocity vd of the moving electrons. 2/5/07 184 Lecture 16 4 Electron Drift Velocity (2) Consider a conductor with cross sectional area A and electric field E. Suppose that there are n electrons per unit volume. The negatively charged electrons will drift in a direction opposite to the electric field. We assume that all the electrons have the same drift velocity vd and that the current density J is uniform. In a time interval dt, each electron moves a distance vddt . The volume that will pass through area A is then Avd dt; the number of electrons is dn = nAvd dt . 2/5/07 184 Lecture 16 5 Electron Drift Velocity (3) Each electron has charge e so that the charge dq that flows through the area A in time dt is dq i nevd A dt So the current is … and the current density is i J nevd A The current density and the drift velocity are parallel vectors, pointing in opposite directions. As vectors, J nev d 2/5/07 184 Lecture 16 6 Electron Drift Velocity (4) Consider a wire carrying a current The physical current carriers are negatively charged electrons. These electrons are moving to the left in this drawing. However, the electric field, current density and current are directed to the right. Comments Electrons are negative charges! On top of the coherent motion the electrons have random (thermal) motion. 2/5/07 184 Lecture 16 7 Clicker Question The figure shows positive charge carriers that drift at a speed vd to the left. In what directions are J and E? A) J and E point to the right B) J points to the left, E to the right C) J points to the right, E to the left D) J and E point to the left 2/5/07 184 Lecture 16 8 Example - current through a wire (1) The current density in a cylindrical wire of radius R=2.0 mm is uniform across a cross section of the wire and has the value 2.0 105 A/m2. What is the current i through the outer portion of the wire between radial distances R/2 and R? J = current per unit area = di / dA 2/5/07 184 Lecture 16 R 9 Example - current through a wire (1) The current density in a cylindrical wire of radius R=2.0 mm is uniform across a cross section of the wire and has the value 2.0 105 A/m2. What is the current i through the outer portion of the wire between radial distances R/2 and R? J = current per unit area = di / dA R Area A’ (outer portion) Current through A’ 2/5/07 184 Lecture 16 10 Resistance and Resistivity Some materials conduct electricity better than others. If we apply a given voltage across a conductor, we get a large current. If we apply the same voltage across an insulator, we get very little current (ideal: none). The property of a material that describes its ability to conduct electric currents is called the resistivity, The property of a particular device or object that describes it ability to conduct electric currents is called the resistance, R Resistivity is a property of the material; resistance is a property of a particular object made from that material. 2/5/07 184 Lecture 16 11 Resistance and Resistivity (2) If we apply an electric potential difference V across a conductor and measure the resulting current i in the conductor, we define the resistance R of that conductor as V R i The unit of resistance is volt per ampere. In honor of George Simon Ohm (1789-1854) resistance has been given the unit ohm, 1V 1 1A 2/5/07 184 Lecture 16 12 Resistance and Resistivity (3) We will assume that the resistance of the device is uniform for all directions of the current; e.g., uniform metals. The resistance R of a conductor depends on the material from which the conductor is constructed as well as the geometry of the conductor First we discuss the effects of the material and then we will discuss the effects of geometry on resistance. 2/5/07 184 Lecture 16 13 Resistivity The conducting properties of a material are characterized in terms of its resistivity. We define the resistivity, , of a material by the ratio E J E: magnitude of the applied field J: magnitude of the current density The units of resistivity are V Vm m = m A A 2 m 2/5/07 184 Lecture 16 14 Typical Resistivities The resistivities of some representative conductors at 20° C are listed in the table below Material Silver Copper Gold Aluminum Nickel Mercury Resistivity ( m ) 1.5910-8 1.7210-8 2.4410-8 2.8210-8 6.8410-8 95.810-8 Resistivity ((-cm) ž cm ) 1.59 1.72 2.44 2.82 6.84 95.8 As you can see, typical values for the resistivity of metals used in wires are on the order of 10-8m. 2/5/07 184 Lecture 16 15 Resistance Knowing the resistivity of the material, we can then calculate the resistance of a conductor given its geometry. Derivation: Consider a homogeneous wire of length L and constant cross sectional area A. V i E and J L A … the resistance is R 2/5/07 V EL L i JA A 184 Lecture 16 16 Resistance and resistivity For a wire, L R A 2/5/07 184 Lecture 16 17 Clicker Question You have three cylindrical copper conductors. Rank them according to the current through them, the greatest first, when the same potential difference V is placed across their lengths. A: a, b, c B: a and c tie, then b C: b, a, c D: a and b tie, then c 2/5/07 184 Lecture 16 18 Clicker Question You have three cylindrical copper conductors. Rank them according to the current through them, the greatest first, when the same potential difference V is placed across their lengths. B: a and c tie, then b D: a and b tie, then c 2/5/07 184 Lecture 16 19 Example: Resistance of a Copper Wire Standard wires that electricians put into residential housing have fairly low resistance. Question: What is the resistance of a length of 100 m of standard 12gauge copper wire, typically used in household wiring for electrical outlets? Answer: The American Wire Gauge (AWG) size convention specifies wire cross sectional area on a logarithmic scale. A lower gauge number corresponds to a thicker wire. Every reduction by 3 gauges doubles the cross-sectional area. 2/5/07 184 Lecture 16 20 Example: Resistance of a Copper Wire (2) The formula to convert from the AWG size to the wire diameter is (36 AWG)/ 39 d 0.127 92 mm So a 12-gauge copper wire has a diameter of 2.05 mm Its cross sectional area is then A d 3.3 mm 1 4 2 2 Look up the resistivity of copper in the table … L 100 m -8 R (1.72 10 m) 0.52 -6 2 A 3.3 10 m 2/5/07 184 Lecture 16 21 Clicker Question A rectangular block of iron has dimensions 2.0cm x 2.0 cm x 10cm. A potential difference is to be applied to the block between parallel sides. What is the ratio of the resistances R(1)/R(2) of the block for the two arrangements (1) and (2). A) B) C) 2/5/07 (1) 2.0 cm 2.0 cm 184 Lecture 16 10 cm (2) 22 Clicker Question A rectangular block of iron has dimensions 2.0cm x 2.0 cm x 10cm. A potential difference is to be applied to the block between parallel sides. What is the ratio of the resistances R(1)/R(2) of the block for the two arrangements (1) and (2). A) (1) 2.0 cm 2.0 cm 10 cm (2) R1 L1 / A1 L1 A2 10 20 25 R2 L2 / A2 L2 A1 2 4 2/5/07 184 Lecture 16 23 Resistors In many electronics applications one needs a range of resistances in various parts of the circuits. For this purpose one can use commercially available resistors. Resistors are commonly made from carbon, inside a plastic cover with two wires sticking out at the two ends for electrical connection. The value of the resistance is indicated by four colorbands on the plastic capsule. The first two bands are numbers for the mantissa, the third is a power of ten, and the fourth is a tolerance for the range of values. 2/5/07 184 Lecture 16 24 Resistors (2) The number associated with the colors are: • • • • • • • • • • black = 0 brown = 1 red = 2 orange = 3 yellow = 4 green = 5 blue = 6 purple = 7 gray = 8 white = 9 For example, the single resistor shown here has colors (top to bottom) brown, green, brown and gold Using our table, we can see that the resistance is 15×101 = 150 with a tolerance of 5% In the tolerance band • gold means 5% • silver means 10% • no tolerance band means 20% 2/5/07 184 Lecture 16 25 Summary J nev d L R A 2/5/07 .. speed of an electron .. resistance to current 184 Lecture 16 26