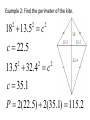* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Honors Geometry Section 4.5 (3) Trapezoids and Kites
Line (geometry) wikipedia , lookup
Rational trigonometry wikipedia , lookup
Multilateration wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of geometry wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Noether's theorem wikipedia , lookup
Four color theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Euler angles wikipedia , lookup
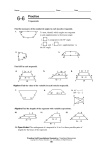
Honors Geometry Section 4.5 (3) Trapezoids and Kites Two special types of quadrilaterals that are NOT parallelograms are trapezoids and kites. A trapezoid is a quadrilateral with exactly one pair of opposite sides parallel. bases The sides that are parallel are called _______. The nonparallel sides are called ______. legs The angles at each end of a base are base angles called _____________. A midsegment of a trapezoid is the segment joining the midpoints of the two legs. Theorem The midsegment of a trapezoid is parallel to the bases and the length of the midsegment is equal to ½ the sum of the bases. AB // ED // FC FC 1 AB ED 2 2 FC AB ED An isosceles trapezoid is a trapezoid that has congruent legs. Theorem In an isosceles trapezoid, the base angles that share a common base are congruent. Note: For any trapezoid the angles that share a common leg are _____________. supplementary Theorem The diagonals of an isosceles trapezoid are congruent. Example 1: Find the value of x, y and z in this isosceles trapezoid. y 43 z 137 2(40 x 19) 4 x 16 8 x 31 80 x 38 12 x 47 68 x 85 x 85 1.25 68 A kite is a quadrilateral with two pairs of congruent adjacent sides and noncongruent opposite sides. Theorem The diagonals of a kite are perpendicular. Example 2: Find the perimeter of the kite. 18 13.5 c 2 2 2 c 22.5 13.5 32.4 c 2 2 2 c 35.1 P 2(22.5) 2(35.1) 115.2