* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download dist(i,s)+
Survey
Document related concepts
Transcript
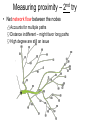
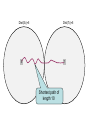
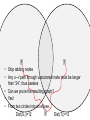
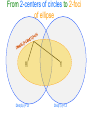
Measuring and Extracting Proximity in Complex Networks Emden Gansner, Yehuda Koren, Stephen North, Chris Volinsky AT&T Labs Research AT&T “Safe Harbor” The following contains "forward-looking statements" which are based on management's beliefs as well as on a number of assumptions concerning future events made by and information currently available to management. Readers are cautioned not to put undue reliance on such forward-looking statements, which are not a guarantee of performance and are subject to a number of uncertainties and other factors, many of which are outside AT&T's control, that could cause actual results to differ materially from such statements. For a more detailed description of the factors that could cause such a difference, please see AT&T's filings with the Securities and Exchange Commission. AT&T disclaims any intention or obligation to update or revise any forward-looking statements, whether as a result of new information, future events or otherwise. large social networks data source |V| |E| co-authors 438K 31M actor-actor 896K 1.1M phone calls 300M 1000M 200M 800M IM 18 node subgraph Proximity: 1.35e+01 Captured: 1.31e+01 (97%) Adam? Glenn? Emden? 95% of communication between… 5 node subgraph Proximity: 7.10e+00 Captured: 6.74e+00 (95%( Our goals • Measure proximity between nodes. • Explain proximity by extracting connection subgraphs that are readily visualized. What is proximity? • proximity [prox·im·i·ty || prɑk'sɪmətɪ /prɒ-]n. adjacency, nearness, closeness, vicinity • Network proximity is an elusive notion! • Let’s work by refining a series of definitions. Measuring proximity • Simplest approach – length of shortest path Easily visualized Measuring proximity • Simplest approach – length of shortest path Easily illustrated Disregards alternative paths Captures 56% Captures 98% Measuring proximity • Simplest approach – length of shortest path Easily visualized Disregards alternative paths Naïve calculation will be fooled by high degrees Example from a telephone call graph… Which pair is closer? Meaningful connection Suresh Shankar Random connection? Lefty Stephen • Both paths are 2-hops, about the same lengths • But when considering node-degrees… Measuring proximity – 2nd try • Net network flow between the nodes Accounts for multiple paths Distance indifferent – might favor long paths High degree are still an issue Measuring proximity – 3rd try • Delivered electric current (effective conductance) • Resistor network model Accounts for multiple paths Penalizes long paths • High degrees?? • Getting us closer… • “intuitive” Physical analogy is not perfect! 1V 0V edge weights conductance, inverse-resistance When is the electrical current analogy misleading? Significant connection Noise? What does current flow mean? When is the electric current analogy misleading? Significant connection Noise? • Same current flow in both cases! • Degree-1 nodes are neutral (attract no flow) • Degree-1 nodes are very common, due to incomplete information Augment network by a universal sink [Faloutsos, McCurley & Tomkins, KDD 2004] • Connect all nodes to a grounded universal sink (with 0V) • Tax each node - deliver portion of the flow to the sink No internal nodes of degree 1 (above problem solved) Penalizes long paths A new parameter to worry about: Which tax system? Constant tax? Proportional tax? Tax brackets? How much? • There is a worse problem… Universal sink and (non-)monotonicity Proximity • In our previous notions of proximity, adding nodes/edges to the network couldn’t decrease proximity • Hmmm…this “blind monotonicity” was part of their shortcoming… Network size Universal sink and (non-)monotonicity Proximity • For all previous measures, adding nodes/edges to the network couldn’t decrease proximity • With universal sink – no monotonicity: Larger network proximity tends to zero, sink attracts more flow • Even adding s—t paths can decrease proximity! Network size Universal sink and (non-)monotonicity • Problems with non-monotonicity: Proximity – Counter-intuitive and hard to use – Size bias makes proximity-comparison across different pairs completely unreliable – Impossible to explain (size-dependent) proximity using a connection subgraph Network size A random-walk perspective • Current-flow model has a direct r.w. interpretation • Reminder: We defined proximity by “delivered current” or “effective conductance” • The escape probability, Pesc(st), is the probability that a r.w. originating at s will reach t before visiting s again • Let Deg(s) be the number of r.w.’s originating at s • The effective conductance between s and t, is Pesc(st)*Deg(s) • “Dead end” paths have no influence on escape probability • Both graphs have the same escapeprobability from red to green Lower redgreen escape probability Higher redgreen escape probability In both cases higher effective conductance by Rayleigh’s Monotonicity Law Extending escape probability • The escape probability, Pesc(st), is the probability that a r.w. originating at s will reach t before visiting s again • The cycle-free escape probability, Pc.f.esc(st) is the probability that a r.w. originating at s will reach t without visiting any node more than once • Multiply by degree to get an absolute quantity (accounting for the number of "actually initiated" r.w.'s): The c.f. effective conductance between s and t is Pc.f.esc(st)*Deg(s) Higher redgreen c.f. escape probability Lower redgreen c.f. escape probability • The c.f. effective conductance is a good candidate proximity measure: Accounts for multiple paths Favors short paths Penalizes high-degree nodes Penalizes dead-end paths Parameter free Has the “right” monotonicity Accommodates edge directions Has a natural extension to multiple endpoints Computing c.f. escape probability • Unlike previous measures, exact computation is impossible Pc.f.esc (s t ) = prob( p) simple path p[ s t ] • Practically, we can estimate it extremely well • Probability of paths declines exponentially (e.g., 100th path is x106 less probable than the first one.) • Estimate using the most probable paths: Pc.f.esc (s t ) = highly probable simple path p[ s t ] prob( p) Finding k most probable paths • For an edge u-v of weight w(u,v), define its length w(u, v) l (u, v) = log deg(u ) deg(v) • • • • Edge lengths are positive Exp(-<length of path>) = Prob(path) Short path High-probable path Compute k shortest simple paths in O(k|E|log|E|) time [Katoh, Ibarki and Mine, 1982] • Stop searching when probability drops below “10-6” of first path Extracting and explaining proximity Extracting proximity • Cycle free effective conductance (CFEC) depends on the full graph • Find a small subgraph that captures the most proximity • A tradeoff between “size” and “captured proximity”, can be expressed in alternative ways: – Extract a subgraph with at most B nodes that captures maximal CFEC • Maybe with B+1 nodes we can capture much more??? – Extract a minimal-sized subgraph that captures at least P% of total CFEC • Maybe we can capture (P-1)% of total CFEC with a much smaller subgraph??? Extracting proximity • Find a small subgraph that captures most proximity • Achieve an efficient balance between “size” and “proximity” by maximizing the ratio: CFEC(s t ) subgraph • Larger α emphasize proximity larger subgraph – α=0 returns only the shortest path – α=∞ return all paths • Optionally, explicitly fix lower and upper bounds on subgraph size What solutions do we seek? • Overlapping paths delivering the most flow The path merger algorithm • We already have a collection of paths • Find the subset of the paths that maximizes CFEC(s t ) subgraph • Combine the selected paths into a “proximity subgraph” • Overlapping paths are cheaper to add • An NP-hard problem… Optimal algorithm • Scanning all subsets takes O(2k) time (can we do better?) • A branch-and-bound pruning significantly reduces running time • Huge deviations in path-quality make this approach effective e.g. often it is clear that the best-subset must contain first path(s) • Prematurely terminate exponential algorithm after scanning “too many” subsets Agglomerative algorithm • If optimal algorithm couldn’t finish, improve current result by an agglomerative algorithm • Iteratively, merge the two subsets that maximize the ratio • Record the best subset discovered Working with large graphs in external storage • Dealing with full graph is sometimes infeasible and usually unnecessary • Prior to running the algorithm, we construct a candidate graph in main memory • We begin by growing increasing neighborhoods around the endpoints S T Dist(S,i)=2 S Dist(T,i)=2 T Dist(S,i)=3 S Dist(T,i)=3 T Dist(S,i)=4 S Dist(T,i)=4 T Dist(S,i)=5 Dist(T,i)=5 S T Shortest path of length 10 Most probable path of length 10 was found No use for lowprobability paths... Paths longer than “24” unneeded! S Dist(S,i)=12 T Dist(T,i)=12 S T • Stop adding nodes • Any s—t path through unscanned node must be longer than “24”, thus useless • Can we prune the resulting graph? • Yes! • From two circles into an ellipse… Dist(S,i)=12 i Dist(T,i)=12 Pruning the candidate graph • We can safely prune a significant portion of the candidate graph • Use the fact: dist(i,s)+dist(i,t)>L all s—t paths going via i are longer than L • We ignore much less probable paths Paths longer than “24” are not interesting • Take only nodes within the ellipse defined by: dist(i,s)+dist(i,t)<24 From 2-centers of circles to 2-foci of ellipse S Dist(S,i)=12 T Dist(T,i)=12 Some statistics… Distribution of proximities in phone-call network Distribution of #hops in phone-call network Summary • Proposed cycle free effective conductance (CFEC) with a random walk interpretation to measure “proximity” in social networks and other ad-hoc networks • Described a way of approximating CFEC • Described a way of visualizing CFEC as a subgraph • Extended the method to external datasets • Showed empirical evidence for its utility Extensions • Study proximity in other kinds of networks. • Extend c.f. effective conductance to: – Multiple endpoints (already demonstrated) – Directed edges (future work – use k-shortest paths in a directed graph, alg. due to Hershberger et al ).