Download Theorem

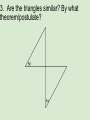
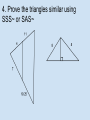
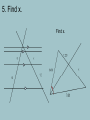
Chapter Six Review
By Mitch, Andrew,
Gwyne, Pietro
6.1 Similar Polygons
Vocabulary
similar: shapes with congruent corresponding angles and
proportional corresponding sides
scale factor: the ratio of the lengths between corresponding
sides (2:5, 6:13, 1:3)
Theorems
Similar Polygon Perimeters
If two polygons are similar, the ratio of their perimeters is the
same as the ratio of the lengths of their corresponding sides
6.2 Transformations and Dilations
Vocabulary
dilation: transformation with same angle measures and
proportional corresponding sides from original to image
scale factor: also called k, number coordinates are multiplied
for image- (kx, ky)
-If you move a figure onto another figure with a dilation, then
the figures are similar
-You can also combine dilations with
reflections, translations, and rotations!
6.3 Triangles Similar by AA~ Postulate
AA~ Postulate
If two angles of one triangle are congruent to two angles of a
different triangle, the triangles are similar.
6.4 Triangles Similar: SSS~, SAS~
SSS~ Theorem
If the corresponding sides of two triangles are proportional,
then the triangles are similar.
SAS~ Theorem
If two corresponding sides of a triangle are proportional and
the included angles are congruent, then the triangles are
similar.
6.5 Use Proportionality Theorems
Triangle Proportionality
Theorem
If lines 1 and 2 are
parallel, then
Side Splitter Theorem
If BD is and angle bisector of
<ABC, then a/x=b/y or
6.6 Similarity Transformations
Vocabulary
center of dilation: the fixed point around which a figure is
enlarged or reduced (dilated)
enlargement: if k>1 in (kx, ky)
reduction: if 0<k<1 in (kx, ky)
(It's kind of a boring chapter, people)
Quiz!
Small Triangle: a=10, b=6, c=9
Large Triangle: a=27, b=16.2, c=24.3
1.Are the triangles similar? If so, what is the scale factor from
the small triangle to the large triangle?
2. What are the transformations of the triangles?
3. Are the triangles similar? By what
theorem/postulate?
4. Prove the triangles similar using
SSS~ or SAS~
5. Find x.
Find x.
6. Draw a figure with the given vertices
using a scale factor of .5. Is the dilation
a reduction or an enlargement?
S(-4,2)
U(-2,4)
P(2,4)
E(4,2)
R(0,-3)
Multiple Choice
7. Are the triangles similar?
a) Yes, by AA~ Theorem
b) Yes, by SAS~ Theorem
c) Yes, by AAA~ Theorem
d) No, not similar
e) Yes, by AAS~ Theorem
f)None of the above
8. Another name for a dilation is a...
a) Change
b) Shrink
c) Similarity transformation
d) Glenn
Always, Sometimes, Never?
9. A rotation is a form of dilation.
10. Similar triangles are congruent.
12. Isosceles triangles are similar.