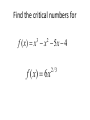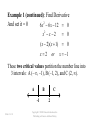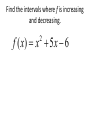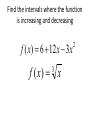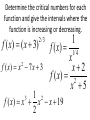Download 4.1 Increasing\decreasing, graphs and critical numbers

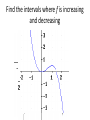
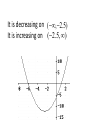
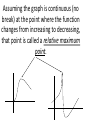
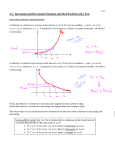
5.1 Increasing\decreasing, graphs
and critical numbers
A function is increasing when its graph
rises as it goes from left to right.
A function is decreasing when its graph
falls as it goes from left to right.
The inc\dec concept can be associated with
the slope of the tangent line.
The slope of the tan line is positive when
the function is increasing.
The slope of the tan line is and negative
when decreasing
On an interval on which f is defined
(a) if f ‘(x) > 0 for all x in an interval,
then f is increasing on the interval.
(b) if f ‘(x) < 0 for all x in an interval,
then f is decreasing on the interval.
(c) if f ‘(x) = 0 for all x in an interval
then f is constant on that interval.
Find the intervals where f is increasing
and decreasing
DEFINITION:
A critical value (or critical number) of a function f
is any number c in the domain of f for which the
tangent line at (c, f (c)) is horizontal or for which
the derivative does not exist.
That is, c is a critical value if f (c) exists and
f (c) = 0 or f (c) does not exist.
These are the x values where the function
could change from increasing to decreasing
or vice-versa.
Slide 2.1- 6
Copyright © 2008 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley
Find the critical numbers for
f ( x)  x  x  5 x  4
3
2
f ( x)  6 x
2/3
Steps For Finding Increasing and
Decreasing Intervals of a Function
1) Find the derivative
2) Find numbers that make the derivative equal to 0,
and find numbers that make it undefined. These are
the critical numbers.
3) Put the critical numbers and any x values where f is
undefined on a number line, dividing the number line
into sections.
4) Choose a number in each interval to test in the first
derivative. Make a note of the sign you get.
5) Intervals that have first derivatives that are positive,
are increasing, and intervals that have first
derivatives that are negative, are decreasing.
Example 1:
Find the increasing and
decreasing intervals for the
funtion given by
f ( x)  2 x  3x  12 x  12.
3
Slide 2.1- 9
2
Copyright © 2008 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley
Example 1 (continued): Find Derivative
And set it = 0
6x 2  6x  12  0
x2  x  2
(x  2)(x  1)
x2
or
 0
 0
x  1
These two critical values partition the number line into
3 intervals: A (– ∞, –1), B (–1, 2), and C (2, ∞).
A
B
-1
Slide 2.1- 10
C
2
Copyright © 2008 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley
Example 1 (continued):
3rd analyze the sign of f (x) in each interval.
Interval
A
C
B
-1
x
2
Test Value
x = –2
x=0
x=4
Sign of
f (x)
+
–
+
Result
Slide 2.1- 11
f is increasing f is decreasing on
on (–∞, –1]
[–1, 2]
Copyright © 2008 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley
f is increasing
on [2, ∞)
Find the intervals where f is increasing
and decreasing.
f ( x)  x  5 x  6
2
Since f ’(x) = 2x+5 it follows that
f is increasing when 2x+5>0 or
when x>-2.5 which is the interval
(2.5, )
It is decreasing on (,2.5)
It is increasing on (2.5, )
Find the intervals where the function
is increasing and decreasing
f ( x)  6  12 x  3x
f ( x)  x
3
2
A product has a profit function of
P( x)  .01x  60 x  500
2
for the production and sale of x
units. Is the profit increasing or
decreasing when 100 units have
been sold?
Since C(x) is the cost for producing x
units, the average cost for producing
x units is C(x) divided by x.
C ( x)
C ( x) 
x
The marginal average cost would be
found by taking the derivative.
Suppose a product has a cost
function given by
C ( x)  500  54 x  .03x ,0  x  1000
2
Find the average cost function.
Over what interval is the average
cost decreasing?
Assuming the graph is continuous (no
break) at the point where the function
changes from increasing to decreasing,
that point is called a relative maximum
point.
In the same manner, a relative
minimum point occurs when the
graph changes from decreasing to
increasing.
Determine the critical numbers for each
function and give the intervals where the
function is increasing or decreasing.
f ( x)  ( x  3)
2/3
f ( x)  x  7 x  3
2
1
f ( x)  1/ 4
x
x2
f ( x)  2
x 5
1 2
f ( x)  x  x  x  19
2
3
Page 315
problems 46, 47, & 48