Download Integrative Studies 410 Our Place in the Universe

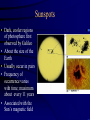
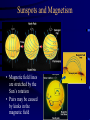
The Sun – A typical Star
• The only star in the solar
system
• Diameter: 100  that of Earth
• Mass: 300,000  that of Earth
• Density: 0.3  that of Earth
(comparable to the Jovians)
• Rotation period = 24.9 days
(equator), 29.8 days (poles)
• Temperature of visible surface
= 5800 K (about 10,000º F)
• Composition: Mostly hydrogen,
9% helium, traces of other
Solar Dynamics Observatory Video
elements
How do we know the Sun’s Diameter?
• Trickier than you might think
• We know only how big it appears
– It appears as big as the Moon
• Need to measure how far it is away
– Kepler’s laws don’t help (only relative
distances)
• Use two observations of Venus transit in
front of Sun
– Modern way: bounce radio signal off of Venus
How do we know the Sun’s Mass?
• Fairly easy calculation using Newton law of
universal gravity
• Again: need to know distance Earth-Sun
• General idea: the faster the Earth goes around
the Sun, the more gravitational pull  the
more massive the Sun
• Earth takes 1 year to travel 2π (93 million
miles)  Sun’s Mass = 300,000  that of
Earth
How do we know the Sun’s Density?
• Divide the Sun’s mass by its Volume
• Volume = 4π × (radius)3
• Conclusion: Since the Sun’s density is so low,
it must consist of very light materials
How do we know the Sun’s Temperature?
• Use the fact that the Sun is a “blackbody”
radiator
• It puts out its peak energy in visible light,
hence it must be about 6000 K at its surface
Black Body Spectrum
• Objects emit radiation of all frequencies,
but with different intensities
Ipeak
Higher Temp.
Ipeak
Ipeak
Lower Temp.
fpeak<fpeak <fpeak
How do we know the Sun’s rotation
period?
• Crude method: observe sunspots as they
travel around the Sun’s globe
• More accurate: measure Doppler shift of
spectral lines (blueshifted when coming
towards us, redshifted when receding).
– THE BIGGER THE SHIFT, THE HIGHER
THE VELOCITY
How do we know the Sun’s
composition?
• Take a spectrum of the Sun, i.e. let sunlight
fall unto a prism
• Map out the dark (Fraunhofer) lines in the
spectrum
• Compare with known lines (“fingerprints”)
of the chemical elements
• The more pronounced the lines, the more
abundant the element
Spectral Lines – Fingerprints of the Elements
• Can use spectra
to identify
elements on
distant objects!
• Different
elements yield
different
emission spectra
• The energy of the electron depends on orbit
• When an electron jumps from one orbital to another, it
emits (emission line) or absorbs (absorption line) a
photon of a certain energy
• The frequency of emitted or absorbed photon is related
to its energy
E=hf
(h is called Planck’s constant, f is frequency, another word for
color )
Sun 
Compare Sun’s
spectrum (above)
to the fingerprints
of the “usual
suspects” (right)
Hydrogen: B,F
Helium: C
Sodium: D
“Sun spectrum” is the sum of many
elements – some Earth-based!
The Sun’s spectrum in some detail
The Sun’s Spectrum
• The Balmer
line is very
thick  lots
of Hydrogen
on the Sun
• How did
Helium get its
name?
How do we know how much energy
the Sun produces each second?
• The Sun’s energy spreads out in
all directions
• We can measure how much
energy we receive on Earth
• At a distance of 1 A.U., each
square meter receives 1400 Watts
of power (the solar constant)
• Multiply by surface of sphere of
radius 149.6 bill. meter (=1 A.U.)
to obtain total power output of the
Sun
Energy Output of the Sun
• Total power output: 4  1026 Watts
• The same as
– 100 billion 1 megaton nuclear bombs per
second
– 4 trillion trillion 100 W light bulbs
– $10 quintillion (10 billion billion) worth of
energy per second @ 9¢/kWh
• The source of virtually all our energy
(fossil fuels, wind, waterfalls, …)
– Exceptions: nuclear power, geothermal
Where does the Energy come from?
• Anaxagoras (500-428 BC): Sun a large hot
rock – No, it would cool down too fast
• Combustion?
– No, it could last a few thousand years
• 19th Century – gravitational contraction?
– No! Even though the lifetime of sun would be
about 100 million years, geological evidence
showed that Earth was much older than this
What process can produce so much
power?
• For the longest time we did not know
• Only in the 1930’s had science advanced to
the point where we could answer this question
• Needed to develop very advanced physics:
quantum mechanics and nuclear physics
• Virtually the only process that can do it is
nuclear fusion
Nuclear
Fusion
• Atoms: electrons orbiting nuclei
• Chemistry deals only with
electron orbits (electron exchange
glues atoms together to from
molecules)
• Nuclear power comes from the
nucleus
• Nuclei are very small
– If electrons would orbit the
statehouse on I-270, the nucleus
would be a soccer ball in Gov.
Strickland’s office
– Nuclei: made out of protons (el.
positive) and neutrons (neutral)
Atom: Nucleus and
Electrons
The Structure of Matter
Nucleus: Protons and
Neutrons (Nucleons)
Nucleon: 3 Quarks
| 10-10m |
| 10-14m |
|10-15m|
Nuclear fusion reaction
–
–
–
In essence, 4 hydrogen nuclei combine (fuse) to
form a helium nucleus, plus some byproducts
(actually, a total of 6 nuclei are involved)
Mass of products is less than the original mass
The missing mass is emitted in the form of energy,
according to Einstein’s famous formulas:
E=
2
mc
(the speed of light is very large, so there is a
lot of energy in even a tiny mass)
Hydrogen fuses to Helium
Start: 4 + 2 protons  End: Helium nucleus + neutrinos
Hydrogen
fuses to
Helium
Could We Use This on Earth?
• Requirements:
– High temperature
– High density
– Very difficult to achieve on Earth!
Fusion is NOT fission!
• In nuclear fission one splits a large nucleus
into pieces to gain energy
• Build up larger nuclei Fusion
• Decompose into smaller nuclei Fission
Harvesting Binding Energy
Small harvest by decay
Big harvest by fusion
Most stable element in the universe
The Standard Solar Model (SSM)
• Sun is a gas ball of hydrogen & helium
• Density and temperature increase towards
center
• Very hot & dense core produces all the
energy by hydrogen nuclear fusion
• Energy is released in the form of EM
radiation and particles (neutrinos)
• Energy transport well understood in physics
Standard Solar Model
How much energy does the Sun
produce in theory?
• Short answer: As much as it has to …
• Longer answer: … to maintain hydrostatic
equilibrium
Hydrostatic Equilibrium
• Two forces compete: gravity (inward) and energy
pressure due to heat generated (outward)
• Stars neither shrink nor expand, they are in
hydrostatic equilibrium, i.e. the forces are equally
strong
Gravity
Heat
Gravity
More Mass means more Energy
• More mass means more gravitational
pressure
• More pressure means higher density,
temperature
• Higher density, temp. means faster reactions
& more reactions per time
• This means more energy is produced
Does too much Energy lead to
Explosion?
• No, there is regulative feedback:
– More energy produced means more radiative
pressure
– This means the stars gets bigger
– This means density, temperature falls off
– This means less reactions per time
– This means less energy produced
How do we know what happens in
the Sun?
• We can’t “look” into the Sun
• But: come up with theory that explains all the
features of the Sun and predicts new things
• Do more experiments to test predictions
• This lends plausibility to theory
Details
•
•
•
•
•
•
•
Radiation Zone and Convection Zone
Chromosphere
Photosphere
Corona
Sunspots
Solar Cycle
Flares & Prominences
Sunspots
• Dark, cooler regions
of photosphere first
observed by Galileo
• About the size of the
Earth
• Usually occur in pairs
• Frequency of
occurrence varies
with time; maximum
about every 11 years
• Associated with the
Sun’s magnetic field
Sunspots and Magnetism
• Magnetic field lines
are stretched by the
Sun’s rotation
• Pairs may be caused
by kinks in the
magnetic field
The Solar Cycle
Understanding Stars
• “Understanding” in the scientific sense
means coming up with a model that
describes how they “work”:
– Collecting data (Identify the stars)
– Analyzing data (Classify the stars)
– Building a theory (Explain the classes and their
differences)
– Making predictions
– Testing predictions by more observations
Identifying Stars - Star Names
• Some have names that go back to ancient times
(e.g. Castor and Pollux, Greek mythology)
• Some were named by Arab astronomers (e.g.
Aldebaran, Algol, etc.)
• Since the 17th century we use a scheme that lists
stars by constellation
– in order of their apparent brightness
– labeled alphabetically in Greek alphabet
– Alpha Centauri is the brightest star in constellation
Centaurus
• Some dim stars have names according to their
place in a catalogue (e.g. Ross 154)
Classification by Star Properties
• What properties can we measure?
–
–
–
–
–
–
–
distance
velocity
temperature
size
luminosity
chemical composition
mass
Distances to the Stars
• Parallax can be used out to about
100 light years
• The parsec:
– Distance in parsecs = 1/parallax (in
arc seconds)
– Thus a star with a measured
parallax of 1” is 1 parsec away
– 1 pc is about 3.3 light years
• The nearest star (Proxima
Centauri) is about 1.3 pc or 4.3
lyr away
– Solar system is less than 1/1000 lyr
Homework: Parallax
• Given p in arcseconds (”), use
d=1/p to calculate the distance
which will be in units “parsecs”
• By definition, d=1pc if p=1”, so
convert d to A.U. by using
trigonometry
• To calculate p for star with d given
in lightyears, use d=1/p but
convert ly to pc.
• Remember: 1 degree = 3600”
• Note: p is half the angle the star
moves in half a year