Download Graphing Linear Equations

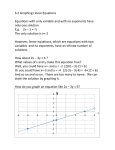
Graphing Linear Equations
Question 1: What is a rectangular coordinate system?
Answer 1:
The rectangular coordinate system is used to graph points and equations. To create the
rectangular coordinate system, use the following steps:
1. Draw a horizontal line.
2. Choose a point on the line. This point is called the origin and is assigned a value of 0.
3. Choose a length, called the scale, and mark it to the right of the origin. Continue
writing the measurements to create the positive integers.
4. Complete the same process on the left side of the origin as a reflection of the right
side, except these are all negative real numbers.
5. Draw a vertical line passing through the origin.
6. Label the real numbers the same as on the horizontal line, with the numbers above the
horizontal line as positive and the ones below the horizontal line as negative.
The horizontal line is usually called the x-axis, and the vertical line is the y-axis. These are
arbitrary names, and either axis can be called by any name the application may receive, such as
hours, miles, or area. The scaling also can be changed according to the need.
Points can be plotted on the coordinate system by using ordered pairs known as coordinates.
These points are denoted by using parentheses. For example, in the point (2, 3), 2 represents the
x-value, and 3 represents the y-value. To plot the points, you locate 2 on the x-axis, and then go
up vertically 3 units.
Question 2: How do you graph a linear equation?
Answer 2:
There are two ways you have learned to graph a linear equation:
Plotting Points
If given a set of points that represent a linear equation, plot each point on the rectangular
coordinate system, and connect the points to create the line. If an equation is given but no points
are given, find a set of points by choosing a value for x or y and solving for the other variable. It
is typically a good idea to choose three to five points. Once the points have been found, plot
them and connect them to create the line.
Slope and Y-Intercept
If given a linear equation, you can solve for y by isolating it on one side of the equation. Once y
is by itself, you then can find the y-intercept and slope of the graph. The slope is the term
multiplied by x, and the y-intercept is your constant. The slope-intercept form is generally given
as y = mx + b, where m is the slope and b is the y-intercept. Remember to plot the y-intercept
first, and then plot the next point by using the slope. The numerator of the slope represents the
change in y, and the denominator represents the change in x. Once you have plotted both points,
draw a line between the two points, and graph the equation of the line.
Question 3: Which of the following points (4, 5), (-6, 0), (3, -2), (-2, 2) are solutions to the
equation 2y = 6 + x?
Answer 3:
One way to answer this question is to plug each coordinate pair into the equation and determine
if the two sides are equivalent. If so, the pair is a solution to the equation. If the sides are not
equal, then the point is not a solution to the equation. For instance, refer to the following:
Note the coordinate pair (3, -2) does not satisfy the equation; however, the points (4, 5), (-6, 0),
and (-2, 2) are the solutions to the equation.
Another way to solve this problem is by graphing the equation of the line. If one of the points
falls on the line, then it is a solution to the equation. If the point does not fall on the line, it is not
a solution.
Question 4: Given the equation 2x + 3y = 12, how do you find the intercepts of the line?
Answer 4:
The x-intercept is the point on the linear graph where the graph intersects the x-axis. At this
point, the y value will always be 0. The y-intercept is the point on the linear graph where the
graph intersects the y-axis. At this point, the x value will always be 0.
To find the x-intercept, plug in the value of 0 for y and solve for x.
2x + 3y = 12
2x + 3(0) = 12
2x = 12
x=6
The x-intercept would be (6, 0).
To find the y-intercept, plug in the value of 0 for x, and solve for y.
2x + 3y = 12
2(0) + 3y = 12
3y = 12
y=4
The y-intercept would be (0, 4).
If you know the x- and y-intercepts of a linear equation, you can easily graph the line by plotting
each intercept and drawing the line through the points.
Question 5: What are the various forms of the equation of a line?
Answer 5:
The standard form of an equation of a line is ax + by + c = 0. This form shows that the function
is a line but does not give other information about the line. The standard form can be converted
to the slope-intercept form.
Every nonvertical line can be written in the slope-intercept form, which is y = mx + b, where m is
the slope of the line and b is the y-intercept. The y-intercept is the point where the line crosses
the y-axis. The slope is the steepness of the line and is calculated by the change in y divided by
the change in x for any two points on the line.
Question 6: Given the slope and y-intercept, how do you write an equation for a line?
Answer 6:
Given the slope of a line and the y-intercept, the equation of the line can be directly written in the
form y = mx + b, where m is the slope and b is the y-intercept. For example, if the slope is m = 2
and the y-intercept is 3, then the equation of the line is y = 2x + 3.
Question 7: When given two points, how do you find the slope, the y-intercept, and the equation
of the line?
Answer 7:
When given two points, the first step is to find the slope. To calculate the slope, divide the
difference in y values by the difference in x values. For example, if the line passes through the
two points (1, 1) and (3, 5), then the slope is (5 − 1) / (3 − 1) = 4 / 2 = 2.
To find b, use the calculated slope and either point to substitute in the slope-intercept form. The
slope-intercept form would be y = 2x + b; using (1, 1), substitute into the equation. This gives 1 =
2(1) + b, or b = -1. Input the information into slope-intercept form, where m = 2 and b = -1, and
the equation of the line is y = 2x − 1.
Question 8: What is the slope, the y-intercept, and the equation of the line that passes through
the points (-3, 5) and (3, -8)?
Answer 8:
Question 9: Given the equation, C = 650m + 400, what does each component represent?
Answer 9:
In the equation C = 650m + 400, m represents the number of months an apartment has been
rented, and C represents the rental cost by the end of mth month.
Slope
The value of the slope in this equation is 650, or 650/1. This value represents the change in y
(rental cost C) over the change in x (number of months m). Remember, the value in the
numerator represents y, and the value in the denominator represents x. Therefore, this value of
650 can be interpreted such that each month’s rent will cost $650.
Y-Intercept
The y-intercept in this equation is 400. The y-intercept of a graph occurs when the x value is 0. If
the x value (number of months m) is zero, then the y-value (rental cost C) is 400. What does that
mean? Before one starts to pay the monthly rent (i.e., the zero month), one must pay a certain
amount of money down, typically called the security deposit. Thus, this apartment will cost $650
a month plus a $400 security deposit.
Increasing or Decreasing
The graph of the line should be increasing because it contains a positive slope of $650.
Question 10: Given a graph, what is the rate of change and the representative linear equation?
Answer 10:
The following graph shows the increase of gas prices in the last 6 months.
Rate of Change
The rate of change is another term for the slope of the line. The slope is defined as the change in
y over the change in x. In this real-world problem, the y-values are represented by the price of the
gas, and the x-values are represented by time in months. The goal is to try to find the rate of
change of the gas prices compared between the months. Choosing two points on the line and
finding the slope can do this.
The rate of change is 0.25, meaning that each month, the gas price rises 25¢.
Linear Equation
Because the rate of change or the slope is known, use the formula to find the equation of the line.
Plug in the slope, choose a point from the graph to plug in for x and y, and then simplify to find
b. Once b is found, plug that value back into the equation to find the equation of the line.