* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download linear function
Functional decomposition wikipedia , lookup
Big O notation wikipedia , lookup
Principia Mathematica wikipedia , lookup
Bra–ket notation wikipedia , lookup
Dirac delta function wikipedia , lookup
Function (mathematics) wikipedia , lookup
History of the function concept wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
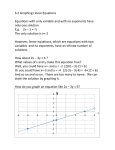
8-4 Linear Functions Warm Up Problem of the Day Lesson Presentation Lesson Quizzes 8-4 Linear Functions Warm Up Determine if each relationship represents a function. 1. yes 2. y = 3x2 – 1 yes 3. For the function y = x2 + 2, find when x = 0, x = 3, and x = –2. 2, 11, 6 8-4 Linear Functions Problem of the Day Take the first 20 terms of the geometric sequence 1, 2, 4, 8, 16, 32, . . . .Why can’t you put those 20 numbers into two groups such that each group has the same sum? All the numbers except 1 are even, so the sum of the 20 numbers is odd and cannot be divided into two equal integer sums. 8-4 Linear Functions Sunshine State Standards MA.8.A.1.2 Interpret the slope and the xand y-intercepts when graphing a linear equation for a real-world problem. Also MA.8.A.1.1 8-4 Linear Functions Vocabulary linear function function notation 8-4 Linear Functions A linear function is a function that can be described by a linear equation. One way to write a linear function is by using function notation. If x represents the input value, then the and y represents the output value, the function notation for y is f(x), where f names the function. Any linear function can be written in slopeintercept form f(x) = mx +b where m is the slope of the function’s graph and b is the y-intercept. 8-4 Linear Functions Additional Example 1A: Identifying Linear Functions Determine whether the function f(x) = 2x3 is linear. If so, give the slope and y-intercept of the function’s graph. The function is not linear because x has an exponent other than 1. The function cannot be written in the form f(x) = mx + b. 8-4 Linear Functions Additional Example 1B: Identifying Linear Functions Determine whether the function f(x) = 3x + 3x + 3 is linear. If so, give the slope and yintercept of the function’s graph. f(x) = 3x +3x + 3 Write the equation in slopeintercept form. f(x) = 6x + 3 Combine like terms. The function is linear because it can be written in the form f(x) = mx + b. The slope m is 6, and the y-intercept b is 3. 8-4 Linear Functions Check It Out: Example 1A Determine whether each function is linear. If so, give the slope and y-intercept of the function’s graph. f(x) = –2x + 4 m = –2; b = 4; f(x) = –2x + 4 is a linear function because it can be written in the form f(x) = mx + b. 8-4 Linear Functions Check It Out: Example 1B Determine whether each function is linear. If so, give the slope and y-intercept of the function’s graph. f(x) =– 1 + 4 x f(x) =– 1 + 4 is not a linear function because x x appears in a denominator. 8-4 Linear Functions Additional Example 2A: Writing the Equation for a Linear Function Write a rule for the linear function. Step 1: Identify the y-intercept b from the graph. b=2 Step 2: Locate another point on the graph, such as (1, 4). Step 3: Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for m. 8-4 Linear Functions Additional Example 2A Continued f(x) = 4= 4= –2 2= mx + b m(1) + 2 m+2 –2 m The rule is f(x) = 2x + 2. (x, y) = (1, 4) 8-4 Linear Functions Additional Example 2B: Writing the Equation for a Linear Function Write a rule for the linear function. x y Step 1: Locate two points. –3 –8 (1, 4) and (3, 10) –1 –2 Step 2: Find the slope m. 1 4 3 10 y2 – y1 10 – 4 6 m = x2 – x1 = = =3 3–1 2 Step 3: Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for b. 8-4 Linear Functions Additional Example 2B Continued f(x) = mx + b 4 = 3(1) + b 4= 3+b –3 –3 1= b The rule is f(x) = 3x + 1. (x, y) = (1, 4) 8-4 Linear Functions Check It Out: Example 2A Write a rule for each linear function. 8-4 Linear Functions Check It Out: Example 2A Continued b = 1; (5, 2): 2 = m(5) + 1 1 = m; f(x) = 1 x + 1 5 5 8-4 Linear Functions Check It Out: Example 2B Write a rule for the linear function. x y –2 –1 0 –5 –3 –1 1 1 2 3 (0, –1) and (1, 1); m = 1 –(–1) = 2 1–0 b = –1; f(x) = 2x – 1 8-4 Linear Functions Example 3: Money Application A video game club cost $15 to join. Each game that is rented costs $1.50. Find a rule for the linear function that describes the total cost of renting videos as a member of the club, and find the total cost of renting 12 videos. To write the rule, determine the slope and y-intercept. m = 1.5 b = 15 The rate of change is $1.50 per game. The cost to join is $15. f(x) = 1.5x + 15 f(x) is the cost of renting games, and x is the number of games rented. f(x) = 1.5(12) + 15 f(x) = 18 + 15 To rent 12 games as a member will = 33 cost $33. 8-4 Linear Functions Check It Out: Example 3 A book club has a membership fee of $20. Each book purchased costs $2. Find a rule for the linear function that describes the total cost of buying books as a member of the club, and find the total cost of buying 10 books. rate of change = $2 per book; y-intercept is $20 membership fee; f(x) = 2x + 20 f(10) = 2(10) + 20 = 20 + 20 = 40 The total cost of buying 10 books is $40. 8-4 Linear Functions Lesson Quizzes Standard Lesson Quiz Lesson Quiz for Student Response Systems 8-4 Linear Functions Lesson Quiz: Part I Determine whether each function is linear. If so, give the slope and y-intercept of the function’s graph. 1. f(x) = 4x2 not linear 2. f(x) = 3(x + 4) linear; m = 3; b = 12 Write the rule for the linear function. 3. f(x) = 1 x - 1 2 8-4 Linear Functions Lesson Quiz: Part II Write the rule for each linear function. 2. x y –3 0 3 –10 –1 8 5 7 14 20 f(x) = 3x – 1 3. Andre sells toys at the craft fair. He pays $60 to rent the booth. Materials for his toys are $4.50 per toy. Find a rule for the linear function that describes Andre's expenses for the day. Determine his expenses if he made 25 toys. f(x) = 4.50x + 60; $172.50 8-4 Linear Functions Lesson Quiz for Student Response Systems 1. Identify a function that is linear. A. f(x) = 4x2 B. f(x) = 2(x2 + 1) C. f(x) = 2(x + x) D. f(x) = x2 8-4 Linear Functions Lesson Quiz for Student Response Systems 2. Identify a function that is not linear. A. f(x) = x B. f(x) = 0.5x C. f(x) = 3(x + x) + 2 D. f(x) = 5x2 8-4 Linear Functions Lesson Quiz for Student Response Systems 3. Write the rule for the linear function. A. f(x) = x+3 B. f(x) = –x + 3 C. f(x) = x+3 D. f(x) = 3x + 3