Download continuous - UMass Math

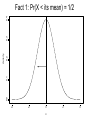
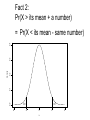
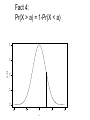
More Examples:
• There are 4 security checkpoints. The probability of being searched
at any one is 0.2. You may be searched more than once in total and
all searches are independent. What’s the probability of being
searched at least one time?
• 50 geese in a flock of 200 are tagged by a wildlife biologist. The next
year, 10 geese from the flock are captured. Assume the flock still
has (the same) 200 geese and no tags are lost. What’s the
probability that at least 5 of the recaptured geese have tags?
• Suppose a written test has 5 True/False questions. Passing = at
least 3 correct answers and the test can be taken at most 3 times.
(Assume no learning occurs between tests if one fails!)
– If one randomly guesses what’s the probability of passing?
– What’s the probability that someone who randomly guesses will
eventually pass?
• An overloaded server receives an average of 25 emails per second
at 12:00PM. If it receives more than 30 emails in a second, it will
crash. What’s the probability of a crash at 12:00PM on a given day
(based on the traffic in the previous 1 second)?
Answers to Examples
1. X = number of times searched. X has a binomial
distribution with n=4 and p=0.2. We want Pr(X>0) = 1Pr(X=0)
2. X = number of recaptured geese w/ tags. X has a
hypergeometric distribution with N = 200, M = 50, n=10.
We want Pr(X>=5) =
Pr(X=5)+Pr(X=6)+Pr(X=7)+Pr(X=8)+Pr(X=9)+Pr(X=10)
3. X = number of questions right. X has a binomial
distribution with n = 5 and p=0.5. Want Pr(X>=3) =
Pr(X=3)+Pr(X=4)+Pr(X=5)
4. Pr eventually pass = Pr(Pass on first try or fail first and
then pass or fail twice and then pass) = Pr(X>=3) +
Pr(X<3)*Pr(X>=3) + Pr(X<3)*Pr(X<3)*Pr(X>=3)
5. X = number of emails in a second. X has a Poisson
distribution with rate = 25 per second. Want Pr(X>30) =
1-Pr(X<=30) = Pr(X=0)+…+Pr(X=30)
(in each case, once you know the distribution and the
parameters, the Pr(X=k) can be calculated with the pdf.)
• If you’re interested in polls, an
interesting “statistics related”
website is: www.gallup.com
• Polls that ask questions w/ 2
answers are related to the
binomial distribution:
From gallup.com (Feb 19, 2003)
n = 483
– n = number of people asked
– p = probability of one of the
answers
– Note that a poll uses data to
estimate p
(i.e. estimate of p = number of
yeses / n)
Example: X = number of people
who think “unfinished business
is the reason.
X has a Bin(483,0.31) distribution
(assume 0.31 is the true p).
Example:
• Suppose 10 people are polled:
– Is a terrorist attack at least somewhat likely at the
Olympics?
• Suppose p=0.31
• Q: What’s the probability that fewer than 9
people say yes?
• A: Let X ~ Bin(10,0.31)
Want Pr(X<9) = 1-Pr(X=9)-Pr(X=10)
=1-(10 choose 9)(0.319)(0.691)
-(10 choose 10)(0.3110)(0.690)
=1-0.0000-0.0002 = 0.9998
Example: Dietary Data
Percent
• As part of an
epidemiological study,
physicians measured
the amount of folate
in the diets of 545
people.
• What’s the probability
that a new person’s
folate consumption
equals exactly 5.5?
Histogram from observed sample
20
10
0
3.5
4.5
5.5
6.5
7.5
Folate (Calorie Adjusted mg)
Question about the random variable
describing dietary folate of a new
person.
• In the folate example, if folate were
measured accurately enough, the
probability of seeing any exact value on a
new person is zero.
• Note that this is different from random
variables like “the number of questions
right on a test, etc”.
– The folate example gives an example of
continuous data.
– Probability can be applied to the probability
that a continuous random variable is in an
interval, but any particular value has zero
probablity.
Chapter 6:
Continuous Distributions & Normality
• Up to this point, all random variables have
been discrete:
– Possible values are integers (any integer or a
subset):
• Binomial(n,p) random variables can be 0 or 1 or …or n.
• Poisson(rate) random variables can be 0 or 1 or …
• Hypergeometric(N,M,n) random variables can be 0 or 1
or …or n.
• PDFs give probabilities that the random variables take
on any of these values
• CDFs give probabilities that the random variables are
less than or equal to a certain value
• Random variables that can take on any
real number are continuous.
• Continuous random variables have
probability density functions (pdfs) too.
• Again, they are models for how the
random variables behave.
• The probability that a continuous random
variable is in an interval is the area under
the pdf in that interval.
PDF for the Folate Data (assume we know this function):
Pr(5 < random person’s folate intake < 6) = 0.54
6
= shaded area (i.e.
Pr(5  folate  6)   folate' s pdf ( x)dx
0.4
0.2
0.0
Density
0.6
0.8
5
4
5
6
Folate
7
8
)
• Continuous PDFs :
– notation: f(x)
– f(x) is greater than or equal to zero.
– All the area under f(x) is 1.
– i.e.

Pr(   X  ) 
 f ( x)dx  1

y
– CDF: Pr( X  y )   f ( x)dx

Let a be a number.
For a continuous random variable X:
Pr( X  a)  Pr( X  a)
Continuous pdfs will be known
functions
• Most commonly used:
0.2
0.0
0.1
density
0.3
0.4
– Normal or Gaussian distribution (“bell curve”)
– We’ll see why this is so common in a few weeks.
-4
-2
0
x
2
– 2 parameters: mean m and std dev s
4
2 normal distibutions:
Both have the same mean (0).
Narrower one has a std
dev of 2.
Fatter one has std dev
of 1.
0.2
0.4
Smaller standard deviation
means that the model says
the data are more likely to
be concentrated around
the mean.
0.0
density
0.6
0.8
Mean = center of normal distribution
-4
-2
0
x
2
4
The normal pdf is this functinon:
[1/(ssqrt(2p))]e[-0.5((x-m)/s)2]
Determining normal probabilities:
• Suppose X has a normal distribution with mean
5 and std dev 2.
• Notation X~N(5,4)
[notation uses N(mean,variance)]
• What’s the probability that X is less than 7?
• It turns out that no one can “solve” the integral
that defines this probability.
• As a result, we need to use tables, computers,
or calculators to compute normal probabilities.
0.20
0.15
0.10
0.05
0.0
density
Pr(X<7) = area under
curve to left of x=7
0
5
x
7
10
0.2
0.1
0.0
density
0.3
0.4
Fact 1: Pr(X < its mean) = 1/2
-4
-2
0
x
2
4
Fact 2:
Pr(X > its mean + a number)
0.2
0.1
0.0
density
0.3
0.4
= Pr(X < its mean - same number)
-4
-2
0
x
2
4
0.4
Fact 3:
Assume a > b.
Pr(b< X < a) = Pr(X<a)-Pr(X<b)
0.2
0.1
0.0
density
0.3
Area under curve
Between a and b
Is area under curve
To the left of a minus
The area under the
curve to the left of
b.
-4
-2
b
0
x
a
2
4
0.2
0.1
0.0
density
0.3
0.4
Fact 4:
Pr(X > a) = 1-Pr(X < a)
-4
-2
0
x
2
4
0.2
0.1
0.0
density
0.3
0.4
Fact 5: Tables inside the cover of
your book are given in terms of
Pr(0<Z<a) (where a>0 and Z~N(0,1))
(Tables with P(Z<a) are in Appendix 1)
-4
-2
0
x
a
2
4
Table in book: (inside cover)
Z
.00 .01 .02 .03 .04…
0.0 .0000 .0040 .0120 .0160 .0199
0.1 .0398 .0438 .0478 .0517 .0557
0.2 .0793 .0832 .0871 .0910 .0948
Hundredths
Ones
and
.
place
tenths places
.
Pr(0 < Z < 0.13) = 0.0517
.
This is the upper
left hand corner
of the table.
Using Tables: 4 Easy Steps
Want Pr(X<7)
1. Draw picture (next page) (allows use of common sense)
2. Translate X to a normal random variable with mean 0 and
std dev 1 (called “Z”, a standard normal r.v.)
–
Do this by “centering and scaling”:
•
Rule: If X~N(5,4) then (X-5)/2 ~N(0,1)
3. Manipulate to get in terms of Pr(Z<a) form
–
So, Pr(X<7)
= Pr( (X-5)/2 < (7-5)/2)
= Pr( Z < 1) where Z~N(0,1)
4. Look up in table: Pr(X<7)
= Pr(Z<1)
= 0.8413
0.20
0.15
0.10
0.05
0.0
density
Pr(X<7) = area under
curve to left of x=7
0
5
x
7
10
• What’s Pr(X < 4)?
• Draw (on next page)
• Center and scale:
– Pr(X<4)
• Look up
= Pr( (X-5)/2 < (4-5)/2 )
= Pr( Z < -1/2 )
= 0.3085
0.20
0.15
0.10
0.05
0.0
density
Pr(X<4) = area under
curve to left of x=4
0
5
x
7
10