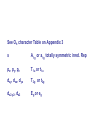* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Crystal-Field Theory Ligand-Field or Molecular Orbital Theory
Survey
Document related concepts
Transcript
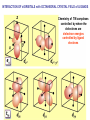
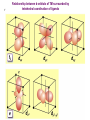
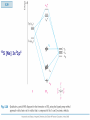
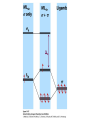
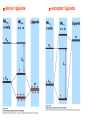
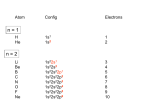
How can we explain bonding between metals and ligands? Crystal-Field Theory Ligand-Field or Molecular Orbital Theory October 4, 2010 The Periodic Table Electronic structure of transition metals Filled ns, np shells; chemistry defined by unoccupied nd-orbitals Number of d-electrons = Z – nearest noble gas e’s – charge e.g.: Fe(II) = 26 – 18 – 2 =6 Fe(III) = 26 – 18 – 3 = 5 d2z2-y2-x2 Valence Bond (VB) Theory developed by Pauling in the 1930s - used in VSEPR Useful in d-complexes sp3d, sp3d2, sp2d useful in CN = 5 (sp, tbp), 6 (octahedral), and 4 (square plana Not much used for d- coplexes today, but some of the terminology is essential Note limitations: M needs 3dx2-y2, 3dz2, 4s, 4px, 4py, 4pz to be unoccupied applying VB: 3d 4s 4p Cr+3 d2sp3 [Cr(NH3)6]+3 OK for all d3 Fe3+ d5 LS: ↑↓ ↑↓ ↑ 3d ↑↓ ↑↓ ↑↓ ↑↓ ↑↓ ↑↓ OK d2sp3 Now consider Fe 3+ d5 HS octahedral: d2sp3 ↑ ↑ ↑ ↑ ↑ ↑↓ ↑↓ ↑↓ ↑↓ ↑↓ ↑↓ sp3d2, but 4d? d8 octahedral case 3d 4s 4p 4d Ni+2 high spin sp3d2 again 4d [Ni(NH3)6]+2 [Ni(L)4]2+ Tetrahedral case: 4L e- pair goes to sp3, OK, paramagnetic Square planar case: dsp2 ↑↓ ↑↓ ↑↓ ↑↓ 3d(z2, xy, xz, yz) ↑↓ ↑↓ ↑↓ ↑↓ (dx2-y2)sp2 V B VB can rationalize geometry and magnetic properties on a simple level cannot say anything about electronic spectra (color) and why some ligands lead to HS and some to LS complexes why LS d6 complexes are kinetically inert etc.. Need better theory! Crystal-Field Theory (gross over-simplification) d2z2-y2-x2 INTERACTION OF d-ORBITALS with OCTAHEDRAL CRYSTAL FIELD of LIGANDS Chemistry of TM complexes controlled by where the d-electrons are d-electron energies controlled by ligand electrons charges charges 10Dq, a.k.a. ∆ Definition: energy splitting between the t2g and eg orbitals Measurement: eg hν ∆E = 10Dq t2g [Ti(III)(H2O)6]3+ d-electrons = 22 - 18 – 3 = 1 hν = 20,300 cm-1 = green light (complex = violet) = 58.04 kcal/mol (on the order of a bond) ∆oct = E= hν Ti3+ d1 l Spectrochemical series of ligands Spectrochemical series of metal ions Mn2+<Ni2+<Co2+<Fe2+<V2+<Fe3+,Co3+<Mn4+<Mo3+<Rh3+<Ru3+<Pd4+<Ir3+<Pt4+ Strong and weak field Factors affecting 10 Dq -Increased charge on metal: draws ligands in more closely; more effect on d-orbital splitting -Ligand type: spectrochemical series -So named because “strong field” ligands have higher energy d-d transitions (shorter wavelength UV/vis maxima) I- < Br- < S2- < Cl- < NO3- < OH- ~ RCOO- < H2O ~ RS- < NH3 ~ Im < 1,2-diaminoethane < bipy < CN-, CO d2 Case Electronic configuration is same for strong or weak field case d3 Case Electronic configuration is same for strong or weak field case d4 Weak Field – High Spin (HS) Case ∆o < Ep, pairing energy S=2 4 d Strong Field – Low Spin Case ∆o > Ep, pairing energy S=1 Electron pairing Ions with equal and greater than d4 electronic configuration in octahedral (Oh) coordination can have low and high spin forms depending on value of ∆o (10Dq) octahedral Fe3+ (d5) Low spin eg ∆o=10 Dq t2g P = spin pairing energy High spin eg ∆o =10 Dq t2g smaller than ∆o: S = ½ spin pairing energy larger than ∆o: S = 5/2 LS: ∆o > P HS: ∆o < P Unpaired (non-integer) spin: paramagnetic - detectable by magnetic measurement or sometimes by EPR Crystal-field Stabilization Energy (CFSE) CFSE = x(-4Dq) + y(+6Dq) or since ∆o = 10 Dq CFSE = x(-0.4∆o) + y(+0.6∆o) where x = number of electrons in t2g (lower levels) y = number of electrons in eg (upper levels) Crystal-Field Stabilization Energy, CFSE or Ligand-Field Stabilization Energy, LFSE d1 d2 = -0.8 ∆o Low Spin LFSE = -0.4∆o High Spin CFSE = x(-0.4 ∆o) + y(0.6 ∆o) d3 = -1.2 ∆o High Spin Low Spin d4 LFSE = -0.6 ∆o -1.6 ∆o + P d5 0 -2 ∆o + 2P Pairing Energy, P Two terms contribute to P: 1. loss of exchange energy p3 — — — or — — — E 2 E 1 > E2 E1 total exchange energy = Σ N ( N − 1) K 2 N = number of e- with parallel spin K = exchange energy (characteristic of atom or ion) e.g., ∆E = E2-E1 2. coulombic repulsion between paired e- Crystal-Field Stabilization Energy, CFSE or LFSE CFSE = x(-0.4∆o) + y(+0.6 ∆o) High Spin High Spin Low Spin d6 Low Spin d7 LFSE = -0.4 ∆o + P -2.4 ∆o + 2P d8 LFSE = d10 d9 -1.2 ∆o -0.8 ∆o -0.6 ∆o 0 Note: largest CFSE-LFSE for LS, d6 -1.8 ∆o + P r Relationship between d-orbitals of TM surrounded by tetrahedral coordination of ligands Octahedral vs Tetrahedral Splitting Pattern of d-Orbitals ∆tet = 4/9; ∆tet ≅ 1/2 ∆o tetrahedral octahedral ∆O > ∆T thus no strong field vs. weak field cases for tetrahedral complexes; note absence of subscript g in tetrahedral (t and e) Color of tetrahedral complexes different Octahedral HS tetrahedral S=½ 1 unpaired e- Co(II) d7 S = 3/2 3 unpaired e- Total spin quantum #: S ≡ Σ si N Σ = Summing over N electrons with si spin quantum # on each elelctron si = ±1/2 Jahn-Teller Effect: Cu2+ d9 J-T theorem: any nonlinear molecule in a degenerate electronic state will be unstable and will undergo a distortion to a system of lower symmetry and lower energy thereby removing the degeneracy J-T active ions: Strong JT: HS-d4, d9 [LS d7]– eg orbitals Weak JT: d1, d2, LS-d4, LS-d5, HS d7 – t2g J-T does not predict if distortion is: elongation along z (as shown) or elongation along x-y, lowering dx2-y2 Would you expect JT in Td d4 and d9? SQUARE PLANAR COMLEXES elongation of M-L along z second and third row d8 complexes are square planar. E.g., Pd (II), Pt(II), Rh(I), Ir(I) Square-planar Splitting Pattern of dOrbitals Ni2+, d8 [Ni(CN)4]-2 Square planar Ni2+ complex is diamagnetic S=0 Chapter 21 (20), self study on pg. 646 (564) d8 complexes:[NiCl4]2- paramagnetic, S=1; and Ni(CN)4]2- diamagnetic tetrahedral Squareplanar - --- -- -- Thermodynamic Aspects of LFSE Lattice Energies of MCl2 compounds M2+: Ca Sc Ti V Cr Mn Fe Co Same for MF2, MF3 and [MF6]3- complexes Ni Cu Zn Deviation from d0, d5 and d10 is due to thermochemical LFSE Agreement between e.g.: [Ni(H2O)6]2+, LFSE (thermochemical), 120 kJ/mol and LFSE (spectroscopic), 126 kJ/mol (1.2∆oct deter. From spectra of [Ni(H2O)6]2+, ∆oct 8500 cm-1) Must remember that LFSE is <10% of the total in reaction energies M2+ (aq) + H2O (l) → [M(H2O)6]2+ (aq) Ni2+ Octahedral vs Tetrahedral coordination Fig. 20.26 suggests that for d0, d5, and d10 there should be no preference for octahedral or tetrahedral coordination; there is a large preference for octahedral for d3 and HS d8 Case of spinels: MgAl2O6 mineral spinel; Mg2+ in Td while Al3+ in Oh site many analogous “normal” spinel compounds with A2+(M3+)2O6 -LFSE can favor the formation of so-called inverse spinels: e.g. normal: Fe(II)[(Cr(III)]2O4 LFSE [Cr(III) d3 1.2 ∆oct] > LFSE Fe(II) d6 (HS, -0.4 ∆oct) Fe3+(Fe2+, Fe3+)O4 LFSE = 0 for Fe3+ (d5), but Fe2+ (d6) provides -0.4∆oct What about Mn3O4, Co3O4 Review Chapter MO Theory: Chapter 2 Shriver and Atkins Molecular Orbital Theory of Octahedral Complexes-[ML6]n+ See Oh character Table on Appendix 3 s A1g or a1g totally symmetric irred. Rep px, py, pz T1u or t1u dxy, dxz, dyz T2g or t2g dx2-y2, dz2 Eg or eg X2+y2+z2 2z2-x2-y2, x2-y2 xy, xz, yz x, y, z, Molecular Orbital Theory – Octahedral complexes X2+y2+z2 2z2-x2-y2, x2-y2 xy, xz, yz x, y, z, 16S [Ne] 3s23p4 M – L σ - bonding in a [ML6]n+ complex M-L only σ bonding Bonding Model Example:[ Mo(CO)6] Mo: 5s1 4d5 – 6e6CO: 12 eTotal of 18 e- fill into MOs: [CoF6]3- High Spin (HS) a1g2, t1u6, eg4, t2g6 Low Spin (LS) Co3+ : d6 – 6e6F-: 6x2 - 12e- Total: 18 ea1g2, t1u6, eg4, t2g4 eg*2 so far not so different from CFT as far as t2g & eg orbital splitting, filling in [ML6]n+ Considering M-L π Bonding difference between CFT and LFT dπ-pπ dπ -dπ dπ-pπ* dπ-σ* Consider t2g set of ligand π-orbitals for Oh complex along x and z directions interacting with dxz M orbital z px and pz LGO π-interaction wirh dxz bonding and antibonding x Effect of π bonding with π-donating ligands: e.g., F-, Br-, Cl-, I- electrons from π-donor L fill t2g π orbitals electrons from M fill t2g* hence ∆O < no π-bonding M – L π-bonding with π*-accapter ligands e.g., R3N, CN-, CO M – L π-bonding with π*-acceptor ligands: e.g., R3N, CN-, CO d-block metal organometallic complexes and related complexes tend to obey the effective atomic number rule, or 18-electron rule 6 L provide 12 σ-bonding, a1g2, t1u6, eg4, e- from M fill t2g For π-acceptor ligands, d electrons from M occupy t2g since occupation of eg* is detrimental to M-L bond formation (∆O is large!), π-acceptor ligands are not favored for d7, d8, d9, d10 A low oxidation state organometallic complex contains π-acceptor Ls and the M center tends to acquire 18 e- in its valence shell (the 18-electron rule) and filling the valence orbitals: a1g2, t1u6, eg4, t2g6 LS π-donor ligands π-acceptor ligands Conclusions For complexes with σ-donor, π-donor and π-acceptor ligands: •∆o decreases with π-bonding donor ligands •Increased π donation stabilizes the t2g orbitals, and destabilizes t2g* , decreasing ∆o •π-acceptor ligands stabilize t2g level, and increase ∆o •∆o is relatively large for π-acceptor ligands, thus they tend to be low spin Observed spectrochemical series is explained: I-, Br-, π-donating ligands are weak field (small ∆o) CO, NO, CN- π-acceptor ligands, are strong field (large ∆o)