Download Series and Parallel Wiring

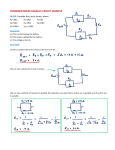
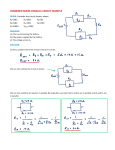
Series and Parallel Wiring
So far in dealing with electric circuits, we have only dealt
with one device in a circuit, such as a resistor or a light
bulb.
However, there are great many circuits that have more
than one component in them and use the same voltage
source.
There are two ways of wiring a circuit that exploits
different aspects of the voltage source. The first is series
wiring.
Series Wiring means that the devices are connected in
such a way that there is the same electric current going
through each device.
For example:
Resistors in Series
The drawing indicates that the voltage across resistor 1
is V1 and across 2 is V2 so that the total voltage is:
V = V 1 + V2
By applying the definition of resistance, we see that:
V = V1+V2 = IR1+IR2 = I (R1+R2) = IRs
Where Rs is called the equivalent resistance. Thus,
two resistors in series are equivalent to a single resistor
whose resistance is:
Rs = R1+R2
We can extend this to any number of resistors
connected in series:
Rs = R1+R2+R3+ …
Resistors in Series
The following example illustrates resistors in series:
The most memorable and most frustrating of any
series wiring is the old strands of Christmas lights:
If one bulb went out the whole strand did because the
current had no way of passing over the bad bulb. Parallel
wiring solved this problem.
Parallel Wiring
Parallel Wiring means that the devices are connected
in such a way that the same voltage is applied across each
device.
The following figure illustrates two resistors wired in
parallel:
Parallel wiring is seen in everyday in household
outlets. You can plug many devices into an outlet because
the same voltage will be applied to each device.
Resistors in Parallel
You can think of parallel wiring as water flowing
through a pipe once again. In the above circuit, each
resistor receives current from the battery as if the other
wasn’t there.
Therefore, R1 and R2 together draw more current from
the battery than either resistor alone.
Thus, according to Ohm’s law, a larger current arises
from a smaller resistance, so the total resistance is smaller
than either R1 or R2.
If two pipes are connected in parallel to a water pump
and are then replaced by a single pipe of the same cross
sectional area, the larger pipe will be able to push more
current through it than either one of the narrower pipes
before.
Resistors in Parallel
By connecting resistors in parallel, we reduce the
overall resistance. Going back to Ohm’s law:
I = I1+I2 = V/R1 + V/R2 = V (1/R1+R2) = V/Rs
Where once again, Rs is the equivalent resistance.
Thus, for two resistors wired in parallel the equivalent
resistance is given as:
1/Rs = 1/R1 + 1/R2
Furthermore, we can extend this to any number of
resistors wired in parallel:
1/Rs = 1/R1 + 1/R2 + 1/R3 + …
Because the new strands of Christmas lights are wired
in parallel and not series, if one burns out, the rest will
remain on.
Internal Resistance
Every electrical device, whether it is a battery,
lightbulb, electric speaker, etc… has in it a certain internal
resistance. We represent internal resistance as a small
resistor wired in series with the device. For example, as in
the case of the battery:
The wires and battery in a car have a certain internal
resistance. Also, when you are jumping a car, the jumper
cables have an internal resistance. Why then do we always
jump a car positive to positive and negative to negative?
Let’s calculate why. Assume the following:
What is current flowing through each?
Kirchhoff’s Rules
In an electric circuit that has many devices, it might
not be easy to separate the resistors in parallel or series.
Furthermore, you might have several batteries contained in
the circuit as well.
Kirchhoff was the first one to come up with 2 laws to
find the currents and resistances in an electric circuit. They
are called the loop rule and the junction rule.
The junction rule states that the total current directed
in a junction must equal the total current directed out of the
junction. For example:
The loop rule states that for a closed circuit loop, the
total of all the potential rises must equal all of the potential
drops. For example:
We can apply Kirchoff’s laws to any number of
situations involving resistors, batteries and capacitors. We
will try a few…
Measuring Current and Voltage
The devices that you used in the resistivity lab were
called an ammeter and a voltmeter. An ammeter will
measure the current going through the circuit and a
voltmeter will measure the voltage across a device. For
this reason, they have to be wired in the circuit differently.
Q. How do we wire an ammeter?
A. In series:
Q. How do we wire a voltmeter?
A. In parallel:
Capacitors in Parallel
In order to answer this question we have to remind
ourselves of how the capacitance is related to voltage.
Recall:
q = CV
In a parallel circuit, the charge is distributed between 2
capacitors from one battery. However the total charge must
be conserved so:
q = q1+q2= C1V+C2V = V(C1+C2) = VCp
Where now Cp is the equivalent capacitance of the
circuit. Thus, for capacitors wired in parallel,
Cp = C1+C2+C3+ …
Capacitors in Series
In a series circuit, all capacitors regardless of their
capacitances contain charge of the same magnitude. Thus,
the voltages across two capacitors must equal the total
voltage of the battery:
V = V1+V2 = q/C1+q/C2 = q(1/C1+1/C2) = q/Cp
Thus we can replace capacitors in a series by an
equivalent capacitance equal to:
1/Cp = 1/C1 + 1/C2 + 1/C3 + …
Furthermore, for any circuit, the loop laws of
Kirchhoff can be applied across a capacitor as well as a
resistor. However, it gets REALLY difficult because
capacitors have a very strange property.
Capacitors need to “charge up”. And they do so in an
exponential fashion.
RC Circuits
If a capacitor and a resistor are in a circuit together,
the way a capacitor charges depends on the resistance and
the capacitance of the devices:
A capacitor charges according to the following law:
q = qo (1-e-t/(RC))
The term RC in the exponent is called the time
constant of the circuit. It is measured in seconds and is a
measure of how difficult or how easy it is to charge up the
capacitor.
Likewise,
following law:
discharging
a
capacitor
q = qo e-t/(RC)
follows
the
The charging/discharging of a capacitor has many
applications. Heart pacemakers use them to control the
timing of voltage pulses delivered to a malfunctioning
heart.