Download Sections 5.2A (cont) and 5.2B: Uses of Right Triangles, and Trig on

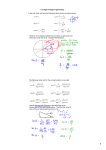
Sections 5.2A (cont) and 5.2B: Uses of Right Triangles, and Trig on the Unit Circle
Two Equations, Two Unknowns Revisited
This next kind of problem is fairly esoteric, but it shows off some good skills. You’ll get questions giving
you two equations sort of like
cos x + 2 sin x =
11
5
2 cos x + sin x =
10
5
and after that, you need to find trig functions like sec(x) or cot(x). There are two main ideas we’ll use here:
1. This is a two-unknown system “in disguise.” For instance, if we say C = cos x and S = sin x, we get
C + 2S = 11/5
2C + S = 10/5
which can be solved by the elimination method.
2. Once you know C and S (i.e. cos and sin), you can use them to get any other trig function.
Ex 1: Assume cos(x) + 3 sin(x) = 15/5 and 2 cos(x) + sin(x) = 10/5. Find sec(x) and tan(x).
SPECIAL ANGLES
There are a few acute angles whose trig values can be computed by hand, called the special angles. They
are 30◦ , 45◦ , and 60◦ .1 (In radians, they are π/6, π/4, and π/3.) You should memorize these values for both
degrees and radians:
θ in degrees θ in radians sin θ √
cos θ √
tan θ
◦
30
π/6
3/3
√1/2 √3/2
45◦
π/4
2/2
2/2
√
√1
60◦
π/3
3/2 1/2
3
(Remember that once you know sin and cos, you can get all the trigs.)
TO REMEMBER THIS: I pay attention to the numerators. For sines, the tops go
cosines, the order is reversed!
√
1,
√
2,
√
3. For
Ex 2: If a right triangle has a 30◦ angle, and its adjacent leg is 6, find the lengths of the other two sides.
Basic Applications of Right Triangle Trig
The trig functions can be useful whenever you have a situation with a given angle and a right triangle. The
main thing to keep in mind is: find out WHICH two sides of the triangle interest you (one is known, the other
is the unknown). Once you determine the two sides, write down their trig ratio (usually sin, cos, or tan).
Ex 3: A right triangle has a hypotenuse of 3 and an acute angle of 35 degrees. Determine the area and
perimeter of the triangle.
TO START: To find the adjacent leg, use cos = adj/hyp. For the opposite leg, sin = opp/hyp.
NOTE: Some problems let you type “deg”, as in “sin(35deg)”. Otherwise, you would HAVE to convert to
radians: sin(35pi/180).
Ex 4: The base of a right circular cone has diameter 12 inches. The angle between the radius and the
slanted edge is 45 degrees. Determine the height and volume of the cone.
Ex 5: A radio transmission tower is 33 feet tall and makes a right angle with the ground. A guy wire
(supporting wire) is to be attached to the tower 20 feet from the top of the tower and makes an angle of 39
degrees with the ground. Determine the length of the guy wire.
TO START: Note the angle of 39◦ is made with the ground. That’s how you know which angle to label.
Ex 6 (two triangles): If AD = 5 in the figure on
the right, find the lengths AB and BC.
APPROACH: The top two triangles have a common hypotenuse AE. Find that length first, so that
you have a side of ∆ABE. Similarly, you’ll want to
find BE to get a “link” between the triangles ∆ABE
and ∆BCE.
1 30◦ and 60◦ come from splitting up an equilateral triangle, and 45◦ comes from an isosceles triangle. If you want to know more
about where these angles come from, talk to me outside of class.
Trig Functions of Arbitrary Angles
Note that SOHCAHTOA only works for acute angles. When we want to use trigonometry with ANY angle,
we use this definition instead.
The Trig Functions of Any Angle: Suppose the
angle θ is drawn in standard position. Let (x, y) be a
non-origin point on its terminal side, and let r be its
radius (distance to the origin): r2 = x2 + y 2 . Then
we have
sin(θ) =
cos(θ) =
tan(θ) =
y
r
x
r
y
x
csc(θ) =
sec(θ) =
cot(θ) =
r
y
r
x
x
y
x = r cos(θ), y = r sin(θ)
TO REMEMBER THIS: Think of drawing a right triangle where opp = y, adj = x, and hyp = r. When
you make these replacements, these are the same formulas as SOHCAHTOA.
The good news is: every identity we learned in the last class still works with this definition! For instance,
we still have tan = sin / cos and sin2 + cos2 = 1, etc.
Ex 7:
(a) If P (24, −7) is on the terminal side of θ, find sin(θ), cos(θ), and tan(θ).
(b) Do the same steps if P (0, 4), is on the terminal side. (Note: θ is a right angle here!)
Ex 8: Find the exact values of sec(θ) and csc(θ) if θ is in standard position and the terminal side of θ is in
Quadrant IV and on the line 2x + 7y = 0.
OUTLINE OF THE WORK: You’ll want to rewrite the line is a more useful form: y = −2/7x. Next, you
can pick ANY x value for P as long as it is in Quad IV, so it must be positive. I’ll pick x = 7, because it makes
y easy: y = −2, and P is (7, −2).
Ex 9: Find the values of sin(θ) and cot(θ) if θ is in Quad III and its terminal side is perpendicular to
y = −9x + 4.
TO START: Get the slope of the terminal side: m = −1/(−9) = 1/9. Next, terminal sides MUST go through
the origin, so the terminal side is y = 1/9x. Repeat the steps of Ex 8.
Signs of the Trigs
There is a very important connection between the sign of a trig function and the quadrant the angle lies in.
The sign of the trig depends on the signs of x and y, of course. We’ll make a lot of use of this next class.
1. Quad I: All trigs are positive.
2. Quad II: Sin is positive (as is
its reciprocal csc). The others
are negative.
3. Quad III: Tan is positive (as
is cot).
4. Quad IV: Cos is positive (as
is sec).
Handy mnemonic:
S
T
A
C
“A Smart Trig Class”
When you have an angle measurement, we usually first rewrite it as a coterminal value from 0◦ to 360◦ (or
from 0 to 2π). However, if you get a multiple of 90◦ (i.e. of π/2), then your angle is quadrantal and does not
belong to a quadrant!
Ex 10: For each angle, find its quadrant.
(a) 500◦
(b) −5π/3
(c) 17π/4
(d) 17π/2
Ex 11:
(a) If cos(θ) < 0 and sin(θ) > 0, which quadrant is θ in?
(b) If sec(θ) > 0 and tan(θ) < 0, which quadrant is θ in?
Ex 12: For each of these quadrantal angles, find all six values of the trig functions. (Say “NO SOLUTION”
for any undefined values.)
(a) −450◦
(b) 17π
NOTE: For quadrantal angles, exactly two of the trigs are undefined!