Download Section 3.6

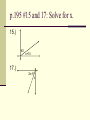
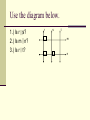
Do Now

Geometry
3.6: Prove Theorems about Perpendicular
Lines
Theorems
 Theorem 3.8: If two lines intersect to form a
linear pair of congruent angles, then the lines
are perpendicular.
1
2
 Theorem 3.9: If two lines are perpendicular,
then they intersect to form 4 right angles.
1
3
2
4
Theorems
 Theorem 3.10: If two sides of two adjacent
acute angles are perpendicular, then the
angles are complementary.
1
2
Theorems
 Theorem 3.11: If a transversal is
perpendicular to one of two parallel lines,
then it is perpendicular to the other.
 Theorem 3.12: In a plane, if two lines are
perpendicular to the same line, then they are
parallel to each other.
p.195 #15 and 17: Solve for x.
15.)
63
x+14
17.)
2x–9
x
Use the diagram below.
1.) Is r s?
2.) Is m n?
3.) Is r t?
r
s
t
m
n
Homework
 Study Guide for Section 3.6
Chapter 3 Test (3.1-3.6)
 3.1: Vocabulary


Parallel, skew, perpendicular
Alt. Int, Alt. Ext, Corresponding, Consec. Int.
 3.2: Parallel Lines


Alt. Int. angles, Alt. Ext. angles, and
Corresponding angles are congruent.
Consec. Int. angles are supplementary.
 3.3: Determine if lines are parallel

Converse of theorems
Chapter 3 Test (3.1-3.6)
 3.4: Slope- Determine if lines are parallel,
perpendicular, or neither.


Parallel lines: same slope
Perpendicular lines: slopes are negative reciprocals
 3.5: Lines


Graphing
Write equation of lines using either:



y = mx + b
y – y1 = m(x – x1)
Write equations of lines parallel or perp. to other
lines given graph or equation.
Chapter 3 Test (3.1-3.6)
 3.6: Perpendicular Lines Theorems


Identify if lines are parallel given information.
Solve for x