* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download r 0
Survey
Document related concepts
Transcript
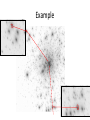
Atmospheric turbulence Eric Gendron Wavefront, and image • The energy (= light rays) propagates orthogonally to the wavefront spherical wavefront convergence point = centre of the sphere no real convergence point non spheric wavefront Aberrations • Difference between the actual wavefront, and the ideal one • Optical path difference varying across the pupil : d(x,y) x d(x,y) no real convergence point aberrated wavefront Aberrations : examples • Astigmatism convergence point (center of curvature) in a vertical plane convergence point (center of curvature) in a horizontal plane • d(x,y) = x2-y2 or d(x,y) = xy • Easily created by tilting a lens in an optical system Aberrations : examples • Spherical rays from pupil edge converge here rays from pupil centre converge here • wavefront curvature changes linearly with pupil radius • d(x,y) = r3 • Any simple lens creates spherical aberration Aberrations : examples • Defocus convergence point (center of curvature) where convergence point was expected • « wrong radius » • d(x,y) = x2+y2 • Easily created by moving a lens along the optical axis Aberrations : examples • Tilt convergence point (center of curvature) where convergence point was expected • « image is not centered » • d(x,y) = x or d(x,y) = y • Easily created by moving a lens transversal to the optical axis When aberrations depend on l • Chromatic blue wave converge here red wave converge here • Chromatic aberration of a single lens – mainly defocus (focal length is shorter at short l) • In general : wavefront shape depends on wavelength ! – can be anything : spherical in the red, and astigm in the blue When aberrations depend on field position • Field curvature – defocus varies quadratically with field angle • Distorsion – tilt is introduced with field angle Diffraction • 2 Image = |electric field in focal plane| • Electric field in focal plane = F ( electric field in pupil plane ) • Phase : (x, y) 2 l d (x, y) • Electric field in the pupil : amplitude A(x, y) exp i ( x,y ) phase Diffraction limit • For a « perfect » wavefront : the image is determined only by the pupil function of the instrument (assuming uniform amplitude) |F [A(x,y)] |2 Diffraction limit • For a circular aperture : Airy pattern 2 2J1 () I( ) l D R lf angle distance R in the focal plane normalized intensity D FWHM l D 0 = 1.22 l/D R0 = 1.22 lf/D (or R) Aberrations • With f(x,y)≠0 – image becomes wider than l/D, light is spread around – peak intensity is reduced • Relation between image quality and phase ? • How to measure image quality ? Image formation depends on l F • Image(u,v) = | 2id (x,y ) [ A(x, y) e l ] |2 • Same wavefront d(x,y), but different images : l=1 µm l=0.7 µm l=0.5 µm Phase variance • The phase variance tells how degraded the wavefront is : 1 2 2 s S pupil (x, y) dx dy • sf2=0 when the wavefront has no aberration • units : radians2 • proportional to l-2 f(x,y) 2 l s 2 (l1) s 2 (l 2 ) 2 l1 s2 (l1) l12 s 2 (l 2 ) l22 constant • will allow us to transform quantities in terms of wavelength x Strehl ratio • Ratio between – the intensity of the degraded image on the optical axis – the intensity of the diffraction-limited image on the optical axis 0 ≤ SR ≤ 1 SR>1 impossible !!! Idiff Ideg SR Idiff Ideg Phase variance and SR • • • • Approximation : SR e Usually ≈ok for sf2< 1 rd2 True when phase is a white noise Exercice : s 2 – SR(0.5µm) = 0.40. Determine SR at 1.65 µm. Atmospheric turbulence • Turbulence is not sufficient to produce wavefront distorsion – wavefront is distorted because of random refractive index fluctuations • Temperature fluctuations are required (and/or water vapor concentration fluctuations) cold air warm air Atmospheric turbulence • Air refractive index depends on wavelength • Air refractive index depends on temperature air refractive index 0°C 20°C wavelength • optical path fluctuations are, at first order, independent of wavelength : wavefront shape d(x,y) is close to achromatic Atmospheric turbulence • Turbulent temperature mixing occurs mainly – close to the ground (0-40m) – at inversion layer (1-2 km) – at jet-stream level (8-12 km) • Most of it occurs at interface between air slabs – notion of « turbulent layers » Atmospheric turbulence • Fractal properties • Change of spatial scale turns into amplitude factor • comes from Kolmogorov statistics (1941) : – statistical scale invariance of the cascade : sc aling arguments and dimensional analysis – ,b? V = speed e = energy V e Lb V e1/ 3 L1/ 3 L = distance Atmospheric turbulence • 3-D phase structure function of refractive index : (n(x) n(x r)) 2 • True for l0 < r < L 0 Dn (r) CN2 r 2 / 3 : the inertial regime – inner scale l0 – outer scale L0 • CN2 is called refractive index structure constant – depends on altitude h : CN2(h) – is expressed in m-2/3 • Phase variance will vary proportionally to CN2(h) Atmospheric turbulence • 3-D phase structure function of refractive index : (n(x) n(x r)) 2 • True for l0 < r < L0 Dn (r) CN2 r 2 / 3 : the inertial regime – inner scale l0 – outer scale L0 • CN2 is called refractive index structure constant – depends on altitude h : CN2(h) – is expressed in m-2/3 kolmogorov L0=100m • 3D power spectrum : 0.033CN2 W (k) k11/ 3 W (k) 0.033CN2 (k 2 ) 2 11/ 6 0 L Von Karman version Von Karman L0=10m Wavefront statistics • 2D phase power spectrum : Wiener spectrum Wf (k) 0.023 r05 / 3 k11/ 3 • 2D phase structure function (x) (x r) ( ) 2 5/3 r D (r) 6.88 r0 • r0 characterizes the amplitude of wavefront disturbance The Fried parameter • Fried, JOSA, 1966 : • r0 is the diameter of a diffraction-limited telescope having the same resolution as an infinitely large telescope limited by the atmosphere turbulence large telescope, limited by the atmosphere diameter r0 same resolution l/r0 image width The Fried parameter seeing-limited telescope diffraction-limited telescope l/r0 l/D r0 • When D<r0 : the telescope is limited by diffraction – wavefront is « nearly flat » over the aperture • When D>r0 : the telescope is seeing-limited • r0 : area over which the wavefront can be considered as « flat » – with respect to l ! telescope diameter D Order of magnitude of r0 ??... In the visible Exceptionally : Astronomical site : Meudon : Horizontal propag : 25 cm 10 cm 3 cm ~ mm The Fried parameter • Expression of r0 : • Notice that • For a fully developped Kolmogorov turbulence : 3 / 5 2 2 1 2 r0 0.423 CN (h) l cos r0 l6 / 5 5/3 D 2 s 1.03 r0 – sounds like a definition : r0 =area over which phase variance ≈ 1 rd2 • Seeing : seeing 0.976 l r0 seeing l r0 seeing l1/ 5 Image properties • typical atmospheric-degraded image : – structure with speckles (short exposures) • Typ. size of a speckle – l/D • Typ. size of long exposure image – l/r0 seeing = l/r0 l/D Long-exposure optical transfer function • One demonstrate that the long-exposure transfer function is the product between – the OTF of the telescope – an OTF specific to atmosphere H(u) H tel (u) e 1 D (u) 2 H(u) spatial frequency u r0/l D/l Exercice • On a 1m telescope, seeing is 3 arcsec at lvis=0.5µm. SR at l=10 µm ? • • • • 3 arcsec = 1.45e-5 rd =lvis/r0 : r0(0.5µm)=3.4cm sf2=1.03(D/r0)5/3 = 283 rd2 at lvis=0.5µm sf2(0.5µm) 0.52 = sf2(10µm) 102 => sf2(10µm) = 0.71 rd2 SR = exp(-0.71) = 0.49 • or ... scale r0 – r0(10µm) = r0(0.5µm) (10/0.5)6/5 = 1.25m – sf2(10µm) = 1.03(D/r0)5/3 = 0.71 rd2 Temporal evolution • One assumes that the layers move as a whole, with speed of inner eddies slower than the global motion (Taylor hypothesis) • One define a correlation time : – V is the average speed 3/5 CN2 (h)v(h) 5 / 3 dh V 2 C N (h) dh • t0 is proportional to l6/5 t 0 0.31 r0 V Angular anisoplanatism • isoplanatic : when wavefronts are the same for the different directions in the field • If separated enough, 2 points of the field will see different wavefronts directn 1 directn 2 r • One defines q0 0.31 0 H is the average height H hB 3/5 CN2 (h) h 5 / 3 dh H 2 CN (h) dh hA • q0 is proportional to l6/5 telescope pupil Example Modal decomposition of phase • f(x,y,t) not easy to handle • Decomposition on a modal basis (x, y,t) ai (t) Z i (x, y) i1 • Zernike modes – – – – – – – defined on a circular aperture analytic expression 1 orthogonal basis Z i (x, y) Z j (x, y) dx dy d ij S pupil look like first order optical aberrations derivatives can be expressed as a simple combination of themselves Fourier transform has analytic expression coefficient ai 1 ai Zi (x, y) (x, y) dx dy S pupil Zernike modes m=0 m=1 n=1 n=2 m=2 • Index i refers to n and m, radial and azimutal orders of the polynomial • i is increasing with n and m, i.e. with spatial frequency m 0 Z i even (r,q ) 2(n 1) Rnm (r) cos(mq ) m 0 Z i odd (r,q ) 2(n 1) Rnm (r) sin( mq ) m 0 Z i (r,q ) n 1 Rn0 (r) R (r) m n (n m )/ 2 s0 1s (n s)! r n 2s s! ((n m) /2 s)! ((n m) /2 s)! Modal decomposition of phase • Phase variance s ai2 2 i1 • Setting one of the ai=0 – best wayto flatten the wavefront Modal spectrum • Noll, R.J., JOSA 66, (1976) tip and tilt low spatial freq high spatial freq (x, y,t) ai (t) Z i (x, y) i1 5/3 D 2 ai c i r0 Residual error • Phase error after perfect compensation of J Zernike modes J iJ 1 ai2 5/3 J 0.257 J 5 / 6 D r0 • Equivalence Zernike deformable mirror with Na actuators – Greenwood, JOSA, 69, 1979 5/3 s 0.27 N a 2 5 / 6 D r0 Residual error • Re-writing Greenwood formula 5/3 5 / 6 D 2 s 0.27 N a r0 5/3 D /n a 2 s 0.335 r 0 na actu across the diameter Na 4 n a2 Na actuators inside the pupil • sf2 will be kept constant if one keeps product (r0 na) constant Temporal spectrum log(PSD) tip-tilt f-2/3 f0 higher orders Power Spectral Density • Temporal spectrum of ai(t) f-17/3 frequency (hz) log(f) fc f c 0.3(n 1) V D f-11/3 Angular correlations ai (0) ai (q ) ai2 normalized correlation tip-tilt high-order mode D (n 1)H low order mode separation angle Thanks for your attention