Download 1. A weightlifter is raising a 100 kg barbell above his head at

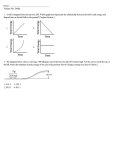
1. A weightlifter is raising a 100 kg barbell above his head at constant velocity. What force is he applying to the barbell?
2. A weightlifter is holding a 100 kg barbell above his head. What force is he applying to the barbell?
Work
Energy is the ability to do work, but what is work?
3. A force of 14 N is applied to a 2 kg mass over a distance of 6 meters. What work is done on the mass?
4. Ten Joules of work are used to push a box for 2 meters. What force was applied to the box?
5. A weightlifter lifts a 100 kg barbell 2 m above the ground. a. What force did he overcome to lift the barbell?
b. How much work did he do?
How does a lever work?
6. How much work is required to lift a 60 N object 2 meters?
Would it be possible to do the same work by only applying a 20 N force? How?
This is how levers and pulleys allow people to lift heavier loads than they would normally be able to.
https://www.brainpop.com/science/motionsforcesandtime/work/
Work at an angle
7. A little boy pulls a wagon with a force of 10 N at an angle of 30 degrees from the horizontal. If he pulls for 20 meters, how much work does he do?
8. A 10 kg crate is pulled 20 m across the floor by a rope making a 25 degree angle with the floor. A force of 200 N is applied to the rope and it takes 10 seconds for the crate to move across the floor. How much work is done?
9. As shown in the diagram, a 2 kg box is lifted up the stairs from point A to point B.
a. In what direction is the force one must apply to lift the box?
b. Which distance do you think you use? Calculate the work in lifting the box.
10. A 2 kg book is lifted from the floor to the top of a 1.2 meter tall table. What is the change in energy of the book?
11. A student does 60 J of work to lift a 20 N box. Through what distance did he lift the box?
12. Work is being done when a force:
(1) acts vertically on a cart that can only move horizontally
(2) is exerted by one team in a tug of war when there is no movement
(3) is exerted while pulling a wagon up a hill
(4) of gravitational attraction acts on a person standing on the surface of the Earth
13. An ant carries a 0.05 kg pebble up to the 10th floor, 30 m above the ground. a. How much work does the ant do?
b. How high would you have to lift a 0.8 kg textbook to do the same work?
Power
14. A toy car is pushed at a constant velocity by a force of 6 N across a 9 meter floor. The car crosses this distance in 3 seconds. How much power was used to push the car?
15. A motor is capable of performing 200 J of work every 12 seconds. What power does it generate?
16. A boat weighing 900 N requires a horizontal force of 600 N to move it across the water at 15 m/s. How much power must be provided by the boat’s engine?
17. A 3 kg block is initially at rest on a frictionless horizontal surface. The block is moved 8 meters in 2 seconds by the application of a 12 newtons. What is the average power developed while moving the block?
18. A 1500 W engine lifts a box for 30 seconds. How much work did the engine do? 19. What amount of force must be applied to an object if 200 J of work is done moving it 0.5 m?
20. A 70 kg cyclist develops 210 watts of power while pedaling at a constant velocity of 7 meters per second. What average force is exerted eastward on the bicycle to maintain this constant speed?
21. How much work is done on a skier who applies an average braking force of 9.8 x 102 N and comes to a stop in 10 meters?
22. A student does 60 joules of work pushing a 3 kilogram box up the length of a ramp that is 5 meters long. What is the magnitude of the force applied to the box to do this work?
23. A 5 kg wooden block slides 12 meters across a wooden surface
a. Calculate the force of friction acting on the block
b. Calculate the amount of work done by friction as the block crosses the surface
24. A 70 N steel box is dragged across a steel floor at 15 m/s.
a. Calculate the force of friction acting on the box
b. Calculate the power required to pull this box.
25. How much work can be completed by a 1200­watt motor in 5 minutes?
26. A small electric motor is used to lift a 0.50 kg mass at constant speed. If the mass is lifted a vertical distance of 1.5 meters in 5 seconds, what is the average power developed by the motor?
27. How much work is required to lift a 10­newton weight from 4.0 meters to 40 meters above the surface of Earth?
28. A 40 kilogram boy is traveling around a carousel with radius 0.5 meters at a constant speed of 1.7 meters per second. Calculate his centripetal acceleration.
29. What would happen to his acceleration if his speed were half?
Energy – The ability to do work
Kinetic Energy
Units Potential Energy
Gravitational Potential Energy – if not specified, potential energy is gravitational potential energy
Elastic (or Spring) Potential Energy
Mechanical Energy
30. What is the kinetic energy for a 2 kg toy car traveling at 3 m/s?
31. What is the potential energy of the same toy car if it is atop a 1.2 m table?
32. Calculate the total mechanical energy of the car from #1­2.
33. A spring with spring constant 220 N/m is compressed 0.05 m. What is the energy stored in the spring?
34. A 1200 kg car has kinetic energy of 240,000 J. How fast is it moving?
Work­Energy Theorem
35. 1200 Joules of work are done to a Joey’s 100 kg motorcycle. What is its change in total energy?
36. Monica pulls on a 6 kg toy wagon with a force of 20 N for 2 meters. What is the change in energy of the wagon?
37. Ross does 800 Joules of work pushing a 100 N box up a hill with constant speed. a. What type of energy is Ross giving the box? How much?
b. How high up the hill did he push the box?
38. Phoebe does 500 Joules of work pushing a 20 kg box on a horizontal, frictionless surface.
a. What type of energy is Phoebe giving the box? How much?
b. How fast is the box moving when she is done?
39. What happens to KE when speed doubles? 40. What happens to PE when height doubles?
41. What happens to PEs when x doubles?
When speed is half as much?
When height is half as much?
When x is half as much?
Conservation of Energy – Ideal Systems
http://phet.colorado.edu/en/simulation/energy­skate­park
48. A 1 kg ball released from rest rolls down a hill
a. What type of energy does the ball have initially?
b. When it reaches the bottom of the hill, what will the potential energy be?
c. What type of energy then will the ball have at the bottom of the hill?
49. A marble launcher uses a spring to launch a marble. The spring has spring constant
k = 6000 N/m, and a 0.1 kg marble is sitting on the spring compressed to 0.02 m.
(a) What type of energy does the marble initially have? How much?
(b) Immediately after it is released, what type of energy does the marble have? How much?
(c) At its maximum height, what type of energy does the marble have? How much?
(d) Find the speed of the marble from part (b)
(e) Find the maximum height the marble reaches in part (c)
(f) At half the maximum height, what will the potential energy be? What will the kinetic energy be?
50. A 3.0­kilogram object is placed on a frictionless track at point A and released from rest. (Assume the gravitational potential energy of the system to be zero at point C.)
a. Calculate the gravitational potential energy of the object at point A. b. Calculate the kinetic energy of the object at point B
c. Which letter represents the farthest point on the track the object will reach?
51. A 0.15 kg marble rolls on a frictionless track starting from a height h = 0.39 m. The ball is released from rest at point A.
a. Calculate the KE and PE at point A
b. Calculate the KE and PE at point B
Calculate the KE and PE at point C. How fast is the marble moving at point C?
52. A 1.00­kilogram ball is dropped from the top of a building. Just before striking the ground, the ball’s speed is 12.0 meters per second. What was the ball’s gravitational potential energy, relative to the ground, at the instant it was dropped? [Neglect friction.]
53. A 0.50­kilogram ball is thrown vertically upward with an initial kinetic energy of 25 joules. Approximately how high will the ball rise? [Neglect air resistance.]
54. As a ball falls freely (without friction) toward the ground, its total mechanical energy
1. decreases
2. increases
3. remains the same
Conservation of Energy – Non­ideal Systems
Ideal
Non­ideal
Total Energy Internal Energy http://phet.colorado.edu/en/simulation/energy­skate­park
55. A 1 kg ball released from rest rolls down a 20 m tall hill. Mechanical energy is not conserved
a. What type of energy does the ball initially have? How much?
b. The ball’s speed at the bottom is 10 m/s. Calculate the KE at the bottom.
c. How much energy was lost to heat/friction/internal energy?
56. A 70 kg cliff diver stands atop a 10 m cliff. a. What is his potential energy?
b. His speed when he hits the ground is 10 m/s. What is his KE at the bottom?
c. How much energy was lost to air resistance?
57. A 100 kg motorcycle and rider are traveling at 10 m/s atop a 20 m hill.
a. What is the total mechanical energy at top of the hill (KE + PE)?
b. If 10,000 J are lost to heat, how fast is the motorcycle moving when it reaches the bottom?
Energy Conversions
1. A car is moving along a flat surface with an increasing speed. What type(s) of energy are changing?
2. A car is moving up an incline with constant speed. 3. A car is applying its brakes and slowing down as it moves down a slope. 4. A cart is moving on a flat surface toward a wall and is stopped by a spring on its front.
5. A rocket flies upward with an increasing velocity
58. A student pulls a box 5.0 meters across a horizontal surface at a constant speed of 4.0 meters per second using a force of 60 newtons.
a. Calculate the amount of work done by the student.
b. What type of energy is being produced by this work?
59. A 5.0 kilogram object is dropped from a height of 3.0 meters and hits the ground with a speed of 4.5 meters per second. Determine the amount of work done by friction as the object falls to the ground.
60. A 0.10 newton spring toy with a spring constant of 160 newtons per meter is compressed 0.05 meter before it is launched. When released the spring toy pops up and reaches a maximum height of 1.5 meters.
a. How much elastic potential energy is initially stored in the spring?
b. How much internal energy is produced as the toy springs up to its maximum height?
Momentum and energy in collisions – In a collision…
Momentum is
Total energy is
Mechanical energy is