Download Study Guide for Geo MT Answer Key

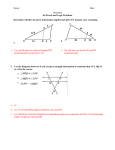
Study Guide for Geometry Mid-Term
What are the three undefined terms in geometry?
__point____
______line_________
____plane_________
The four triangle congruency postulates are: (list them here)
___SSS___
___ASA____
__AAS_____
___SAS___
Why could we NOT use SAS to
prove these triangles to the left
congruent?
The congruent angle pair is not the
included pair. This would be SSA
which is not a congruency postulate
You will need to know the reasons we can justify that triangles are similar. List
them here: __AA_______ ___SAS_______ ____SSS______
Which reason could we use to justify
these triangles similar?
AA. Note that ∠𝐶𝐸𝐷 ≅ ∠𝐴𝐸𝐵
because they are vertical.
Write the similarity statement here:
∆𝐶𝐸𝐷~∆𝐴𝐸𝐵
You will need to know the properties of special quadrilaterals. List them here:
1. Parallelogram: quadrilateral with both pairs of opposite sides congruent
and parallel; opposite angles are congruent; diagonals bisect each other
2. Rectangle: parallelogram with all angles 90 degrees, diagonals are
congruent
3. Rhombus: parallelogram with all sides congruent; diagonals are
perpendicular; diagonals bisect opposite angles
4. Square: rectangle with all sides congruent; rhombus with all angles 90
degrees; has all properties of parallelograms, rhombi and rectangles
You will need to know the formula for finding slope of a line given two points
AND you will need to know how to use to solve problems.
Given two points (𝑥1 , 𝑦1 ) 𝑎𝑛𝑑 (𝑥2 , 𝑦2 )
𝑚=
𝑟𝑖𝑠𝑒 𝑦2 − 𝑦1
=
𝑟𝑢𝑛 𝑥2 − 𝑥1
To find a line parallel to this line, the slope must be the same, but the y-intercept
must be different.
To find a line perpendicular to this line, the slope must be a negative reciprocal
compared to the original slope.
Practice:
Given the points (1, 2) and (-1,-1) write an equation for a line parallel to this line.
Slope is 3/2. A parallel line could be y = 1.5X + 2. Note the y-intercept could be
any number except ½ since that is the intercept of the original line.
Now write the equation of a line perpendicular to this line.
Slope of perpendicular must be -2/3. A perpendicular line could be y = (-2/3)X +1.
Note the y-intercept could be anything.
You will need to know the special triangle segments and points of concurrency
on page 339. You also need to know whether the points of concurrency can occur
on the exterior of a triangle.
Congruence Transformations: page 296
Reflection
translation
rotation
The above terms are all congruence transformations. This means that while the
position of the image may change, the two figures remain congruent.
When two polygons are congruent their corresponding parts are all congruent.
Is dilation a congruence transformation? Why or why not? No it is not because
while the angles remain congruent, the length of the sides may change. This
means that all corresponding parts may no longer be congruent.
Is this dilation an enlargement or a
reduction? This is an enlargement
What is the scale factor?
Scale factor is 2
Is ∆𝐴𝐵𝐶~∆𝐴′𝐵′𝐶′? Yes because the
same scale factor applies
Given that L1 is parallel to L2:
1. Name all pairs of corresponding angles: a & a’ ; b & b’ ; c & c’ ; d & d’
2. Name all pairs of alternate interior angles: c & a’ ; d & b’
3. Name all pairs of alternate exterior angles: b & d’ ; a & c’
What is the difference between the Alternate Interior Angles Theorem and the
Converse of the Alternate Interior Angles Theorem? Alternate Interior Angles
Theorem states that if lines are parallel & cut by a transversal, then alternate
interior angles are congruent. The Converse states that if alternate interior angles
are congruent, then the lines are parallel.
Given that the lines are parallel, which theorem would we use to show that
alternate interior angles are congruent? When we know the lines are parallel we
use the Alternate Interior Angles Theorem to show the angles are congruent.
List all pairs of vertical angles in the diagram above. What is special about ALL
vertical angle pairs? Vertical angles are ALWAYS congruent. Vertical angle pairs
above are: ∠𝑏 ≅ ∠𝑑; ∠𝑏′ ≅ ∠𝑑′; ∠𝑐′ ≅ ∠𝑎′; ∠𝑐 ≅ ∠𝑎
You will need to know the following constructions. Practice in this packet. Bring
questions and concerns to class.
Bisect a Segment page 30
Bisect an Angle page 40
Perpendicular through a point not on the line page 55 bottom of the page
Find X in each of the figures below:
(5𝑥 + 4) + (𝑥 − 2) + (3𝑥 + 7) = 180
9𝑥 + 9 = 180
9𝑥 = 171
𝑥 = 19
𝑥 = 180 − 113
𝑥 = 67
2𝑥 − 45 = 𝑥 + 30
𝑥 − 45 = 30
𝑥 = 75