Download A ∩ B - Gattoni Math

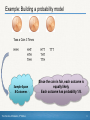
CHAPTER 5
Probability: What Are
the Chances?
5.2
Probability Rules
The Practice of Statistics, 5th Edition
Starnes, Tabor, Yates, Moore
Bedford Freeman Worth Publishers
Probability Models
In Section 5.1, we used simulation to imitate chance behavior.
Fortunately, we don’t have to always rely on simulations to determine
the probability of a particular outcome.
Descriptions of chance behavior contain two parts:
The sample space S of a chance process is the set of all possible
outcomes.
A probability model is a description of some chance process that
consists of two parts:
• a sample space S and
• a probability for each outcome.
The Practice of Statistics, 5th Edition
2
Example: Building a probability model
Toss a Coin 3 Times
HHH
HHT
HTH
THH
Sample Space
8 Outcomes
The Practice of Statistics, 5th Edition
HTT
THT
TTH
TTT
Since the coin is fair, each outcome is
equally likely.
Each outcome has probability 1/8.
3
Probability Models
Probability models allow us to find the probability of any collection of
outcomes.
An event is any collection of outcomes from some chance
process. That is, an event is a subset of the sample space. Events
are usually designated by capital letters, like A, B, C, and so on.
If A is any event, we write its probability as P(A).
In the penny tossing example, suppose we define event A as “2 heads.”
There are 3 outcomes that result in 2 heads.
Since each outcome has probability 1/8, P(A) = 3/8.
Suppose event B is defined as “not 2 heads.” What is P(B)?
P(B) = 1 – 3/8 = 5/8
The Practice of Statistics, 5th Edition
4
Basic Rules of Probability
• The probability of any event is a number between 0 and 1.
• All possible outcomes together must have probabilities whose sum
is exactly 1.
• If all outcomes in the sample space are equally likely, the probability
that event A occurs can be found using the formula
P(A) =
number of outcomes corresponding to event A
total number of outcomes in sample space
• The probability that an event does not occur is 1 minus the
probability that the event does occur.
• If two events have no outcomes in common, the probability that one
or the other occurs is the sum of their individual probabilities.
Two events A and B are mutually exclusive (disjoint) if they
have no outcomes in common and so can never occur together—
that is, if P(A and B ) = 0.
The Practice of Statistics, 5th Edition
5
Basic Rules of Probability
We can summarize the basic probability rules more concisely in
symbolic form.
Basic Probability Rules
•For any event A, 0 ≤ P(A) ≤ 1.
•If S is the sample space in a probability model,
P(S) = 1.
•In the case of equally likely outcomes,
number of outcomes corresponding to event A
P(A) =
total number of outcomes in sample space
•Complement rule: P(AC) = 1 – P(A)
•Addition rule for mutually exclusive events: If A and B are
mutually exclusive,
P(A or B) = P(A) + P(B).
The Practice of Statistics, 5th Edition
6
Two-Way Tables and Probability
When finding probabilities involving two events, a two-way table can
display the sample space in a way that makes probability calculations
easier.
What is the relationship between educational achievement and home
ownership? Find the probability that an adult:
(a) is a high school graduate.
Homeowner
Not
homeowner
Total
HS
graduate
Not HS
graduate
Total
221
119
340
89
71
160
(b) is a high school graduate
and owns a home.
(c) is a high school graduate or
310
190
500
owns a home.
Define events A: is a graduate and B: owns a home.
(b)
(a)We
(c)
We
Each
want
want
student
totofind
find
isP(graduate
P(graduate
equally likely
and
ortohomeowner),
home
be chosen.
owner),
310
that
that
students
is,is,P(A
P(Aorand
are
B). B).
graduates.
There
So,graduates
P(graduate)
and
=“Homeowner”
P(A)
340 homeowners.
= 310/500.
However,
221
Look
at are
the 310
intersection
of the
row and
“graduate”
column.
There
221 graduates
whothem
are homeowners.
So, P(A and
graduates
ownare
homes
– don’t count
twice!
B)
P(A
= 221/500.
or B) = (221 + 89 + 119)/500. So, P(A or B) = 429/178
The Practice of Statistics, 5th Edition
7
General Addition Rule for Two Events
We can’t use the addition rule for mutually exclusive events unless the
events have no outcomes in common.
Event A
Graduate
P(A) = 310/500
A
Outcomes here are
double-counted by
P(A) + P(B)
B
BBBBA
Event B
Homeowner
P(B)= 340/500
Event A and B
Graduate and homeowner
P(A and B) = 221/500
General Addition Rule for Two Events
If A and B are any two events resulting from some chance
process, then
P(A or B) = P(A) + P(B) – P(A and B)
The Practice of Statistics, 5th Edition
8
Venn Diagrams and Probability
Because Venn diagrams have uses in other branches of mathematics,
some standard vocabulary and notation have been developed.
The complement AC contains exactly the outcomes that are not in A.
The events A and B are mutually exclusive (disjoint) because they do not
overlap. That is, they have no outcomes in common.
The Practice of Statistics, 5th Edition
9
Venn Diagrams and Probability
The intersection of events A and B (A ∩ B) is the set of all outcomes
in both events A and B.
The union of events A and B (A ∪ B) is the set of all outcomes in either
event A or B.
Hint: To keep the symbols straight, remember ∪ for union and ∩ for intersection.
The Practice of Statistics, 5th Edition
10
Venn Diagrams and Probability
Homeowner
Not
homeowner
Total
HS
graduate
Not HS
graduate
Total
221
119
340
89
71
160
310
190
500
A
89
221
Recall the example on high school graduates and homeowners. We can
use a Venn diagram to display the information and determine probabilities.
B
119
71
Define events A: graduate and B: homeowner.
Region in Venn diagram
In words
In Symbols
Count
In the intersection of two
circles
Inside Circle A, outside
Circle B
Inside circle B, outside
circle A
Outside of both circles
Graduate and homeowner
A∩B
221
Graduate but not a
homeowner
Homeowner but not a
graduate
Not a graduate or
homeowner
A∩Bc
89
Ac∩B
119
Ac∩Bc
71
The Practice of Statistics, 5th Edition
11