* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PreLecture 18
Center of mass wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Gibbs free energy wikipedia , lookup
Internal energy wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Hunting oscillation wikipedia , lookup
Kinetic energy wikipedia , lookup
Classical central-force problem wikipedia , lookup
Hooke's law wikipedia , lookup
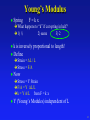
Lecture 18: Elasticity and Oscillations I Simple Harmonic Motion: Definition Springs: Forces Springs: Energy Simple Harmonic Motion: Equations Simple Harmonic Motion Vibrations Vocal cords when singing/speaking String/rubber band Simple Harmonic Motion Restoring force proportional to displacement Springs: F = -kx Springs: Forces Hooke’s Law: The force exerted by a spring is proportional to the distance the spring is stretched or compressed from its relaxed position. FX = -k x Where x is the displacement from the relaxed position and k is the constant of proportionality. relaxed position (equilibrium position) FX = 0 +x x=0 +x Springs: Forces Negative displacement: Positive force Positive acceleration Zero displacement (at equilibrium): Zero force Zero acceleration Positive displacement: Negative force Negative acceleration Springs: Energy Force of spring is Conservative: F = -k x W = ½ k x2 Work done only depends on initial and final position. Potential Energy: Uspring = ½ k x2 U A mass oscillating on a spring: Energy = U + K = constant ½ k x2 + ½ m v2 = total energy 0 m x=0 x x +x Springs: Energy Maximum Negative displacement: Maximum potential energy Zero kinetic energy Zero displacement (at equilibrium): Zero potential energy Maximum kinetic energy Maximum Positive displacement: Maximum potential energy Zero kinetic energy Simple Harmonic Motion x(t) = [A]cos(t) v(t) = -[A]sin(t) a(t) = -[A2]cos(t) xmax = A vmax = A amax = A2 x(t) = [A]sin(t) OR v(t) = [A]cos(t) a(t) = -[A2]sin(t) Period = T (seconds per cycle) Frequency = f = 1/T (cycles per second) Angular frequency = = 2f = 2/T For spring: 2 = k/m Spring Example A mass of m = 4 kg is attached to a spring with k = 16 N/m and oscillates with an amplitude A = 0.15 m. What is the magnitude of the acceleration of the mass when the potential energy stored in the spring is equal to the kinetic energy of the mass? First, use energy to find x where U = K: » U + K = constant Second, use Hooke’s Law to find force on the mass: » F = -k x Third, use Newton’s Second Law to find acceleration of mass: » F=ma Spring Example A mass of m = 4 kg is attached to a spring with k = 16 N/m and oscillates with an amplitude A = 0.15 m. What is the magnitude of the acceleration of the mass when the potential energy stored in the spring is equal to the kinetic energy of the mass? First, use energy to find x where U = K: » » » » » U + K = constant U + K = ½ k A2 U + U = ½ k A2 k x2 = ½ k A 2 x2 = ½ A2 1 2 x A 2 (since total energy is ½ k A2) (since K = U when they are equal) (since U = ½ k x2 when they are equal) (simplify) = 0.106 m Spring Example A mass of m = 4 kg is attached to a spring with k = 16 N/m and oscillates with an amplitude A = 0.15 m. What is the magnitude of the acceleration of the mass when the potential energy stored in the spring is equal to the kinetic energy of the mass? Second, use Hooke’s Law to find force on the mass: » F=kx (we are only concerned with magnitude) 1 2 F k A 2 = 1.70 N Spring Example A mass of m = 4 kg is attached to a spring with k = 16 N/m and oscillates with an amplitude A = 0.15 m. What is the magnitude of the acceleration of the mass when the potential energy stored in the spring is equal to the kinetic energy of the mass? Third, use Newton’s Second Law to find acceleration of mass: » F=ma (we are only concerned with magnitude) k 1 2 a A = 0.424 m/s2 m 2 Young’s Modulus Spring F=kx What happens to “k” if cut spring in half? 1) ½ 2) same 3) 2 k is inversely proportional to length! Define Strain = DL / L Stress = F/A Now Stress = Y Strain F/A = Y DL/L k = Y A/L from F = k x Y (Young’s Modules) independent of L 15 What does moving in a circle have to do with moving back & forth in a straight line ?? x = R cos = R cos (t) since = t x x 1 1 2 R 8 R 3 Movie 2 8 7 3 y 7 4 6 5 0 -R 2 4 3 2 6 5 46 (A) (B) (C) (A) (B) (C)