Download 3379 Homework 3

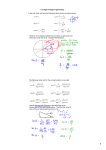
3379 Homework 3
Name
This is a 100 point assignment. Each problem is worth 10 points.
It is due the evening of the midsemester.
1.
Prove or find a counterexample:
In Hyperbolic geometry, the interior angles of an equilateral triangle each
measure 60 degrees.
2.
Let IA be the sum of the measures of the interior angles of a triangle in
Hyperbolic geometry.
The defect of a triangle is 180 IA.
The area of a triangle in Hyperbolic triangle is the product of a given scaling
factor k and the defect of a triangle.
Angle ABC
Disk
Theta = 44.8°
A: (-1.08, 0.31)
Angle BCA
C: (-1.51, 1.84)
C
B: (-2.21, 0.94)
Theta = 30.7°
P-Disk Center: (-1.42, 1.08)
P-Disk Radius: (-0.24, 0.42)
P-Disk Center
B
Angle CAB
Theta = 22.7°
A
P-Disk Radius
Using a scaling factor of k = .547
What is the area of triangle ABC?
3.
Review the proof of the Exterior Angle Theorem below.
Why is this theorem true in Hyperbolic geometry? And in Euclidean?
Write a brief paragraph or two comparing the situation for external angles in
Euclidean, Spherical, and Hyperbolic geometries. Note that things are
different in SG!
Exterior Angle Theorem
An exterior angle of a triangle is greater than either remote interior angle.
( Book 1, Proposition 16 in Elements)
Proof
Using the labels on the adjacent sketch, note that  CBH is an exterior angle of
ABC. We will prove that m CBH > m C.
C
G
D
A
B
H
Choose point D on side CB so that D is the midpoint of the segment. This ensures
that CD  DB. Construct ray AD and choose point G on the ray so that AD  DG.
Thus  ADC  BDG and
ADC  BDG.
The exterior angle  CBH can be decomposed into adjacent angles  CBG and 
GBH. In formula form, then:
m  CBH = m CBG + m  GBH.
If a number can be written as the sum of two positive numbers, then the number is
larger than either summand.
Thus m CBD > m  CBG = m C. QED
Your work:
4.
Supply the reasons and discuss briefly why this proof is true in Euclidean,
Spherical, and Hyperbolic geometries.
If the legs of a biperpendicular quadrilateral are unequal, then the
summit angles are unequal and the larger angle is opposite the longer
leg.
A reminder: An arbitrary biperpendicular quadrilateral has a base with legs
that are perpendicular to it, but the legs are not necessarily congruent. This
is not a Saccheri Quadrilateral
C
angle 3
D
angle 1
m ABC = 90°
A
angle 2 E
m DAB = 90°
B
A.
Let ABCD be a biperpendicular quadrilateral
with base AB and, WLOG, CB > AD.
B.
Choose point E on CB so that BE = AD.
C.
ABED is a Saccheri Quadrilateral.
D.
m1 = m2
E.
Since ADC = 1 +  3,
mADC > m1.
F.
Therefore, mADC > m2.
m2 > m C.
G.
Thus mADC > mC. 
5. Prove or find a counterexample:
The Pythagorean Theorem is true in Euclidean geometry only.
6.
Prove the following:
If the summit angles of an arbitrary biperpendicular quadrilateral are
unequal,
Then the legs are unequal in length and the longer leg is opposite the larger
angle.
Hints:
Use the same sketch as in Problem 4 and
“let ABCD be a biperpendicular quadrilateral with mD > mC”
Problem 7
In Spherical Geometry:
Given a unit sphere and line AB on the sphere. If point C is between A and B,
where is point C. Sketch the situation and discuss the problems with the notion of
between.
In Euclidean and Hyperbolic Geometries, does this problem exist?
Problem 8
Prove this theorem in such a way that you know it is true in Euclidean, Spherical,
and Hyperbolic geometries.
The line segment joining the midpoints of the base and summit of a Saccheri
Quadrilateral is perpendicular to both of them.
Problem 9
Use GSP to show that, in Hyperbolic geometry, sensed parallel lines are not
everywhere equidistant. It’s only in EG, that parallel lines are everywhere
equidistant.
10. Sketch at least 3 Saccheri Quadrilaterals and compare the lengths of the
summit and the base. AB is the base, BC is the right leg.
Here are point coordinates for three of them in the disc centered at the
origin with radius two:
SQ1 A = (-1.09, .21), B = (1.09, .21), C = (1.3, 1.02), D = (-1.3, 1.02)
SQ2 A = (-.39, -.54), B = (.39, -.54), C = (.98, 1.05), D = (-.98, 1.15)
SQ3 A = (-.84, -.38), B = (.84, -.38), C = (-1.49, .76), D = (1.49, .76)
Make a conjecture about the situation with respect to base length and
summit length and begin to draft a proof; what kinds of facts do you think
you’ll need…what kind of proof would you choose…outline your thoughts.