Download The sides of a right triangle

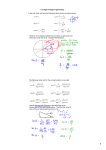
Right Triangle Trigonometry
1
The sides of a right triangle
Take a look at the right triangle, with an acute angle, , in
the figure below.
Side opposite 
Notice how the three sides are labeled in reference to .

Side adjacent to 
In this section, we will be studying special ratios of the
sides of a right triangle, with respect to angle, .
2
These ratios are better known as our
six basic trig functions:
3
Definitions of the Six Trigonometric Functions
opposite
sin  
hypotenuse
adjacent
cos  
hypotenuse
opposite
tan =
adjacent
hypotenuse
csc  
opposite
hypotenuse
sec  
adjacent
adjacent
cot =
opposite
4
Definitions of the Six Trigonometric Functions
To remember the definitions of sine, cosine and tangent,
we use the acronym :
“SOH CAH TOA”
O
A
O
S
C
T
H
H
A
5
Example
Find the exact value of the six trig functions of  in the triangle
below:
5

First find the length of the hypotenuse using
the Pythagorean Theorem.
9
6
Example
12
Given that  is an acute angle and cos  
, find the
13
exact value of the five remaining trig functions of .
7
Example
Find the value of sin  given cot  = 0.387, where  is an
acute angle. (Divide ratio and give answer to three significant
digits.)
8
Special Right Triangles
The 45º- 45º- 90º Triangle
Ratio of the sides:
Find the exact values & decimal approximations
(to 3 sig digits) of the six trig functions for 45
45º
2
1
45º
1
sin 45 =
≈
csc 45 =
≈
cos 45 =
≈
sec 45 =
≈
tan 45 =
cot 45 =
9
Special Right Triangles
The 30º- 60º- 90º Triangle
Ratio of the sides:
Find the exact values & decimal approximations
(to 3 sig digits) of the six trig functions for 30
30º
2
3
sin 30 =
csc 30 =
60º
1
cos 30 =
≈
sec 30 =
≈
tan 30 =
≈
cot 30 =
≈
10
Special Right Triangles
The 30º- 60º- 90º Triangle
Ratio of the sides:
Find the exact values & decimal approximations
(to 3 sig digits) of the six trig functions for 60
30º
2
3
sin 60 =
≈
csc 60 =
≈
60º
1
cos 60 =
tan 60 =
sec 60 =
≈
cot 60 =
≈
11
12
Using the Calculator to Evaluate Trig Functions
To evaluate trig functions of acute angles other than 30, 45, and 60,
you will use the calculator.
Your calculator has keys marked , , and .
**Make sure the MODE is set to the correct unit of angle measure.
(Degree vs. Radian)
Example:
Find tan  46.2 to two decimal places.
13
1
Angles and Accuracy of Trigonometric Functions
Measurement of Angle to
Nearest
Accuracy of Trig Function
1°
2 significant digits
0. 1° or 10'
3 significant digits
0. 01° or 1'
4 significant digits
14
Using the Calculator to Evaluate Trig Functions
To find the values of the remaining three functions (cosecant,
secant, and tangent), use the reciprocal identities.
For reciprocal functions, you may use the  button, but DO
NOT USE THE INVERSE FUNCTIONS (e.g. SIN-1 )!
X
Example:
1. Find
csc73.2
(to 3 significant dig)
2. Find cot
11.56
(to 4 significant dig)
15
The Inverse Trigonometric Functions
The inverse trig functions give the measure of the angle
if we know the value of the function.
Notation:
The inverse sine function is denoted as sin-1x or arcsin x.
It means “the angle whose sine is x”.
The inverse cosine function is denoted as cos-1x or arccos x.
It means “the angle whose cosine is x”.
The inverse tangent function is denoted as tan-1x or arctan x.
It means “the angle whose tangent is x”.
16
Example of Inverse Trig Function
1
For example,sin   will yield the acute angle whose sine is 1 .
2
2
1
1
You can think of this as the related equation sin  
2
17
Examples using common angles
Evaluate the following inverse trig functions using the special
triangles (you do not need a calculator):
1)
tan
1
3
2)
cos
1
1
2
18
Examples using the calculator
Evaluate the following inverse trig functions using the
calculator. Give answer in degrees. Round appropriately.
1. tan 1 1.372
2. sin 1  0.64
19
Examples using the calculator
Evaluate the following inverse trig functions using the
calculator. Give answer in degrees. Round appropriately.
3. tan 1 1
4. cos1  0.541
20
Using Trig Ratios to Find Missing Parts of
Right Triangles
Example:
Solve for y in the right triangle below:
52º
9.6
y
Solution:
Since you are looking for the side adjacent
to 52º and are given the hypotenuse, you
could use the _____________ function.
21
Solving Right Triangles
To solve a right triangle is to find any missing angles and
any missing sides.
• You will always be given 3 parts, and you will need to find
3 parts.
• The angles are labeled using capital letters A, B, & C. Use
angle C to represent the right angle. Angles A and B
represent the acute angles.
• The sides are labeled using lowercase letters a, b, & c.
Each side is labeled with respect to its opposite angle.
22
Example
Solve the right triangle with the indicated measures.
1. A  40.7
Solution
a  8.20 in
A= 40.7°
b
c
C
a=8.20”
B
Answers:
B
b
c
23
Example
2. a  25.8 c  35.4
A
c=35.4
b
C
a=25.8
B
Answers:
A
B
b
24
Example
3. Find the altitude of the isosceles triangle below.
36°
36°
8.6 m
25
Example
4. Solve the right triangle with a  8.600 cm
b  11.25 cm
Answers:
A
B
c
26
Angle of Elevation and Angle of Depression
The angle of elevation for a point above a horizontal line
is the angle formed by the horizontal line and the line of
sight of the observer at that point.
The angle of depression for a point below a horizontal line
is the angle formed by the horizontal line and the line of
sight of the observer at that point.
Horizontal line
Angle of
depression
Angle of
elevation
Horizontal line
27
Example
A guy wire of length 108 meters runs from the top of an
antenna to the ground. If the angle of elevation of the top
of the antenna, sighting along the guy wire, is 42.3° then
what is the height of the antenna? Give answer to three
significant digits.
Solution
108 m
h
42.3°
28
29