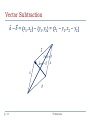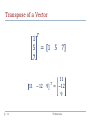Download Slides

Preliminaries of Patter Recognition
K. Ramachandra Murthy
Email: [email protected]
Course Overview

Preliminaries (2 classes)

Introduction to Pattern Recognition (1 class)

Clustering (3 classes)

Dimensionality Reduction
2
– Home work (One Week)

Feature Selection (2 classes)

Feature Extraction (2 classes)
– Assignments (Two Weeks)
Preliminaries
Overview

Linear Algebra

Statistics

Pattern Recognition
3

Patterns and Features

Class information

Classification

Clustering

Dimensionality Reduction
Preliminaries
Linear Algebra
Linear Algebra has become as basic and as applicable
as calculus, and fortunately it is easier.
--Gilbert Strang, MIT
Scalar
A quantity (variable), described by a single real number.
Eg. 24, -98.5, 0.7,….

e.g. Intensity of each digital
Image
5
A pixel
Preliminaries
What is a Vector ?

Think of a vector as a directed line segment in N-dimensions! (has “length”
and “direction”)
𝑎
𝑣= 𝑏
𝑐

Basic idea: convert geometry in higher dimensions into algebra!

Vector becomes a N x 1 matrix!

𝑣 = [a b c]T

Geometry starts to become linear algebra on vectors like 𝑣!
Vector means
a column
vector
y
𝑣
x
6
Preliminaries
Vector
EXAMPLE:
VECTOR=
i.e. A column of numbers
7
Preliminaries
𝑥1
𝑥2
⋮
𝑥𝑛
Parallel Vectors
• Direction is same but length may vary
𝒚
𝒙
𝒙 = 𝒂. 𝒚
𝒚 = 𝒃. 𝒛
𝒛 = 𝒄. 𝒙
𝒛
8
Preliminaries
Vector Addition
𝑎 + 𝑏 = 𝑥1 , 𝑥2 + 𝑦1 , 𝑦2 = 𝑥1 + 𝑦1 , 𝑥2 + 𝑦2
𝑏
𝑎
𝑐
𝑎
𝑎+𝑏 =𝑐
(use the head-to-tail
method to combine vectors)
𝑏
9
Preliminaries
Vector Subtraction
𝑎 − 𝑏 = 𝑥1 , 𝑥2 − 𝑦1 , 𝑦2 = 𝑥1 − 𝑦1 , 𝑥2 − 𝑦2
𝑏
𝑐= 𝑎 + 𝑏
𝑑=𝑎 − 𝑏
𝑎
𝑎
𝑏
10
Preliminaries
Scalar Product
𝑎. 𝑣 = 𝑎. 𝑥1 , 𝑥2 = 𝑎. 𝑥1 , 𝑎. 𝑥2 ;
𝑎. 𝑣
𝑣
𝑎 𝑖𝑠 𝑠𝑐𝑎𝑙𝑟
2. 𝑣
𝑣
𝑣
-𝑣
Change only the length (“scaling”), but keep direction fixed.
Sneak peek: matrix operation (A𝑣) can change length, direction
and also dimensionality!
11
Preliminaries
Transpose of a Vector
1
5
7
11
12
𝑇
= 1 5 7
−12
9
𝑇
11
= −12
9
Preliminaries
Vectors: Dot/Inner Product
• 𝑣. 𝑢= 𝑣 𝑇 𝑢 = 𝑣1
𝑣2
𝑣3
𝑢1
𝑢2 = 𝑣1 𝑢1 +𝑣2 𝑢2 +𝑣3 𝑢3
𝑢3
The inner product is a SCALAR!
•
𝑣
2= 𝑣 𝑇 𝑣
= 𝑣1 𝑣1 +𝑣2 𝑣2 +𝑣3 𝑣3
The length is the dot product
of a vector with itself
• A vector 𝑣 is called unit vector if 𝑣 = 1.
• To make any vector 𝑢, a unit vector divide with it’s
length, i.e.
13
𝑢
𝑢
Preliminaries
Vectors: Dot/Inner Product
The dot product is also related to the angle between the two
vectors
𝑣
𝑣. 𝑢= 𝑣
⟹ cos𝜃 =
𝑢 cos𝜃
𝜃
𝑣. 𝑢
𝑣 𝑢
𝑢
• If 𝑣 and 𝑢 are perpendicular to each other
then 𝑣. 𝑢=0
cos90o =
𝑣
90o
𝑣. 𝑢
𝑣 𝑢
𝑢
⟹ 𝑣. 𝑢 = 0
• If 𝑣 and 𝑢 are parallel to each other
then 𝑣. 𝑢= 𝑣 𝑢
180o
𝑢
𝑣
0o
𝑢
14
Preliminaries
𝑣
Outer Product


Outer product of two vectors is a matrix.
Simple matrix multiplication of vectors
𝑎1
𝑎2 𝑏1
𝑎3
15
𝑏2
𝑎1 𝑏1
𝑏3 = 𝑎2 𝑏1
𝑎3 𝑏1
𝑎1 𝑏2
𝑎2 𝑏2
𝑎3 𝑏2
Preliminaries
𝑎1 𝑏3
𝑎2 𝑏3
𝑎3 𝑏3
Linear Independence


Different direction vectors are independent.
Parallel vectors are dependent
16
Preliminaries
Basis & Orthonormal Bases

Basis (or axes): frame of reference
vs
Basis
2
1
0
−9
1
0
=2.
+ 3. ;
=−9.
+ 6.
3
0
1
6
0
1
4 −1 −9
2 9 2
−1
2
= .
+ .
;
=−3.
+ 3.
7
3 7 1
3
6
3
1
17
Preliminaries
1 0
,
0 1
is a set
of representative for ℝ2
2 −1
,
3
1
is another
Set of representative for ℝ2
Basis & Orthonormal Bases
Basis: a space is totally defined by a set of vectors – any point is
a linear combination of the basis
Ortho-Normal: orthogonal + normal
[Sneak peek: Orthogonal: dot product is zero
Normal: magnitude is one ]
𝑥= 1 0 0
𝑦= 0 1 0
𝑧= 0 0 1
18
𝑇
𝑇
𝑇
𝑥. 𝑦 = 0
𝑥. 𝑧 = 0
𝑦. 𝑧 = 0
Preliminaries
Projection: Using Inner Products
Projection of 𝑥 along the direction 𝑎
y
𝑎. 𝑒
=
𝑎 𝑒
⇒ 𝑎. 𝑒 = 0
⇒ 𝑎. 𝑥 − 𝑝 = 0
⇒ 𝑎. 𝑥 − 𝑡𝑎 = 0
⇒ 𝑎. 𝑥 − 𝑡𝑎. 𝑎 = 0
𝑎. 𝑥
⇒𝑡=
𝑎. 𝑎
cos 900
Light Source
𝑥
𝑒 =𝑥−𝑝
𝑃𝑟𝑜𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑣𝑒𝑐𝑡𝑜𝑟 𝑝 = 𝑡𝑎
𝑎
𝑝 = 𝑡𝑎
x
𝑝=
𝑎𝑇 𝑥
𝑎𝑎𝑇
𝑎 𝑇 = 𝑇
𝑎 𝑎
𝑎 𝑎
Projection Matrix
19
Preliminaries
𝑥
Vectors: Cross Product



20
The cross product of vectors 𝑎 and 𝑏 is a vector 𝑐 which is
perpendicular to 𝑎 and 𝑏
The magnitude of 𝑐 is proportional to the sin of the angle
between 𝑎 and 𝑏
The direction of 𝑐 follows the right hand rule if we are
working in a right-handed coordinate system
Preliminaries
MAGNITUDE OF THE CROSS PRODUCT
𝐴×𝐵 = 𝐴
Example:
2
𝑎= 1 ;
5
𝑖
𝑗
𝑎×𝑏 = 2 1
−3 2
21
𝐵 sin 𝜃
−3
𝑏= 2
7
𝑘
5 = 𝑖 7 − 10 − 𝑗 14 + 15 + 𝑘 4 + 3
7
= −3𝑖 − 29𝑗 + 7𝑘
Preliminaries
What is a Matrix?

A matrix is a set of elements, organized into rows and
columns
rows
columns
22
𝑎11
𝑎21
𝑎12
𝑎22
Preliminaries
Example
 x11 x12 x13 
 x 21 x 22 x 23


 x31 x32 x33
23
Preliminaries
Basic Matrix Operations

Addition, Subtraction, Multiplication: creating new matrices (or functions)
a b   e
c d    g

 
f  a  e b  f 


h  c  g d  h 
a b   e
c d    g

 
f  a  e b  f 


h  c  g d  h 
a b   e
c d   g


f  ae  bg


h  ce  dg
Just add elements
Just subtract elements
af  bh
cf  dh 
Multiply each row by
each column
Note: Matrix multiplication is possible only when number of columns of first
matrix is equal to number of rows of second one.
24
Preliminaries
Matrix Times Matrix
L  MN
l11 l12
l
l
21
22

l31 l32
l13   m11 m12
l23   m21 m22
l33  m31 m32
m13   n11 n12
m23   n21 n22
m33  n31 n32
l12  m11n12  m12 n22  m13 n32
25
Preliminaries
n13 
n23 
n33 
Multiplication

Is AB = BA? Maybe, but maybe not!
a b   e
c d   g



f  ae  bg ...


h   ...
...
e
g

f  a b  ea  fc ...




h   c d   ...
...
Heads up: multiplication is NOT commutative!
26
Preliminaries
Transpose & Symmetric Matrix
Transpose of a matrix A is formed by turning all the rows of a
given matrix into columns and vice-versa.
2
4
3
5
𝑇
2
=
3
4
5
Matrix A is called a symmetric matrix if 𝐴 = 𝐴𝑇
2 3
6
3 10 22
6 22 5
27
Preliminaries
Matrix operating on vectors



Matrix is like a function that transforms the vectors on a plane
Matrix operating on a general point => transforms x- and ycomponents
System of linear equations: matrix is just the bunch of coeffs !
x' = a.x + b.y
y' = c.x + d.y
28
a b   x   x'

    
c d   y   y '
Preliminaries
Linear Transformation
𝑦1 = 𝑎11 𝑥1 + 𝑎12 𝑥2 + ⋯ + 𝑎1𝑛 𝑥𝑛
𝑦2 = 𝑎21 𝑥1 + 𝑎22 𝑥2 + ⋯ + 𝑎2𝑛 𝑥𝑛
𝑦 = 𝐴𝑥 ⟹
⋮
𝑦𝑑 = 𝑎𝑑1 𝑥1 + 𝑎𝑑2 𝑥2 + ⋯ + 𝑎𝑑𝑛 𝑥𝑛
𝑦1
𝑎11
𝑦2
𝑎21
⇔ ⋮ =
⋮
𝑦𝑑
𝑎𝑑1
29
𝑎12
𝑎22
⋮
𝑎𝑑2
… 𝑎1𝑛
… 𝑎2𝑛
⋮
… 𝑎𝑑𝑛
Preliminaries
𝑥1
𝑥2
⋮
𝑥𝑑
Rotation
cos 𝜃
Rotation Matrix = 𝑅 𝜃 =
sin 𝜃
−sin 𝜃
cos 𝜃
𝑥′
𝑦′
• We can rotate any 2-dimensional vector using 𝑅 𝜃
as follows
𝑥′
cos 𝜃
=
𝑦′
sin 𝜃
−sin 𝜃 𝑥
cos 𝜃 𝑦
𝜃
0
1
Example :
cos 90
sin 90
−sin 90 1
0
=
cos 90 0
1
−1 1
0
=
0 0
1
900
30
𝑥
𝑦
Preliminaries
1
0
Rotation
y
𝑥′
𝑦′
𝑥
𝑦
𝜃
x
31
Preliminaries
Rotation
P
P`
32
Preliminaries
Scaling
Scaling Matrix =
𝑟1 0
0 𝑟2
• We can scale any 2-dimensional vector as
follows
𝑟1
𝑥′
= 0
𝑦′
0
𝑟2
𝑥
𝑦
Example :
2 0 3
6
=
0 4 2
8
33
Preliminaries
Scaling
r 0
0 r
34
a.k.a: dilation (r >1),
contraction (r <1)
Preliminaries
Translation
𝑡𝑥
𝑥
𝑃 = 𝑦 + 𝑡 =𝑃+𝑡
𝑦
′
P’
t
ty
y
P
x
35
tx
Preliminaries
Translation
P’
P
36
t
Preliminaries
Shear
• A transformation in which all points along a given line L remain fixed while other
points are shifted parallel to L by a distance proportional to their perpendicular
distance from L.
L
37
Preliminaries
Shear
38
Preliminaries
Shear
Horizontal Shear:
𝑥′
𝑦′
𝑥 + 𝑚𝑦
1 𝑚 𝑥
=
=
𝑦
0 1 𝑦
Vertical Shear:
𝑥′
1
′ =
𝑦
𝑚
39
𝑥
0 𝑥
=
𝑚𝑥 + 𝑦
1 𝑦
Preliminaries
Identity Matrix
Identity (“do nothing”) matrix = unit scaling, no rotation!
1
0
0
40
𝑥
0 0 𝑥
1 0 𝑦 = 𝑦
𝑧
0 1 𝑧
Preliminaries
Inverse of a Matrix

AI = IA = A

Inverse exists only for square matrices that are non-singular

Some matrices have an inverse, such that: AA-1 = I

Inversion is tricky: (ABC)-1 = C-1B-1A-1
Derived from non-commutativity property
1 0 0
I= 0 1 0
0 0 1
41
Preliminaries
Determinant & Trace of a Matrix


Used for inversion
If det(A) = 0, then A has no inverse
𝑎
𝐴=
𝑐
−1
𝐴

𝑏
𝑑
det 𝐴 = 𝑎𝑑 − 𝑏𝑐
1
𝑑
=
𝑎𝑑 − 𝑏𝑐 −𝑐
−𝑏
𝑎
Trace = sum of diagonal elements (a+d)= sum of eigenvalues
42
Preliminaries
Eigenvalues & Eigenvectors

Eigenvectors (for a square mm matrix S)
𝑆𝑣 = 𝜆𝑣
(right) eigenvector
eigenvalue
Example
𝜆𝜖ℝ
𝑣𝜖ℝ𝑚 ≠ 0
𝑆𝑣
𝑣
43
𝜆𝑣
Preliminaries
Eigenvalues & Eigenvectors
In the shear mapping the red arrow changes direction but the blue arrow does not. The
blue arrow is an eigenvector of this shear mapping because it doesn’t change direction, and
since in this example its length is unchanged its eigenvalue is 1.
44
Preliminaries
Computation of Eigenvalues
𝑆𝑣 = 𝜆𝑣 ⟹ (𝑆 − 𝜆𝐼) 𝑣 = 0
First find the eigenvalues 𝜆 and substitute 𝜆 in the above equation to obtain
eigenvectors
𝐹𝑜𝑟 𝑒𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒𝑠 𝑠𝑜𝑙𝑣𝑒, 𝑑𝑒𝑡 𝑆 − 𝜆𝐼 = 0
Example:
0 1
𝐴=
−6 5
𝑑𝑒𝑡
𝐴 − 𝜆𝐼 =
−𝜆
1
−6 5 − 𝜆
−𝜆
1
= −𝜆(5 − 𝜆)+6=(𝜆 − 2)(𝜆 − 3)
−6 5 − 𝜆
𝐸𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒𝑠 𝑎𝑟𝑒 2, 3
45
Preliminaries
Computation of Eigenvectors
(𝑆 − 𝜆𝐼) 𝑣 = 0
𝜆 = 2:
𝑣1
−𝜆𝑣1 + 𝑣2 = 0
0
−𝜆
1
=
⇒
−6𝑣1 + (5 − 𝜆)𝑣2 = 0
0
−6 5 − 𝜆 𝑣2
−2𝑣1 + 𝑣2 = 0
⇒
−6𝑣1 + 3𝑣2 = 0
Both are same
⇒ 2𝑣1 = 𝑣2 ⇒ 𝑣1 = 𝑡, 𝑣2 = 2𝑡; 𝑡 > 0
∴𝑣=
46
𝑡
is a eigenvector
2𝑡
Preliminaries
Computation of Eigenvectors
𝜆 = 3:
𝑣1
−𝜆𝑣1 + 𝑣2 = 0
0
−𝜆
1
=
⇒
𝑣
−6𝑣1 + (5 − 𝜆)𝑣2 = 0
0
−6 5 − 𝜆 2
−3𝑣1 + 𝑣2 = 0
⇒
−6𝑣1 + 2𝑣2 = 0
⇒ 3𝑣1 = 𝑣2 ⇒ 𝑣1 = 𝑡, 𝑣2 = 3𝑡; 𝑡 > 0
𝑡
∴𝑣=
is another eigenvector
3𝑡
47
Preliminaries
Singular Value Decomposition (SVD)


Handy mathematical technique that has application to many
problems
Given any mn matrix A, algorithm to find matrices U, V and W
such that
𝑨𝒎×𝒏 = 𝑼𝒎×𝒏 𝑾𝒎×𝒏 𝑽𝒏×𝒏
𝑻
U and V are orthonormal
W is nn and diagonal
48
Preliminaries
Singular Value Decomposition (SVD)








A
 
 
 

 
 
 
 
U


 w1 0 0 
 0  0 


 0 0 wn 


V





T
 The columns of U are orthonormal eigenvectors of AAT
 The columns of V are orthonormal eigenvectors of ATA,
 S is a diagonal matrix containing the square roots of eigenvalues from U or V in
descending order.
49
Preliminaries
Singular Value Decomposition (SVD)

The wi are called the singular/eigen values of A

If A is singular, some of the wi will be 0

In general rank(A) = number of nonzero wi

SVD is mostly unique.
50
Preliminaries
For more details
Prof. Gilbert Strang’s course videos:
http://ocw.mit.edu/OcwWeb/Mathematics/18-06Spring2005/VideoLectures/index.htm

Online Linear Algebra Tutorials:
http://tutorial.math.lamar.edu/AllBrowsers/2318/2318.as
p

51
Preliminaries