* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Minor arc
History of geometry wikipedia , lookup
Integer triangle wikipedia , lookup
Line (geometry) wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Perceived visual angle wikipedia , lookup
Rational trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Tangent lines to circles wikipedia , lookup
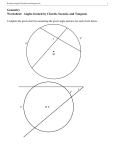
Geometry, Chapter 7 Sections 7.1: Parts of a circle; Central angles; Length of an arc; Area of a sector; Inscribed Angle Theorem 1. Circle – The set of all points in a plane that are a fixed distance from a given point called the center. A circle is named by its center point. arc B • Radius – A segment that joins the center of the circle to a point on the circle. • Chord – A segment that joins two points on a circle. • Diameter – A chord that contains the center of the circle. • Arc – The part of a circle between two points including the two points. • Semicircle - An arc whose endpoints are the endpoints of a diameter. • Major arc: An arc that is longer than a semicircle. Arc ACB is a major arc. • Minor arc: An arc that is shorter than a semicircle. Arc AB is a minor arc. Note: If 2 letters are used to name an arc, it is assumed that the name refers to the minor arc and not the major arc. chord A central angle radius O diameter C semicircle 2. Congruent Circles have congruent radii. Concentric Circles are coplanar circles with a common center. 3. Central Angle of a Circle – An angle whose vertex is the center of the circle and whose sides are radii of the circle. ∠BOC and ∠AOB are examples of central angles. 4. Intercepted Arc of an Angle – The two points of intersection of the angle with the circle and all points of the arc in the interior of the angle. is the intercepted arc of central angle ∠BOC. In the figure above, BC 6. Degree Measure of an Arc (Central Angle Postulate) – In a circle, the degree measure of an arc is equal to the degree measure of the central angle which intercepts it. 7. = Arc-Addition Postulate – If point B lies between points A and C on a circle, then m AB + mBC m ABC . 8. Length of an Arc – Informally, this is the distance between the endpoints of the arc as though it were measured along a straight line. Length of an arc is measured in linear units. Postulate: The ratio of the degree measure m of the arc to 360 (degree measure of the entire circle) is the same as the ratio of the length l of the arc to the circumference. l m m Practice: Find the length of = ⇒ = AB . l ⋅ (2π r ) C 360 360 9. A C 12 in. O l 80° B Sector of a Circle – A region bounded by two radii of a circle and their intercepted arc. • Area of a Sector The ratio of the degree measure m of the central angle of a sector to 360º is the same as the ratio of the area of the sector to the area of the circle. area of sector m = area of circle 360 ⇒ A= m π r2 360 for a circle with radius r. Practice: Find the shaded area in the diagram if m = 60° and the radius is 3 cm. B O mº C Geometry, Chapter 7 B Inscribed Angle – An angle whose vertex is a point on the circle and sides are chords of the circle. 10. D O Inscribed Angle Theorem – The measure of an inscribed angle in a circle is equal to half 1 the measure of its intercepted arc. ∠BCD = BD 11. C 2 A C O Corollary – Inscribed angles that intercept the same arc or congruent arcs are congruent. Here, ∠ABC = ∠ADC 12. B D A B Corollary – An angle is inscribed in a semicircle if and only if it is a right angle. 13. C D O Section 7.2: Perpendicular bisectors of chords; Measures of angles and segments formed by intersecting chords. Theorem: The perpendicular bisector of a chord contains the center of the circle. 1. Corollary: The perpendicular bisectors of any two nonparallel chords intersect at the center of the circle. Using construction techniques and the second theorem, locate the center of the circle. Theorem: 2. C ( 1 Measures of Angles Formed by Intersecting Chords: = ∠1 AC + BD 2 a. b. ) B 1 Measures of Segments formed by Intersecting Chords: (AE)(BE) = (CE)(DE) A E D To show part a. Start with ∠1 = ∠C + ∠B (exterior angle thm 2). Apply Inscribed Angle Thm to ∠C and ∠B. C C B 1 A For part b. Hint: Show ∆AEC ∼ ∆DEB. Then corresponding sides are proportional. E A D B E D Geometry, Chapter 7 Section 7.3: Secant lines and tangent lines; Theorems involving intersecting secants, tangents, and chords 1. Secant Line – A line that intersects a circle (or, in general, any curve) at two points. 2. Tangent Line – A line that intersects a circle at one point. Point of Tangency Tangent line The point of intersection is called a point of tangency. Secant line 3. Theorems for two secants intersecting outside the circle. = E a. ∠ ( 1 AC − BD 2 ) B A 3 1 D 2 b. (AE)(BE) = (CE)(DE) C 4. Theorems for two intersecting tangents. a. = ∠B ( 1 ADC − AEC 2 ) 6. E O b. BA = BC 5. B A C D Theorem for intersecting tangent and secant. ( 1 AC − AD 2 a. ∠ABC = b. BD AB = AB BC B A D ) C Theorems for intersecting tangent and chord. 1 a. ∠ABC = AB 2 C B A b. A radius or diameter of a circle is perpendicular to a tangent line at its point of tangency E Geometry, Chapter 7 Section 7.4: , Constructing incenter, orthocenter, circumcenter, centroid. Constructing an incircle and circumcircle. Constructing a center of a circle. Triangle Inequality. 1. Triangle Centers (a) Incenter – The intersection of the angle bisectors of a triangle. (b) Circumcenter – The intersection of the perpendicular bisectors of the sides of a triangle. (c) Orthocenter – The intersection of the altitudes of a triangle. (d) Centroid – The intersection of the medians of a triangle. Note: The Centroid of a triangle divides the median into segments with ratio 1:2. In other words, the length of the segment from the vertex to the centroid = 2/3 the length of the median. Or, BP = (2/3) BF, AP = (2/3) AE, CP = (2/3) CD. D A 2. B E P F C Construct the circle that passes through the points. These theorems will be helpful when we are solving triangles in Trigonometry with the Law of Sines and the Law of Cosines. 3. Theorem: If two sides of a triangle are not congruent, the angle opposite the longer side is greater than the angle opposite the shorter side. 4. Theorem: If two angles of a triangle are not congruent, the side opposite the larger angle is longer than the side opposite the smaller angle. 5. The Triangle Inequality. In a triangle, the sum of the lengths of any two sides is greater than the third side. B AB + BC > AC AC + BC > AB AB + AC > BC Example: Suppose that AB = 8 cm, BC = 5cm, and AC = 7 cm Order the angles from least to greatest. A C