Download Practice problems on triangle geometry. Problem 1 (a) Describe the

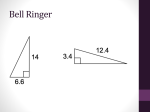
Practice problems on triangle geometry.
Problem 1
(a) Describe the 9 points of the 9-point circle. (You should explain where each of the 9 points is
found in terms of the three vertices and three sides of a triangle.)
(b) Choose any 4 of the 9 points of the 9-point circle and prove that they form a cyclic quadrilateral. (Your proof
should not use the existence of the 9-point circle.)
Problem 2
triangle.
State and prove a theorem that compares the areas of the six triangles cut off by the medians of a
Problem 3
Prove that the orthocenter of an obtuse-angled triangle is an excenter of its orthic triangle.
Problem 4
triangle.
State and prove a theorem that compares the lengths of the bisectors of two unequal angles in a
Problem 5
Let ABC be a triangle with orthocenter H. Prove that the line that joins the midpoint of AH to
the midpoint of AB is perpendicular to the side AC.
Problem 6
(a) Describe four points of a triangle that lie on the Euler line. You should provide the standard
name for each of the four points and give its definition (as an intersection or center).
(b) State and prove a theorem that shows that three of the points that you specified in (a) are collinear.
Problem 7
Prove that every triangle can be inscribed in a circle.
Problem 8
Prove that every triangle has an inscribed circle.
Problem 9
Let ABC be a triangle. Let X, Y, and Z be points on the sides BC, CA, and AB such that AX,
BY , and CZ are the bisectors of the angles of the triangle. You may assume that the lines AX, BY , and CZ are
concurrent at a point I.
Write a, b, and c for the lengths of the sides BC, CA, and AB. The answers calculated in parts (ii), (iii) and (v)
should be expressed in terms of the quantities a, b, and c.
(i) State the angle bisector theorem.
(ii) Apply the angle bisector theorem to find the signed ratios AZ/ZB and BX/XC.
(iii) Consider C as a point on the side BX of triangle ABX. Calculate the signed ratio BC/CX.
(iv) The points C, I, and Z are collinear points on the three sides of triangle ABX. What does Menelaus Theorem
tell us about these points?
(v) Calculate the ratio IX/IA.
Problem 10
State and prove the law of sines.
Problem 11
Let ABC be a triangle. Let EA be the excenter opposite the vertex A, so that EA is the intersection
point of external bisectors of the angles at B and C. Similarly let EB and EC be excenters opposite to the vertices
B and C. Let I be the incenter of triangle ABC.
(a) Prove that I is the orthocenter of triangle EA EB EC .
(b) Deduce that the circumcircle of triangle ABC is the 9-point circle of triangle EA EB EC .
(c) Deduce that the midpoint of IEA lies on the circumcircle of triangle ABC.
Problem 12
Prove that each altitude of a triangle is an angle bisector of the pedal triangle. Give a careful
statement of any theorems that you use in your proof.
Problem 13
Prove that the orthocenter of a triangle is the incenter of its pedal triangle.
Problem 14
(a) Prove that in any triangle, the midpoints of the sides and the feet of the altitudes lie on a circle.
(b) Give a careful statement of all results and theorems that you used in your proof of (a).
Problem 15
Let ABC be a triangle and let Σ be an excircle that touches the segement BC at X (bewteen B
and C) and touches the rays AC and AB at points Y and Z that are outside the triangle.
(a) Prove that AY = AZ, CY = CX, and BZ = BX.
(b) Prove that AY + AZ = AB + BC + CA.
(c) Deduce that the length of AY is the semi-perimeter of triangle ABC.
Problem 16
(i) Prove that the three medians of a triangle are concurrent.
(ii) State and prove a theorem that identifies the location on each median of the centroid of a triangle.
Problem 17
Suppose that ABC is a triangle and that X is a point on the line BC such that AX is a bisector of
the external angle at A of triangle ABC. Prove that BX/XC = -AB/AC.
Problem 18
(i) State and prove the angle bisector theorem.
(ii) Prove that the three angle bisectors of a triangle are concurrent at a point that is equidistant from the three
sides of the triangle.