Download Chapter 6: Mechanical Properties

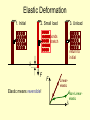
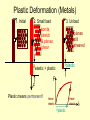
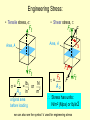
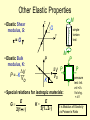
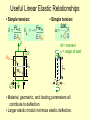
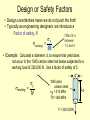
Chapter 6: Behavior Of Material Under Mechanical
Loads = Mechanical Properties.
• Stress and strain:
• What are they and why are they used instead of load and
deformation
• Elastic behavior:
• Recoverable Deformation of small magnitude
• Plastic behavior:
• Permanent deformation We must consider which materials are most
resistant to permanent deformation?
• Toughness and ductility:
• Defining how much energy that a material can take before failure.
How do we measure them?
• Hardness:
• How we measure hardness and its relationship to material strength
Elastic Deformation
1. Initial
2. Small load
3. Unload
bonds
stretch
return to
initial
d
F
F
Linearelastic
Elastic means reversible!
d
Non-Linearelastic
Plastic Deformation (Metals)
1. Initial
2. Small load
bonds
stretch
& planes
shear
delastic + plastic
3. Unload
planes
still
sheared
dplastic
F
F
Plastic means permanent!
linear
elastic
linear
elastic
dplastic
d
Geometric Considerations of the Stress State
The four types of forces act either parallel or perpendicular
to the planar faces of the bodies.
Stress state is a function of the orientations of the planes
upon which the stresses are taken to act.
Engineering Stress:
• Tensile stress, s:
• Shear stress, t:
Ft
Area, A
Area, A
Ft
Ft
lb f
N
= 2 or
s=
2
in
m
Ao
original area
before loading
Ft
F
Fs
Fs
Fs
t=
Ao
F
Ft
 Stress has units:
N/m2 (Mpa) or lbf/in2
we can also see the symbol ‘s’ used for engineering stress
Common States of Stress
• Simple tension: cable
F
F
A o = cross sectional
area (when unloaded)
F
s=
s
Ao
s
• Torsion (a form of shear): drive shaft
M
Ac
M
Fs
Ski lift
(photo courtesy
P.M. Anderson)
Ao
Fs
t =
Ao
2R
Note: t = M/AcR here.
Where M is the “Moment” Ac shaft area & R shaft radius
OTHER COMMON STRESS STATES (1)
• Simple compression:
Ao
Canyon Bridge, Los Alamos, NM
(photo courtesy P.M. Anderson)
Balanced Rock, Arches
National Park
(photo courtesy P.M. Anderson)
F
s=
Ao
Note: compressive
structure member
(s < 0 here).
OTHER COMMON STRESS STATES (2)
• Bi-axial tension:
Pressurized tank
(photo courtesy
P.M. Anderson)
• Hydrostatic compression:
Fish under water
sq > 0
sz > 0
sh< 0
(photo courtesy
P.M. Anderson)
Engineering Strain:
• Tensile strain:
• Lateral strain:
d/2
e = d
Lo
• Shear strain:
wo
dL /2
-dL
eL =
wo
Lo
Here: The Black Outline is
Original, Green is after
application of load
Adapted from Fig. 6.1 (a) and (c), Callister 7e.
q
g = x/y = tan q
x
Strain is always
Dimensionless!
90º - q
y
90º
We often see the symbol ‘e’ used for engineering strain
Stress-Strain: Testing Uses Standardized methods
developed by ASTM for Tensile Tests it is ASTM E8
• Typical tensile test
machine
extensometer
• Typical tensile
specimen
specimen (ASTM A-bar)
Adapted from
Fig. 6.2,
Callister 7e.
gauge
length
Adapted from Fig. 6.3, Callister 7e. (Fig. 6.3 is taken from H.W.
Hayden, W.G. Moffatt, and J. Wulff, The Structure and Properties of
Materials, Vol. III, Mechanical Behavior, p. 2, John Wiley and Sons,
New York, 1965.)
- During Tensile Testing,
Instantaneous load and displacement is measured
LOAD vs. EXTENSION PLOTS
These load / extension graphs depend on the size of the specimen.
E.g. if we carry out a tensile test on a specimen having a cross-sectional area twice
that of another, you will require twice the load to produce the same elongation.
The Force .vs. Displacement plot will be the same shape as the
Eng. Stress vs. Eng. Strain plot
The Engineering Stress - Strain curve
Divided into 2 regions
ELASTIC
PLASTIC
Linear: Elastic Properties
• Modulus of Elasticity, E:
Units:
E: [GPa] or [psi]
(also known as Young's modulus)
• Hooke's Law:
s=Ee
s
F
d/2
Ao
E
wo
e
Linearelastic
Lo
dL /2
Here: The Black
Outline is Original,
Green is after
application of load
Typical Example:
• Problem 6.5:
– Aluminum tensile specimen, square X-Section
(16.5 mm on a side) and 150 mm long
– Pulled in tension to a load of 66700 N
– Experiences elongation of: 0.43 mm
• Determine Young’s Modulus if all the
deformation is recoverable
Solving:
s = F A = 66700 N
=
244.995
MPa
2
-3
0
16.5*10 
e = L L = 0.43mm 125mm = 0.00344
0
Because we are to assume all deformation is
recoverable, Hooke's Law can be assumed:
s = E  e  E = s e = 244.995MPa 0.00344
E = 71219.6 MPa = 71.2 GPa
Poisson's ratio, n
• Poisson's ratio, n:
eL
eL
n=- e
metals: n ~ 0.33
ceramics: n ~ 0.25
polymers: n ~ 0.40
Units:
n: dimensionless
e
-n
–n > 0.50 density increases
–n < 0.50 density decreases
(voids form)
Other Elastic Properties
• Elastic Shear
modulus, G:
t
M
G
t=Gg
• Elastic Bulk
modulus, K:
V
P = -K
Vo
simple
torsion
test
g
M
P
P
K
V P
Vo
• Special relations for isotropic materials:
E
G=
2(1 + n)
E
K=
3(1 - 2n)
P
pressure
test: Init.
vol =Vo.
Vol chg.
= V
E is Modulus of Elasticity
n is Poisson’s Ratio
Looking at Aluminum and the
earlier problem:
G= E
2  1 + n 
= 71.2GPa
2  1 + 0.33HB 
G  26.8GPa
K=E
3  1 - 2n 
K  69.8GPa
= 71.2GPa
3  1 - 2  0.33HB 
Young’s Moduli: Comparison
Metals
Alloys
1200
1000
800
600
400
E(GPa)
200
100
80
60
40
Graphite
Composites
Ceramics Polymers
/fibers
Semicond
Diamond
Tungsten
Molybdenum
Steel, Ni
Tantalum
Platinum
Cu alloys
Zinc, Ti
Silver, Gold
Aluminum
Magnesium,
Tin
Si carbide
Al oxide
Si nitride
Carbon fibers only
CFRE(|| fibers)*
<111>
Si crystal
Aramid fibers only
<100>
AFRE(|| fibers)*
Glass -soda
Glass fibers only
GFRE(|| fibers)*
Concrete
109 Pa
GFRE*
20
10
8
6
4
2
1
0.8
0.6
0.4
0.2
CFRE*
GFRE( fibers)*
Graphite
Polyester
PET
PS
PC
CFRE( fibers) *
AFRE( fibers) *
Epoxy only
PP
HDPE
PTFE
LDPE
Wood(
grain)
Based on data in Table B2,
Callister 7e.
Composite data based on
reinforced epoxy with 60 vol%
of aligned
carbon (CFRE),
aramid (AFRE), or
glass (GFRE)
fibers.
Useful Linear Elastic Relationships
• Simple tension:
d = FL o d = -n Fw o
L
EA o
EA o
F
a=
wo
2ML o
pr o4 G
M = moment
a = angle of twist
d/2
Ao
dL /2
• Simple torsion:
Lo
Lo
2ro
• Material, geometric, and loading parameters all
contribute to deflection.
• Larger elastic moduli minimize elastic deflection.
Resilience, Ur
• Ability of a material to store (elastic) energy
– Energy stored best in elastic region
Ur =
ey
0
sde
If we assume a linear
stress-strain curve this
simplifies to
1
Ur @ sy e y
2
Adapted from Fig. 6.15,
Callister 7e.
Plastic (Permanent) Deformation
(at lower temperatures, i.e. T < Tmelt/3)
• Simple tension test:
Elastic+Plastic
at larger stress
engineering stress, s
Elastic
initially
permanent (plastic)
after load is removed
ep
engineering strain, e
plastic strain
Adapted from Fig. 6.10 (a),
Callister 7e.
Yield Strength, sy
• Stress at which noticeable plastic deformation has
occurred.
when ep  0.002
tensile stress, s
sy
sy = yield strength
Note: for 2 inch sample
e = 0.002 = z/z
 z = 0.004 in
engineering strain, e
ep = 0.002
Adapted from Fig. 6.10 (a),
Callister 7e.
Tensile properties
Yielding Strength
Most structure operate in elastic region, therefore need to know when it ends
Yield strength
-- Generally quoted
Proportional
Limit
Proof stress
Some steels (lo-C)
Yield Strength : Comparison
Metals/
Alloys
Graphite/
Ceramics/
Semicond
Polymers
Composites/
fibers
2000
200
Al (6061) ag
Steel (1020) hr
Ti (pure) a
Ta (pure)
Cu (71500) hr
100
70
60
50
40
Al (6061) a
30
20
10
Tin (pure)
¨
dry
PC
Nylon 6,6
PET
PVC humid
PP
HDPE
LDPE
Hard to measure,
300
in ceramic matrix and epoxy matrix composites, since
in tension, fracture usually occurs before yield.
700
600
500
400
Ti (5Al-2.5Sn) a
W (pure)
Cu (71500) cw
Mo (pure)
Steel (4140) a
Steel (1020) cd
since in tension, fracture usually occurs before yield.
1000
Hard to measure ,
Yield strength, sy (MPa)
Steel (4140) qt
Room T values
Based on data in Table B4,
Callister 7e.
a = annealed
hr = hot rolled
ag = aged
cd = cold drawn
cw = cold worked
qt = quenched & tempered
Tensile Strength, TS
• TS is Maximum stress on engineering stress-strain curve.
Adapted from Fig. 6.11,
Callister 7e.
TS
F = fracture or
ultimate
strength
engineering
stress
sy
Typical response of a metal
Neck – acts
as stress
concentrator
strain
engineering strain
• Metals: occurs when noticeable necking starts.
• Polymers: occurs when polymer backbone chains are
aligned and about to break.
Tensile Strength : Comparison
Metals/
Alloys
Tensile strength, TS (MPa)
5000
3000
2000
1000
300
200
100
40
30
Graphite/
Ceramics/
Semicond
Polymers
C fibers
Aramid fib
E-glass fib
Steel (4140) qt
AFRE(|| fiber)
GFRE(|| fiber)
CFRE(|| fiber)
Diamond
W (pure)
Ti (5Al-2.5Sn)aa
Steel (4140)
Si nitride
Cu (71500) cw
Cu (71500) hr
Al oxide
Steel (1020)
ag
Al (6061) a
Ti (pure)
Ta (pure)
Al (6061) a
Si crystal
<100>
Glass-soda
Concrete
Room Temp. values
Nylon 6,6
PC PET
PVC
PP
HDPE
20
Composites/
fibers
Graphite
wood(|| fiber)
GFRE( fiber)
CFRE( fiber)
AFRE( fiber)
LDPE
10
wood (
1
fiber)
Based on data in Table B4,
Callister 7e.
a = annealed
hr = hot rolled
ag = aged
cd = cold drawn
cw = cold worked
qt = quenched & tempered
AFRE, GFRE, & CFRE =
aramid, glass, & carbon
fiber-reinforced epoxy
composites, with 60 vol%
fibers.
Ductility
• Plastic tensile strain at failure:
Lf - Lo
x 100
%EL =
Lo
smaller %EL
Engineering
tensile
stress, s
larger %EL
Lo
Ao
Af
Adapted from Fig. 6.13,
Callister 7e.
Engineering tensile strain, e
• Another ductility measure:
%RA =
Ao - Af
x 100
Ao
Lf
Lets Try Problem 6.28 (text)
GIVENS:
Load (N)
len. (mm)
len. (m)
D(l)
0
50.8
0.0508
0
12700
50.825
0.050825
2.5E-05
25400
50.851
0.050851
5.1E-05
38100
50.876
0.050876
7.6E-05
50800
50.902
0.050902
0.000102
76200
50.952
0.050952
0.000152
89100
51.003
0.051003
0.000203
92700
51.054
0.051054
0.000254
102500
51.181
0.051181
0.000381
107800
51.308
0.051308
0.000508
119400
51.562
0.051562
0.000762
128300
51.816
0.051816
0.001016
149700
52.832
0.052832
0.002032
159000
53.848
0.053848
0.003048
160400
54.356
0.054356
0.003556
159500
54.864
0.054864
0.004064
151500
55.88
0.05588
0.00508
124700
56.642
0.056642
0.005842
Leads to the following computed
Stress/Strains:
e stress (Pa)
e str (MPa)
e. strain
0
0
0
98694715.7
98.694716
0.000492
197389431
197.38943
0.001004
296084147
296.08415
0.001496
394778863
394.77886
0.002008
592168294
592.16829
0.002992
A0 use m 2 if F in Newtons; in 2 if F in lb f
692417257
692.41726
0.003996
results in Pa (MPa) or psi (ksi)
720393712
720.39371
0.005
and
796551839
796.55184
0.0075
837739398
837.7394
0.01
e = l l
927885752
927.88575
0.015
997049766
997.04977
0.02
1163354247
1163.3542
0.04
1235626755
1235.6268
0.06
1246506488
1246.5065
0.07
1239512374
1239.5124
0.08
1177342475
1177.3425
0.1
969073311
969.07331
0.115
s =FA
0
0
Leads to the Eng. Stress/Strain Curve:
Engineering Stress Strain
1400
T. Str.  1245 MPa
1200
F. Str  970 MPa
Stress (MPa)
1000
Y. Str.  742 MPa
800
%el  11.5%
Magenta Line Model:
s = m + Ee
600
m = -.002* E
e = .0021 to .0065
400
E  195 GPa
(by regression)
200
0
0
0.02
0.04
0.06
0.08
Strain (m/m)
0.1
0.12
0.14
TOUGHNESS
Is a measure of the ability of a material to absorb energy up to fracture
High toughness = High yield strength and ductility
Important Factors in determining Toughness:
1. Specimen Geometry & 2. Method of load application
Dynamic (high strain rate) loading condition (Impact test)
1. Specimen with notch- Notch toughness
2. Specimen with crack- Fracture toughness
Static (low strain rate) loading condition (tensile stress-strain test)
1. Area under stress vs strain curve up to the point of fracture.
Toughness
• Energy to break a unit volume of material
• Approximate by the area under the stress-strain
curve.
Engineering
tensile
stress, s
small toughness (ceramics)
large toughness (metals)
very small toughness
(unreinforced polymers)
Adapted from Fig. 6.13,
Callister 7e.
Engineering tensile strain,
Brittle fracture: elastic energy
Ductile fracture: elastic + plastic energy
e
Elastic Strain Recovery – After Plastic
Deformation
It is an important factor
in forming products
(especially sheet metal
and spring making)
Adapted from Fig. 6.17,
Callister 7e.
True Stress & Strain
Note: Stressed Area changes when sample is
deformed (stretched)
sT = F Ai
• True stress
sT = s1 + e 
• True Strain
eT = ln i  o 
eT = ln1 + e 
Adapted from Fig. 6.16,
Callister 7e.
Strain Hardening
• An increase in sy due to continuing plastic deformation.
s
large Strain hardening
sy
1
sy
small Strain hardening
0
e
• Curve fit to the stress-strain response:
 
sT = K eT
“true” stress (F/Ai)
n
hardening exponent:
n = 0.15 (some steels)
n = 0.5 (some coppers)
“true” strain: ln(Li /Lo)
Pr 6.28 – True Properties
T. Stress
T. Strain
0
0
98.74328592
0.000492
197.5875979
0.001003
296.5271076
0.001495
395.571529
0.002006
593.9401363
0.002988
695.1842003
0.003988
723.9956807
0.004988
802.525978
0.007472
846.1167917
0.00995
941.8040385
0.014889
1016.990761
0.019803
1209.888417
0.039221
1309.764361
0.058269
1333.761942
0.067659
1338.673364
0.076961
1295.076722
0.09531
1080.516741
0.108854
Necking Began
We Compute sT = KeTn to complete our
True Stress True Strain plot (plastic
data to necking)
• Take Logs of both sT and eT
• Regress the values from Yielding to
Necking
• Gives a value for n (slope of line) and K
(its sT when eT=1)
• Plot as a line beyond necking start
Stress Strain Plot w/ True Values
Engineering Stress Strain
& True Stress Stain
1800
n  0.242
K  2617 MPa
1600
1400
Stress (MPa)
1200
1000
800
600
400
200
0
0
0.02
0.04
0.06
0.08
Strain (m/m)
0.1
0.12
0.14
Variability in Material Properties
Critical properties depend largely on sample flaws
(defects, etc.). Most can exhibit Large sample to
sample variability.
• Real (reported) Values, thus, are Statistical
measures usually mean values.
n
– Mean
– Standard Deviation
 xn
x=
n
2
n
x i - x  

s=
 n -1 


1
2
where n is the number of data points (tests) that are performed
Design or Safety Factors
• Design uncertainties mean we do not push the limit!
• Typically as engineering designers, we introduce a
Factor of safety, N
Often N is
sworking =
sy
N
between
1.5 and 4
• Example: Calculate a diameter, d, to ensure that yield does
not occur in the 1045 carbon steel rod below subjected to a
working load of 220,000 N. Use a factor of safety of 5.
d
sworking =
sy
N
1045 plain
carbon steel:
sy = 310 MPa
TS = 565 MPa
F = 220,000N
Lo
Solving:
s working
s
= Y
N
=

310 N
m2

5
s working = F A = 220000 N
2
0
pD
220000 N

2
pD 4
=
D 2 = 220000  4  5
D  4.52 x10
2
D  6.72 x10
-3
-2
m

310 MN
m2
4

310 106  p
5

2
m  D = 6.72 cm
m2
Hardness
• Resistance to permanently (plastically) indenting the surface of a
product.
• Large hardness means:
--resistance to plastic deformation or cracking in compression.
--better wear properties.
apply known force
measure size
of indentation after
removing load
e.g.,
Hardened 10
mm sphere
D
most
plastics
brasses
Al alloys
Smaller indents
mean larger
hardness.
d
easy to machine
steels
file hard
cutting
tools
increasing hardness
nitrided
steels
diamond
Hardness: Common Measurement
Systems
Callister Table 6.5
Comparing
Hardness
Scales:
Inaccuracies in Rockwell (Brinell) hardness measurements may
occur due to:

An indentation is made too near a specimen edge.

Two indentations are made too close to one another.

Specimen thickness should be at least ten times the
indentation depth.

Allowance of at least three indentation diameters between the
center on one indentation and the specimen edge, or to the center of a
second indentation.

Testing of specimens stacked one on top of another is not
recommended.

Indentation should be made into a smooth flat surface.
Correlation Between Hardness and Tensile Strength
Both measures the resistance to plastic deformation of a material.
HB = Brinell Hardness
TS (psia) = 500 x HB
TS (MPa) = 3.45 x HB
Summary
• Stress and strain: These are size-independent
measures of load and displacement, respectively.
• Elastic behavior: This reversible behavior often
shows a linear relation between stress and strain.
To minimize deformation, select a material with a
large elastic modulus (E or G).
• Plastic behavior: This permanent deformation
behavior occurs when the tensile (or compressive)
uniaxial stress reaches sy.
• Toughness: The energy needed to break a unit
volume of material.
• Ductility: The plastic strain at failure.