Download 5.3 Notes

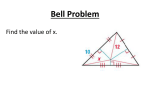
Warm-up:
1
Objectives
· Students will construct angle bisectors in a triangle
· Students will make and justify conjectures
· Students will use the properties of angle bisectors to solve problems
2
Construction # 2: Congruent Angles
Given:
Construct:
so that
Step 1: Draw a ray with endpoint S.
Step 2: With the compass point on point A,
draw an arc that intersects the sides of
. Label the points of intersection B and
C.
Step 3: With the same compass setting, put
the compass point on point S. Draw an arc
and label its point of intersection with the
ray as R.
Step 4: Open the compass to the length of
BC. Keeping the same compass point onR.
Draw an arc to locate point T.
Step 5: Draw
A
.
3
Parallel lines through a point
Given: line l and point R not on l
Construct: line m such that m // l
R
l
4
Practice:
Construct line t parallel to p through point X. Use perpendicular lines.
p
X
5
Construction # 6: Construct an Angle Bisector
Given:
Construct:
, the bisector of
Step 1: Put the compass point on vertexA.
Draw an arc that intersects the sides of
.
Label the points of intersection B and C.
A
Step 2: Put the compass point on C and draw
an arc. With the same compass setting, draw
an arc using point B. Be sure the arcs
intersect. Label the point where the two arcs
intersect as X.
Step 3: Draw
Draw Conclusions:
1. Why does this construction work?
2. What do you know about the two angles formed by the angle bisector?
3. Measure the distance from D to the sides of the angles. Make a conjecture
about the distance from any point on the angle bisector to the sides of the angle.
6
Construction # 8: Construct an Incenter
Step 1: Construct the angle bisectors of all
three vertex angles. Delete the arcs when
you finish each construction. The intersection
of the three angle bisectors is the incenter,I.
E
Step 2: Construct a circle whose center is I and
whose radius touches each side of the triangle.
D
F
7
8
9
10
11
Practice: Bisect the given angles.
B
A
C
12
SOL Prep What point is on the angle bisector of
a) X
b) Y
c) Z
d) Q
?
X
Z
Y
Q
A
13
Angle Bisectors in a triangle.
Construct the INCENTER.
B
A
C
14